 |
Астронет: "Физическая Энциклопедия"/Phys.Web.Ru Принцип Гюйгенса-Френеля http://www.astronet.ru/db/msg/1177410 |
 Принцип Гюйгенса-Френеля
Принцип Гюйгенса-Френеля11.06.2002 14:09 | "Физическая Энциклопедия"/Phys.Web.Ru
Гюйгенса-Френеля принцип - основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых.
Принцип Гюйгенса-Френеля является развитием принципа, который ввёл Х.Гюйгенс (Ch. Huygens) в 1678; в соответствии с последним каждый элемент поверхности, достигнутый в данный момент световой волной, является центром одной из элементарных волн, огибающая которых становится волновой поверхностью в следующий момент времени. При этом обратные элементарные волны во внимание не принимались. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. О.Ж.Френель (A.J.Fresnel) в 1815 дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса-Френеля и дифракционные явления. Г.Р.Кирхгоф (G.R.Kirchhoff) придал принципу Гюйгенса-Френеля строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа (см. Кирхгофа метод).
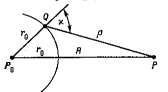 |
| Рис. 1. |
Согласно принципу Гюйгенса-Френеля, волновое возмущение в точке P (рис.1),
создаваемое источником P0, можно рассматривать
как результат интерференции вторичных элементарных волн, излучаемых каждым элементом
dS некоторой волновой поверхности S с радиусом r0.
Амплитуда
вторичных волн пропорциональна амплитуде первичной волны, приходящей в точку Q, площади
элемента dS и убывает с возрастанием угла ![]() между нормалью
к
поверхности S и направлением излучения вторичной волны на точку P. Амплитуда
EQ первичной волны в точке Q на поверхности S даётся выражением
между нормалью
к
поверхности S и направлением излучения вторичной волны на точку P. Амплитуда
EQ первичной волны в точке Q на поверхности S даётся выражением
![]() , где A
- амплитуда волны на расстоянии единицы длины от источника, k - волновой вектор,
, где A
- амплитуда волны на расстоянии единицы длины от источника, k - волновой вектор,
![]() - циклическая частота. Вклад в волновое возмущение в точке P,
вносимый элементом поверхности dS, запишется в виде
- циклическая частота. Вклад в волновое возмущение в точке P,
вносимый элементом поверхности dS, запишется в виде
| (1) |
где ![]() - расстояние от точки Q до P,
- расстояние от точки Q до P, ![]() - функция,
описывающая зависимость амплитуды вторичных волн от угла
- функция,
описывающая зависимость амплитуды вторичных волн от угла ![]() . Полное
поле
в точке наблюдения P представляется интегралом
. Полное
поле
в точке наблюдения P представляется интегралом
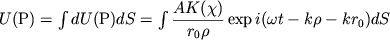 . . |
(2) |
Если за элемент поверхности взять площадь кольца, вырезаемого из волнового фронта
S двумя бесконечно близкими концентрическими сферами с центрами в точке наблюдения
P, и выразить
dS через приращение ![]() , то получим
, то получим
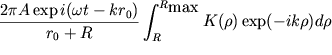 . . |
(3) |
Верхний предел интеграла Rmax=R+2r0. Функция
теперь рассматривается как функция от ![]() . Точное вычисление (3) невозможно
без знания
. Точное вычисление (3) невозможно
без знания ![]() , однако Френель дал метод приближённого его вычисления,
используя разбиение поверхности S на так называемые зоны Френеля.
Вид функции
, однако Френель дал метод приближённого его вычисления,
используя разбиение поверхности S на так называемые зоны Френеля.
Вид функции ![]() в принципе Гюйгенса-Френеля остается неопределенным,
но при
в принципе Гюйгенса-Френеля остается неопределенным,
но при ![]()
![]() ; множитель i означает,
что фазы вторичных волн отличаются на
; множитель i означает,
что фазы вторичных волн отличаются на ![]() от фазы первичной волны
в точке Q. Из математически точного определения принципа Гюйгенса-Френеля,
данного
Кирхгофом, следует и определение функции
от фазы первичной волны
в точке Q. Из математически точного определения принципа Гюйгенса-Френеля,
данного
Кирхгофом, следует и определение функции ![]() .
.
Строгое решение задач дифракции обычно связано с очень большими математическими трудностями, поэтому задачи, имеющие практический интерес, часто решаются приближенными методами с использованием принципа Гюйгенса-Френеля. Принцип Гюйгенса-Френеля позволяет описывать все оптические явления, относящиеся к распределению интенсивности света по разным направлениям (прямолинейное распространение света, отражение, преломление, двулучепреломление, дифракцию и т. д.). Приближённость решения с помощью принципа Гюйгенса-Френеля состоит в том, что при этом не рассматриваются реальные граничные условия электродинамики Максвелла. Например, при рассмотрении распространения волн через отверстия в экране амплитуда волны в точках, закрытых экраном, полагается равной нулю, а на отверстии - такой, как если бы экрана не было (т. е. допускается разрыв волнового поля).