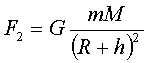 |
Астронет: Л. В. Жуков/РПГУ им. А.И. Герцена Современная астрономия и методика ее преподавания http://variable-stars.ru/db/msg/1177124/48.html |
| << Предыдущая |
Задачи с элементами небесной механики и методы их решения
Арюткина А.А.
Арзамасский государственный
педагогический институт им. А.П. Гайдара
Сила тяготения со стороны Земли, которая может быть выражена через ускорение свободного падения как F=mg, непостоянна и находится в зависимости от ряда факторов. Это нашло отражение в школьном курсе физики. Напомним, что сила гравитации, а, следовательно, и ускорение свободного падения являются функциями:
- высоты поднятия тела над Землёй,
- аномалии в строении земной поверхности,
- широты местонахождения тела на поверхности Земли, что вызвано натуральной сплюснутостью, и эффектом осевого вращения нашей планеты. (1).
Одна из простейших задач на расчет силы тяжести может быть сформулирована следующим образом:
Задача 1. Определить силу, с которой Земля притягивает к себе тело, находящееся от нее на высоте 630 км, если сила тяготения близ поверхности Земли известна и равна 600 H. Радиус Земли считать равным 6370 км.
|
Дано:
h=630 км. |
Решение: В соответствии с законом тяготения выражения силы тяжести для двух случаев могут быть записаны в скалярной форме: |
| F-? |
Их отношение позволит легко определить значение искомой величины
и после подстановки данных
В качестве примера можно привести определение силы тяжести на земном спутнике, Луне, на одной из планет-гигантов или их спутниках, либо на одном из астероидов, воспользовавшись при этом конкретными сведениями о величинах поперечников рассматриваемых объектов, плотностей и их масс.
Задача 2. С каким периодом должен вращаться космический корабль диаметром 6м., чтобы космонавт чувствовал себя как в поле тяготения Луны, находясь на ее поверхности. Известны отношения масс, радиусов Земли и Луны (81 и 11/3 соответственно). Ускорение свободного падения на поверхности Земли считать известным.
|
Дано: Mл=81 Mз. |
Решение: Во вращающемся космическом корабле возникает сила F, прижимающая космонавта в направлении от оси вращения к стенке корабля. Эта сила есть результат ускоренного движения системы и связана с центростремительным ускорением знаком минус F = -ma, |
| Т - ? |
где m - масса космонавта, a - центростремительное ускорение, равное w2r. Через диаметр выражение для F примет вид
В том случае, если космонавт находится в поле силы тяжести спутника Земли, последняя может быть представлена через ускорение свободного падения на поверхности Луны g'. F=mg'. Связывая два соотношения для силы F, будем иметь
В условии задачи известны отношения масс, радиусов планеты и спутника, а потому ускорение свободного падения на поверхности Луны найдется из отношения следующих выражений:
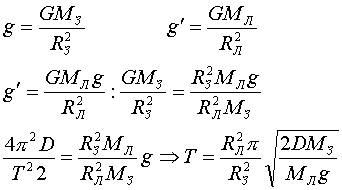
После подстановки данных
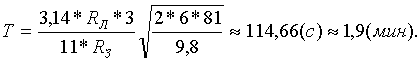
Задача 3. Астероид Церера (4) с средней плотностью вещества около 2500 кг/м3 имеет размер поперечника 770 км. Зная массу своего тела, определите с какой силой притягивает вас к своей поверхности Церера. Как долго смогли бы вы падать на поверхность планеты с высоты 10м. (сравните с временем падения на Земли при g=9,81 м/с2). Какую скорость, во-первых, необходимо сообщить телу на поверхности Цереры, и, во-вторых, вышло из поля гравитации планеты. (Цереру считать однородным шаром).
|
Дано: ρ=2500 кг/м3 |
Решение: Первых три вопроса не представляют трудности для их разрешения. Из закона тяготения следует, что
где M, R - масса и радиус астероида. |
| Р-? t-? V-? V-? |
Масса Цереры легко рассчитывается через плотность и объем сферического тела.
Следовательно
В результате подстановки числовых данных будем иметь
Если учесть массу человека, скажем, в 60 кг., то F=16,2 H. Считая ускорение свободного падения близ поверхности планеты постоянным, можно, применив формулу пути равнопеременного движения, определить время, за которое свободно падающее без начальной скорости тело пройдет расстояние 10 метров.
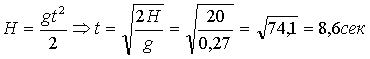
Оно, оказывается в 6,02 раза больше времени падения тела на поверхности Земли.
Третий и четвертый вопросы преследуют цель нахождения первой и второй космической скоростей, с приобретением которых тела становятся либо искусственными спутниками планет, либо выходят из поля гравитации планет. Определение космических скоростей - это второй тип задач, предлагаемых вниманию читателя.
С процессом нахождения первой космической скорости тело относительно Земли учащийся хорошо знаком из курса физики средней школы. С одной стороны, центростремительное ускорение, сообщаемое движущемуся по круговой орбите телу силой земного притяжения,
,
и с другой стороны,
,
где R - радиус Земли, а скорость
рассчитывается относительно поверхности
Земли. Эта скорость и есть первая
космическая.
Расписывая силу земного тяготения, будем иметь
С увеличением высоты тела над Землей круговая скорость уменьшается и тем значительнее, чем больше h.
После подстановки данных в формулу для первой космической скорости получаем хорошо знакомую цифру
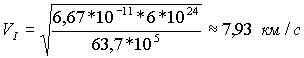
Для Цереры, в частности, первая космическая скорость примет значение:
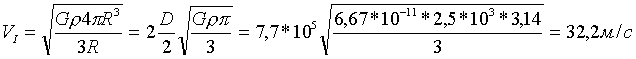
Определение скорости освобождения тела из поля гравитации планеты или звезды ведется с позиции интегрального метода исчисления, с которым старшеклассник и, более того, студент ВУЗа хорошо знаком.
Рассуждаем
следующим образом: кинетическая энергия,
которую следует сообщить телу у
поверхности Земли, должна полностью
расходоваться на работу по преодолению сил
земного тяготения
, где VII
- есть вторая космическая скорость.
Поскольку сила тяжести переменна и зависит от расстояния до планеты, то рассчитать работу этой силы можно, выделив очень малый участок пути (dr), на котором направление, а также величину силы можно считать постоянной. Тогда элементарная работа на малом участке перемещения примет вид dA=Fdr. А полная работа определяется путем интегрирования
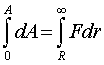
Пределы интегрирования выбраны с учетом того, что в начале пути тело находилось на поверхности Земли, а в конце ушло в бесконечность относительно поля земного тяготения.
Итак:
Подставив в выражение для кинетической энергии вместо работы А, будем иметь для второй космической скорости значение
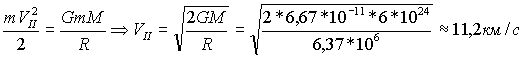
Относительно астероида Цереры вторая космическая скорость вычисляется согласно выражению:
Ввести определение скоростей космических объектов аналогичным образом можно, вкладывая в содержание задач несколько иной смысл.
Перечень предлагаемых задач может быть значительно расширен, и, естественно, в компетенции преподавателя видоизменить ассортимент как качественных, так и вычислительного характера примеров раздела небесной механики. Полагаем, что с привлечением рекомендуемого в данной работе типа задач существенно повысится интерес учащихся (студентов) к изучению темы "Всемирное тяготение" обязательных курсов физики, астрономии и факультативных курсов, спецкурсов в школе и ВУЗе, что приведет к интенсификации процесса усвоения материала.
| << Предыдущая |