 |
Астронет: В. В. Орлов/Коуровка Орбиты в звездных системах http://www.astronet.ru/db/msg/1176548/node3.html |
<< 1. Введение | Оглавление | 3. Орбиты в тройных системах >>
2. Орбиты звезд в галактических моделях
Многие галактики в первом приближении можно считать
ротационно-симметричными,
то есть обладающими осью симметрии и ортогональной
ей плоскостью симметрии.
В ротационно-симметричной системе
потенциал регулярного поля зависит только от двух координат -
расстояния ![]() от оси симметрии
и расстояния
от оси симметрии
и расстояния ![]() от плоскости симметрии:
от плоскости симметрии:
![]() .
В такой системе существуют два интеграла движения:
интеграл энергии
.
В такой системе существуют два интеграла движения:
интеграл энергии ![]() и интеграл площадей
и интеграл площадей ![]() .
.
Используя интеграл площадей ![]() ,
мы сводим задачу к двумерной.
Движение рассматривается
в сопутствующей (меридиональной) плоскости
в поле эффективного (приведенного) потенциала
,
мы сводим задачу к двумерной.
Движение рассматривается
в сопутствующей (меридиональной) плоскости
в поле эффективного (приведенного) потенциала
 |
(1) |
Сопутствующая плоскость вращается вместе со звездой вокруг оси симметрии. Уравнения движения частицы в этой плоскости имеют вид
 |
(2) |
Звезда в сопутствующей плоскости ![]() может двигаться в пределах
области возможных движений, где
может двигаться в пределах
области возможных движений, где
| (3) |
Из уравнений движения (2) можно получить уравнение для кривизны траектории
 |
(4) |
Здесь ![]() - угол между касательной к траектории и осью
- угол между касательной к траектории и осью ![]() ;
;
![]() и
и ![]() - направления вдоль касательной и нормали к траектории.
- направления вдоль касательной и нормали к траектории.
Угол ![]() описывает поле скоростей (поле направлений),
создаваемое витками траектории в сопутствующей плоскости.
Возможно описание свойств движения звезды в поле эффективного потенциала
с помощью поля направлений
(см. обзор Агекяна [1]).
описывает поле скоростей (поле направлений),
создаваемое витками траектории в сопутствующей плоскости.
Возможно описание свойств движения звезды в поле эффективного потенциала
с помощью поля направлений
(см. обзор Агекяна [1]).
В частности, было установлено, что в точках касания траекторией контура орбиты или контура складки поля направлений выполняется равенство
 |
(5) |
Это равенство позволяет наносить точки контуров орбиты и складок при движении вдоль траектории.
Рассмотрим поведение поля скоростей в окрестности неустойчивой периодической орбиты на примере известной модели Энона-Хейлеса [14] с приведенным потенциалом
 |
(6) |
В этом потенциале известно много периодических орбит.
Рассмотрим одну из них -
неустойчивую центральную периодическую орбиту
при
![]() с начальными условиями
с начальными условиями
| (7) |
На рис. 1 показана эволюция поля скоростей
по мере приближения к неустойчивой периодической орбите
при увеличении интеграла энергии.
При малых значениях ![]() орбита является оболочкообразной
и не имеет складок.
Затем появляются три складки,
которые постепенно разрастаются и перекрываются.
Далее на серединах контуров складок первого порядка
появляются складки второго порядка,
которые постепенно увеличиваются и вытягиваются
вдоль контуров складок первого порядка.
На углах складок второго порядка образуются
складки третьего порядка (рис. 2).
орбита является оболочкообразной
и не имеет складок.
Затем появляются три складки,
которые постепенно разрастаются и перекрываются.
Далее на серединах контуров складок первого порядка
появляются складки второго порядка,
которые постепенно увеличиваются и вытягиваются
вдоль контуров складок первого порядка.
На углах складок второго порядка образуются
складки третьего порядка (рис. 2).
Что происходит при дальнейшем приближении к неустойчивой периодической орбите, пока остается неясным. Численное моделирование показывает разрушение "складчатой" структуры и наступление стохастичности. Однако такой результат может быть обусловлен ошибками численного интегрирования.
После перехода через неустойчивый резонанс поле направлений восстанавливает регулярную форму. В зонах с большим числом неустойчивых периодических орбит поведение поля скоростей кажется стохастическим, однако в переходных зонах могут присутствовать элементы регулярности.
 |
Рис. 1. Эволюция структуры поля скоростей при изменении интеграла энергии: a) I=0.026, b) I=0.033, c) I=0.051, d) I=0.066, e) I=0.086, f) I=0.089. |
Теперь рассмотрим орбиты звезд в более реалистичных моделях, представляющих регулярное поле Галактики. На рис. 3 изображена орбита Солнца - типичной звезды галактического диска - в сопутствующей плоскости. Витки траектории заполняют ящик. В трехмерном пространстве орбита заполняет тор (бублик). Большинство звезд диска Галактики имеют ящикообразные орбиты. Исключение составляют траектории, попадающие в окрестности устойчивых периодических орбит (устойчивых резонансов). Тогда орбита является трубкообразной (рис. 4). Звезды гало могут иметь более экзотические орбиты (рис. 5).
Представляет интерес рассмотреть распределения элементов орбит звезд окрестности Солнца, поскольку эти распределения могут дать полезную информацию о процессе звездообразования в диске Галактики. Будем характеризовать орбиту каждой звезды двумя параметрами:
- эксцентриситет

(8)
- относительное максимальное удаление от плоскости симметрии

(9)
Здесь
![]() и
и ![]() -
максимальное и минимальное удаления звезды от оси
симметрии;
-
максимальное и минимальное удаления звезды от оси
симметрии;
![]() -
максимальное удаление от плоскости симметрии.
-
максимальное удаление от плоскости симметрии.
На рис. 6 и 7
представлены распределения
![]() и
и ![]() , построенные по данным о звездах
окрестности Солнца радиусом 25 парсек
из каталога Глизе и Ярайса [4].
Распределения несимметричны:
большинство орбит близки к круговым
и сильно сплюснуты к плоскости Галактики.
Это орбиты звезд диска.
Заметим однако, что распределения убывают
при
, построенные по данным о звездах
окрестности Солнца радиусом 25 парсек
из каталога Глизе и Ярайса [4].
Распределения несимметричны:
большинство орбит близки к круговым
и сильно сплюснуты к плоскости Галактики.
Это орбиты звезд диска.
Заметим однако, что распределения убывают
при
![]() и
и
![]() .
Этот факт может говорить о некотором спаде
процесса звездообразования в современную эпоху,
поскольку формирование звезд идет в облаках,
движущихся в Галактике по орбитам, близким к круговым,
и происходит "разогрев" диска за счет сближений звезд
с облаками газа.
Или просто Солнце сейчас находится вдали от областей
активного звездообразования.
.
Этот факт может говорить о некотором спаде
процесса звездообразования в современную эпоху,
поскольку формирование звезд идет в облаках,
движущихся в Галактике по орбитам, близким к круговым,
и происходит "разогрев" диска за счет сближений звезд
с облаками газа.
Или просто Солнце сейчас находится вдали от областей
активного звездообразования.
На распределениях ![]() и
и ![]() заметны
вторичные максимумы, которые могут свидетельствовать
о наличии периодов повышенного темпа звездообразования
в диске Галактики.
Однако эти максимумы не являются статистически значимыми,
поэтому делать какие-либо выводы
о наличии нескольких периодов усиленного звездообразования
в диске Галактики по этим данным пока преждевременно.
заметны
вторичные максимумы, которые могут свидетельствовать
о наличии периодов повышенного темпа звездообразования
в диске Галактики.
Однако эти максимумы не являются статистически значимыми,
поэтому делать какие-либо выводы
о наличии нескольких периодов усиленного звездообразования
в диске Галактики по этим данным пока преждевременно.
Исследуя орбиты близких звезд относительной солнечной орбиты,
мы можем найти звезды,
которые могли испытать в прошлом
или, возможно,
испытают в будущем сближение с Солнечной системой
в пределах внешнего облака Оорта,
то есть с минимальным расстоянием ![]() от Солнца менее
от Солнца менее
![]() астрономических единиц.
астрономических единиц.
Данные о таких звездах представлены в таблице. В таблице приведены номер звезды по каталогу Глизе и Ярайса [4], название звезды, ее спектральный тип, масса, минимальное расстояние между Солнцем и звездой, момент времени сближения по отношению к современной эпохе. Заметим, что из семи приведенных звезд шесть испытают сближение с Солнечной системой в будущем и лишь одна звезда - в прошлом (около 500000 лет тому назад). Интересно, что четыре сближения произойдут в течение ближайших 50000 лет.
Эти сближения могут вызвать обильные кометные ливни из внешней части облака Оорта в пределы планетной системы, что, в свою очередь, увеличивает вероятность столкновения с кометным ядром. Таким образом, кометные ливни могут приводить к экологическим катастрофам и массовым вымираниям организмов.
| Номер | Название | Масса, |
|||
| 82 | GJ 2005 | 0.18 | 154000 | 33000 | |
| 1844 | Gliese 445 | 0.27 | 197000 | 44000 | |
| 1973 | Gliese 474 | 4.0 | 54000 | 427000 | |
| 2317 | 1.8 | 186000 | 27000 | ||
| 2891 | Gliese 710 | 0.42 | 69000 | 1360000 | |
| 3706 | - | 1.0 | 112000 | -517000 | |
| 3742 | Gliese 905 | 0.40 | 195000 | 36000 | |
Еще один возможный фактор, приводящий к кометным ливням, - прохождения Солнечной системы через плоскость Галактики, где наблюдается повышенная концентрация молекулярных облаков. Воздействие молекулярных облаков на Солнечную систему может быть многогранным:
- 1) гравитационное возмущение на внешнюю часть облака Оорта;
- 2) насыщение дополнительной пылевой материей Солнечной системы;
- 3) дополнительный приток кометных ядер.
Подтверждение роли прохождений Солнца через галактическую плоскость в эволюции Земли - квазипериодичность массовых вымираний организмов и интенсивности импактных событий в истории Земли. Период около 30 миллионов лет сопоставим со средним интервалом времени между последовательными пересечениями галактической плоскости. Кстати, последнее прохождение имело место около 3 миллионов лет назад, а последнее массовое вымирание - около 11 миллионов лет назад.
Заметим, что три наиболее интенсивные вымирания (в том числе и вымирание динозавров около 65 миллионов лет назад) имели место вблизи апоцентра солнечной орбиты в Галактике (рис. 8). Недавно в этой области было обнаружено кольцо повышенной плотности молекулярного и атомарного водорода [9]. Возможно, вымирания были вызваны сближениями Солнечной системы с облаками из этого кольца.
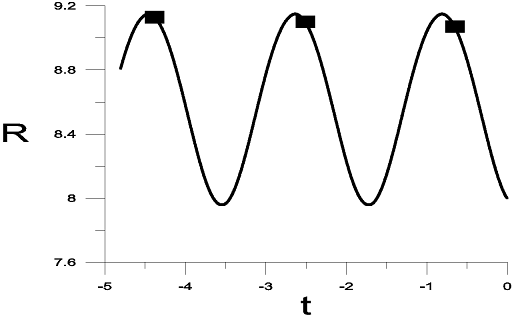 |
Рис. 8. Зависимость расстояния от Солнца до центра Галактики от времени (сотни миллионов лет) и эпохи массовых вымираний (квадратики) |
<< 1. Введение | Оглавление | 3. Орбиты в тройных системах >>





