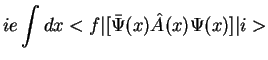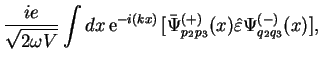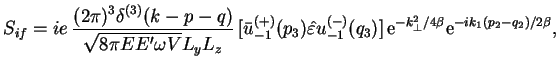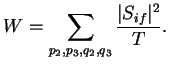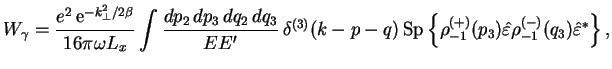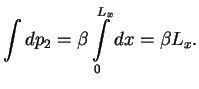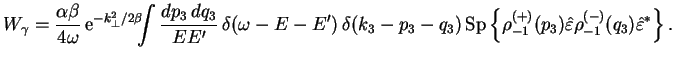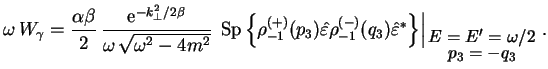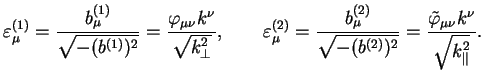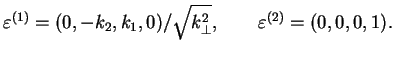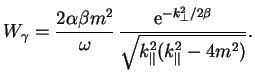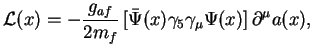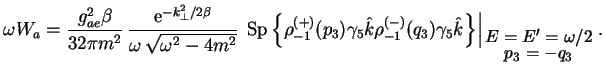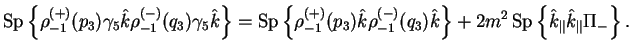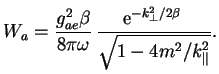|
Астронет: Л.А. Василевская, Н. В. Михеев, А.Я. Пархоменко Задания по квантовой теории поля
в сильном внешнем магнитном поле http://www.astronet.ru/db/msg/1176430/node3.html |
<< Вводные задания | Оглавление | Однопетлевые двухточечные процессы >>
Древесные процессы
(Задание 4, Задание 5)
Задание 4. Вычислить вероятность распада фотона на электрон-позитронную пару в сильном внешнем магнитном поле.
Решение. Распад фотона на электрон-позитронную пару, запрещенный в вакууме законом сохранения энергии-импульса, становится возможным в присутствии внешнего магнитного поля. Это связано с тем, что магнитное поле выступает в роли активной внешней среды, взаимодействие с которой приводит к изменению законов сохранения, а значит, и кинематики процесса.
Поскольку распад фотона анализируется в пределе сильного магнитного
поля
![]() , где
, где ![]() - масса электрона и
- масса электрона и
![]() - энергия фотона, то естественно волновые функции
электрона и позитрона выбрать в асимптотическом виде (3.2).
Перейдем теперь к вычислению
- энергия фотона, то естественно волновые функции
электрона и позитрона выбрать в асимптотическом виде (3.2).
Перейдем теперь к вычислению ![]() -матричного элемента процесса
-матричного элемента процесса
![]() ,
изображенного диаграммой на рис. 1.
,
изображенного диаграммой на рис. 1.
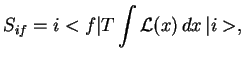 |
(4.1) |
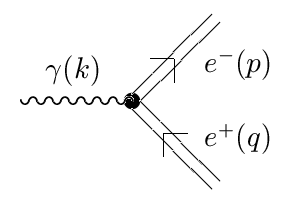 |
| Рис. 1. Диаграмма, описывающая распад фотона на электрон-позитронную пару во внешнем электромагнитном поле |
где
где
Интеграл по
где под трехмерной
Вероятность распада фотона в единицу времени равна квадрату модуля
![]() -матричного элемента, отнесенного к интервалу времени
-матричного элемента, отнесенного к интервалу времени ![]() ,
за который этот процесс произошел, и просуммированного по всевозможным
конечным состояниям:
,
за который этот процесс произошел, и просуммированного по всевозможным
конечным состояниям:
Как и в случае пропагатора электрона, при вычислении вероятности распада
где
Подставляя этот интеграл в (4.6) и вводя вместо квадрата заряда постоянную тонкой структуры
Две оставшиеся
Перейдем к вычислению шпура. Подставляя явный вид матриц
![]() из (3.6), для рассматриваемого шпура
получим следующий результат:
из (3.6), для рассматриваемого шпура
получим следующий результат:
где использованы свойства (1.15) шпуров
Выясним, фотоны какой поляризации имеют ненулевую вероятность распада
на электрон-позитронную пару. Для этого вспомним, что тензор напряженностей
внешнего электромагнитного поля позволяет построить удобный
базис (1.17) для такого рода анализа. При этом два
поляризационных состояния фотона, ортогональных к его волновому вектору
k, могут быть выбраны пропорциональными первым двум базисным
векторам
![]() и
и
![]() :
:
В выбранной нами системе отсчета (
Только 4-вектор "второй" фотонной поляризации имеет ненулевые составляющие в
Подстановка
![]() из (4.12) в выражение для
шпура (4.10) приводит к простому результату -
из (4.12) в выражение для
шпура (4.10) приводит к простому результату - ![]() .
Учитывая, что произведение энергии распадающегося фотона на вероятность
его распада есть лоренц-инвариантная величина, перейдем в произвольную
систему отсчета (
.
Учитывая, что произведение энергии распадающегося фотона на вероятность
его распада есть лоренц-инвариантная величина, перейдем в произвольную
систему отсчета (
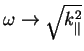 ) и для вероятности распада
) и для вероятности распада
![]() получим окончательный результат:
получим окончательный результат:
Задание 5. Вычислить вероятность распада аксиона на электрон-позитронную пару в сильном внешнем магнитном поле.
Решение. Аксион - это псевдоскалярная частица, введенная для решения проблемы CP-инвариантности сильных взаимодействий. В модели так называемого "невидимого" аксиона с прямой связью аксиона с обычными фермионами лагранжиан взаимодействия имеет вид:
где
Распад аксиона на электрон-позитронную пару, запрещенный в
вакууме законом сохранения энергии-импульса, становится возможным в
присутствии внешнего магнитного поля в полной аналогии с распадом фотона.
Легко увидеть, что ![]() -матричный элемент процесса, изображенного на
рис. 2,
-матричный элемент процесса, изображенного на
рис. 2,
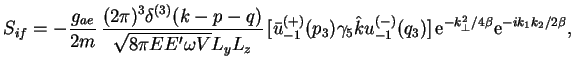 |
(5.2) |
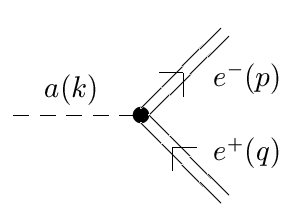 |
| Рис. 2. Диаграмма, описывающая распад аксиона на электрон-позитронную пару во внешнем электромагнитном поле в модели с прямой связью аксиона с электроном |
где
Вычислим шпур
Если учесть, что электрон и позитрон находятся на массовой поверхности (
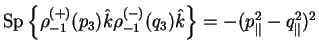 обращается в нуль, а второй -
обращается в нуль, а второй -
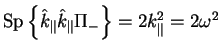 . Далее, возвращаясь в произвольную систему отсчета из системы,
где
. Далее, возвращаясь в произвольную систему отсчета из системы,
где
<< Вводные задания | Оглавление | Однопетлевые двухточечные процессы >>