 |
Астронет: СОЖ Преодоление дифракционного предела в оптике http://www.astronet.ru/db/msg/1176358/text1.html |
Преодоление дифракционного предела в оптике
М. Н. Либенсон
Санкт-Петербургский государственный институт точной механики и оптики (технический университет)СодержаниеВведение
Еще совсем недавно считалось, что предел возможному в оптике ставит фундаментальный рэлеевский критерий разрешения оптических приборов. Он заключается в том, что минимальный размер различимого объекта несколько меньше длины волны используемого света и принципиально ограничен дифракцией излучения. Однако в последнее время появилась и вызывает все больший интерес возможность изучения и формирования оптическими методами различных структур нанометровых размеров, которые во много раз меньше длины световой волны ![]() . Такая возможность возникла в связи с развитием ближнепольной оптики (БПО) - нового и чрезвычайно перспективного направления физической и прикладной оптики. С физической точки зрения она основана на присутствии в дальней зоне излучения вполне идентифицируемых следов взаимодействия света с микрообъектом, находящимся в ближнем световом поле, которое локализовано на расстояниях много меньших
. Такая возможность возникла в связи с развитием ближнепольной оптики (БПО) - нового и чрезвычайно перспективного направления физической и прикладной оптики. С физической точки зрения она основана на присутствии в дальней зоне излучения вполне идентифицируемых следов взаимодействия света с микрообъектом, находящимся в ближнем световом поле, которое локализовано на расстояниях много меньших ![]() . В техническом смысле БПО сочетает элементы обычной оптики и сканирующей зондовой микроскопии. Отличительным элементом ближнепольных приборов является оптический зонд (рис. 1), обычно представляющий собой заостренное оптическое волокно 1, наружная поверхность которого, за исключением вершины конуса, покрыта непрозрачным слоем металла 2.
. В техническом смысле БПО сочетает элементы обычной оптики и сканирующей зондовой микроскопии. Отличительным элементом ближнепольных приборов является оптический зонд (рис. 1), обычно представляющий собой заостренное оптическое волокно 1, наружная поверхность которого, за исключением вершины конуса, покрыта непрозрачным слоем металла 2.
Часть светового потока, распространяющегося по волокну, проходит через выходное сечение зонда как сквозь диафрагму в металлическом экране и достигает образца, расположенного в ближнем поле источника. Если расстояние z до поверхности образца и радиус a диафрагмы удовлетворяют условию ![]() , то размер светового пятна на образце близок к размеру диафрагмы. При перемещении зонда вдоль образца возможна реализация разрешения, не ограниченного дифракцией, или сверхразрешения.
, то размер светового пятна на образце близок к размеру диафрагмы. При перемещении зонда вдоль образца возможна реализация разрешения, не ограниченного дифракцией, или сверхразрешения.
Подобная идея была предложена еще в 1928 году Сингхом (E.H. Syngh), она намного опередила технические возможности своего времени и осталась практически не замеченной. Ее первое подтверждение было получено Эшем (E.A. Ash) в опытах с микроволнами в 1972 году. В начале 80-х годов группа исследователей из Цюрихской лаборатории фирмы IBM во главе с Дитером Полем (D.W. Pohl) проникла внутрь дифракционного предела и продемонстрировала разрешение ![]() /20 на приборе, работающем в видимом оптическом диапазоне и получившем название ближнепольного сканирующего оптического микроскопа (БСОМ).
/20 на приборе, работающем в видимом оптическом диапазоне и получившем название ближнепольного сканирующего оптического микроскопа (БСОМ). 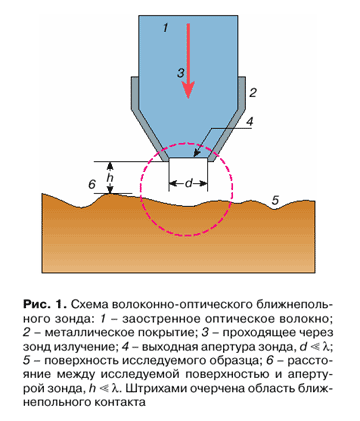 Чуть раньше в той же лаборатории был создан первый сканирующий туннельный микроскоп, принесший ей всемирную известность.
Чуть раньше в той же лаборатории был создан первый сканирующий туннельный микроскоп, принесший ей всемирную известность.
В отличие от туннельного и атомно-силового микроскопов, сразу завоевавших признание, БСОМ некоторое время оставался в тени. Уникальные возможности БСОМ были убедительно продемонстрированы лишь в начале 90-х годов, когда удалось решить две важные технические проблемы: существенно повысить энергетическую эффективность зондов и обеспечить надежный контроль расстояния между острием и образцом. В последние годы в десятках лабораторий успешно ведутся работы по использованию БСОМ при решении широкого круга задач физики поверхности, биологии, техники записи и считывания информации и др. С 1993 года в США ведется промышленный выпуск приборов БПО.
Ниже рассмотрена одна из простейших схем ближнепольного микроскопа, дано объяснение возможности получить сверхразрешение в оптике исходя из первых принципов, обсуждаются некоторые применения БПО. Фактически эту статью можно рассматривать как введение в ближнепольную оптику.
Ближнепольный микроскоп
К настоящему времени создано около 20 типов БСОМ, различающихся особенностями оптической схемы и функциональным назначением зонда. В зависимости от наличия или отсутствия диафрагмы на конце зонда их можно разбить на две основные группы: апертурные и безапертурные. Принцип действия апертурных БСОМ, составляющих преобладающее большинство современных приборов, поясняет приведенная на рис. 2 блок-схема микроскопа.
Луч лазера (обычно гелий-неонового или аргонового) через согласующий элемент попадает в заостренное металлизированное волокно и на выходе сужается до размеров диафрагмы. Взаимное перемещение острия и образца в трех измерениях x, y, z осуществляется с помощью пьезодвижителей. Прошедшие через образец или отраженные и рассеянные фотоны улавливаются одним из микрообъективов (2 или 1 соответственно, см. рис. 2) и направляются в регистрирующий прибор, обычно фотоумножитель. 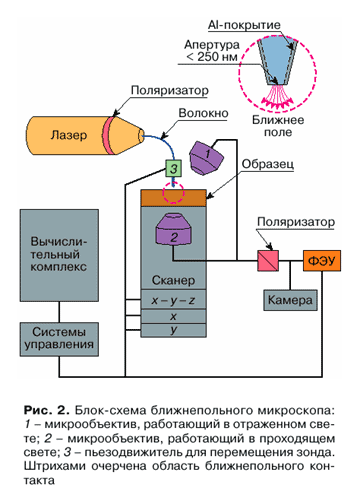 Такой микрообъектив, как правило, входит в схему обыкновенного оптического микроскопа, что позволяет осуществить выбор исследуемого участка и его привязку к более широкому полю. Приведенная на рис. 2 схема относится к приборам, работающим в режиме освещения (illumination mode). Широко распространены приборы, работающие в режиме сбора фотонов (collection mode), когда зонд переносит фотоны от образца, освещенного, например, через микрообъектив, к детектору. В комбинированном режиме (освещение / сбор) зонд выполняет одновременно обе функции.
Такой микрообъектив, как правило, входит в схему обыкновенного оптического микроскопа, что позволяет осуществить выбор исследуемого участка и его привязку к более широкому полю. Приведенная на рис. 2 схема относится к приборам, работающим в режиме освещения (illumination mode). Широко распространены приборы, работающие в режиме сбора фотонов (collection mode), когда зонд переносит фотоны от образца, освещенного, например, через микрообъектив, к детектору. В комбинированном режиме (освещение / сбор) зонд выполняет одновременно обе функции.
Чтобы установить острие на нужной высоте над образцом, во всех сканирующих зондовых микроскопах используют зависимость величины I регистрируемого сигнала от z. В большинстве типов БСОМ зависимость I(z) неоднозначна, поскольку наряду с ближнепольным сигналом I1 регистрируется также периодически изменяющийся с z сигнал I2 , вызванный интерференцией падающей и переотраженных в системе зонд-образец волн. Это затрудняет или делает полностью невозможным надежный контроль z по величине I = I1 + I2 при сближении острия с образцом. Лучшим решением проблемы является введение в БСОМ вспомогательных узлов, позволяющих им осуществлять также функции сканирующего туннельного или атомно-силового микроскопов, в которых определение z не вызывает существенных трудностей. В таких комбинированных приборах запись изображения осуществляется одновременно по двум каналам, один из которых воспроизводит рельеф поверхности, а другой - локальное распределение показателя преломления в тончайшем приповерхностном слое. Возможность различения оптического и топографического контрастов существенно упрощает интерпретацию изображения. Наибольшее распространение получил метод контроля z, основанный на изменении тангенциальной составляющей силы физического взаимодействия острия с образцом (shear force).
Разрешающая способность ближнепольных микроскопов
Основной характеристикой БСОМ является пространственное разрешение, которое в сильной степени зависит от условий освещения или в более общем случае - от наблюдения образца, структуры его поверхности и микрогеометрии зонда. Известно, что функция импульсного отклика дифракционно-ограниченной оптической системы описывается распределением Эри. Полуширина главного максимума распределения соответствует разрешению по Рэлею: ![]() , где
, где ![]() - апертурный угол. В пределе при
- апертурный угол. В пределе при ![]()
![]() . При прохождении света через малую диафрагму из-за рассеяния и геометрических ограничений происходит искажение и расширение
. При прохождении света через малую диафрагму из-за рассеяния и геометрических ограничений происходит искажение и расширение ![]() спектра переносимых пространственных частот, которое также описывается распределением Эри
спектра переносимых пространственных частот, которое также описывается распределением Эри ![]() . В результате при
. В результате при ![]() волновое поле непосредственно за диафрагмой содержит сколь угодно большие пространственные частоты и как следствие этого
волновое поле непосредственно за диафрагмой содержит сколь угодно большие пространственные частоты и как следствие этого ![]() . В реальной ситуации из-за конечной проницаемости металлического экрана (покрытия) минимальный эффективный радиус диафрагмы определяется глубиной проникновения света в металл или толщиной
. В реальной ситуации из-за конечной проницаемости металлического экрана (покрытия) минимальный эффективный радиус диафрагмы определяется глубиной проникновения света в металл или толщиной ![]() скин-слоя. С учетом этого ожидаемое предельное разрешение, например, для зонда с алюминиевым покрытием в видимом диапазоне спектра составляет
скин-слоя. С учетом этого ожидаемое предельное разрешение, например, для зонда с алюминиевым покрытием в видимом диапазоне спектра составляет ![]() нм, что соответствует лучшим экспериментальным результатам. Отсутствие физических ограничений размера вершины зонда в безапертурных БСОМ позволяет реализовать в них разрешение лучше 1 нм.
нм, что соответствует лучшим экспериментальным результатам. Отсутствие физических ограничений размера вершины зонда в безапертурных БСОМ позволяет реализовать в них разрешение лучше 1 нм.
Что такое ближнее поле
Критерий Рэлея является одной из иллюстраций принципа неопределенности Гейзенберга, согласно которому любая попытка повысить степень локализации или точность определения положения ![]() источника света приводит к возрастанию неопределенности
источника света приводит к возрастанию неопределенности ![]() сопряженного импульса фотонов. При рассеянии фотонов в максимальном диапазоне углов
сопряженного импульса фотонов. При рассеянии фотонов в максимальном диапазоне углов ![]() (
(![]() - постоянная Планка, kx - x-компонента волнового вектора k) и
- постоянная Планка, kx - x-компонента волнового вектора k) и ![]() . Возможность реализации разрешения
. Возможность реализации разрешения ![]() , казалось бы, противоречит одному из основных физических принципов. Следует, однако, иметь в виду, что соотношение неопределенности в самом общем виде относится к положению частицы в импульсно-координатном пространстве. Поэтому, ограничивая одну из компонент волнового вектора, оно позволяет варьировать другие. Можно принять, например,
, казалось бы, противоречит одному из основных физических принципов. Следует, однако, иметь в виду, что соотношение неопределенности в самом общем виде относится к положению частицы в импульсно-координатном пространстве. Поэтому, ограничивая одну из компонент волнового вектора, оно позволяет варьировать другие. Можно принять, например, ![]() ,
, ![]() , где
, где ![]() - вещественное положительное число. Тогда При
- вещественное положительное число. Тогда При ![]() область допустимых значений kx неограниченно растет, а
область допустимых значений kx неограниченно растет, а ![]() может быть сколь угодно малым.
может быть сколь угодно малым.
Мнимым kz соответствуют затухающие волны. Следовательно, при реализации субволнового разрешения антенна-зонд должна располагаться в пределах затухающего поля вблизи поверхности образца, то есть заведомо при ![]() .
.
Мы можем теперь уточнить понятие ближнего поля, ассоциируя его с областью существования затухающих и, следовательно, нерадиационных волн, амплитуда которых меняется с расстоянием z от границы раздела сред или малого рассеивающего объекта по закону ![]() , где g > 0. Величина g-1 характеризует глубину проникновения затухающей волны и по порядку соизмерима с размерами субволнового рассеивателя. В частности, для диафрагмы радиуса a в тонком проводящем экране
, где g > 0. Величина g-1 характеризует глубину проникновения затухающей волны и по порядку соизмерима с размерами субволнового рассеивателя. В частности, для диафрагмы радиуса a в тонком проводящем экране ![]() . Для поверхности со сложным рельефом величина g-1 определяется суммарным вкладом компонент спектра пространственных частот, причем m-я компонента с периодом
. Для поверхности со сложным рельефом величина g-1 определяется суммарным вкладом компонент спектра пространственных частот, причем m-я компонента с периодом ![]() обнаружима на расстоянии
обнаружима на расстоянии ![]() (В режиме сбора фотонов точность воспроизведения профиля поверхности возрастает с увеличением числа m компонент затухающего поля, участвующих в образовании изображения, а значит, с уменьшением z.) В дальнем поле при
(В режиме сбора фотонов точность воспроизведения профиля поверхности возрастает с увеличением числа m компонент затухающего поля, участвующих в образовании изображения, а значит, с уменьшением z.) В дальнем поле при ![]() присутствуют лишь распространяющиеся волны, к которым применимы законы и ограничения обычной оптики. Естественно, что они также вносят вклад в результирующее поле в ближней волновой зоне. Структуру ближнего поля могут определять также и различного рода поверхностные резонансные электромагнитные моды, возбуждаемые светом вблизи выходного сечения зонда (например, поверхностные поляритоны, о которых уже писалось в наших предыдущих статьях в "Соросовском Образовательном Журнале").
присутствуют лишь распространяющиеся волны, к которым применимы законы и ограничения обычной оптики. Естественно, что они также вносят вклад в результирующее поле в ближней волновой зоне. Структуру ближнего поля могут определять также и различного рода поверхностные резонансные электромагнитные моды, возбуждаемые светом вблизи выходного сечения зонда (например, поверхностные поляритоны, о которых уже писалось в наших предыдущих статьях в "Соросовском Образовательном Журнале").
Решение задачи о прохождении света через диафрагму радиусом ![]() в бесконечно тонком проводящем экране было впервые получено Г. Бёте. Оказалось, что диафрагма такого размера пропускает значительно меньше света, чем можно ожидать, экстраполируя результаты расчета при
в бесконечно тонком проводящем экране было впервые получено Г. Бёте. Оказалось, что диафрагма такого размера пропускает значительно меньше света, чем можно ожидать, экстраполируя результаты расчета при ![]() . В частности, сечение рассеяния
. В частности, сечение рассеяния ![]() неполяризованного света связано с величиной a и волновым числом
неполяризованного света связано с величиной a и волновым числом ![]() соотношением
соотношением
![]()
где ![]() - угол падения излучения.
- угол падения излучения.
Формула (1) помимо численного коэффициента отличается от используемой в расчетах по методу Кирхгофа дополнительным множителем ![]() . Различие вызвано тем, что значительная часть электромагнитной энергии переходит в нерадиационную форму, которая не может быть воспринята удаленным наблюдателем. С точки зрения такого наблюдателя, диафрагма рассеивает свет как пара взаимно перпендикулярных диполей: электрического, направленного вдоль оси диафрагмы, и магнитного, моменты которых равны соответственно
. Различие вызвано тем, что значительная часть электромагнитной энергии переходит в нерадиационную форму, которая не может быть воспринята удаленным наблюдателем. С точки зрения такого наблюдателя, диафрагма рассеивает свет как пара взаимно перпендикулярных диполей: электрического, направленного вдоль оси диафрагмы, и магнитного, моменты которых равны соответственно
![]()
![]()
где ![]() - электрический и магнитный векторы поля перед экраном. Чисто качественно формула (2) справедлива также и в случае, когда вместо диафрагмы выступает сфера радиуса a; при этом для количественного совпадения необходимо положить, что диэлектрическая проницаемость материала сферы
- электрический и магнитный векторы поля перед экраном. Чисто качественно формула (2) справедлива также и в случае, когда вместо диафрагмы выступает сфера радиуса a; при этом для количественного совпадения необходимо положить, что диэлектрическая проницаемость материала сферы ![]() .
.