Астронет: scientific.ru Двойной безнейтринный бета-распад: кажется, поспешили ... http://variable-stars.ru/db/msg/1176284

Двойной безнейтринный бета-распад: кажется, поспешили ...
10.04.2002 20:01 | scientific.ru

... Следующим пунктом у нас сообщение об обнаружении такого-то эффекта 2.5 в такой-то работе.     Ну, мы не верим в 2.5-эффекты, поэтому поехали дальше... Из обзора литературы на одном из семинаров.

Недавно вышел е-принт hep-ph/0201231, где заявляется, что найдено свидетельство существования двойного безнейтринного бета-распада. Авторы (H.V.Klapdor-Kleingrothaus, A.Deits, H.L. Harley, I.V.Krivosheina) относятся к довольно большой коллаборации Гейдельберг-Москва. Основная группа московской части коллаборации работает в ИАЭ им. Курчатова и возглавляется Спартаком Беляевым. Обычно, важные результаты, признаваемые всей коллаборацией, всей коллаборацией и подписываются. В данном случае стоит всего четыре подписи, что скорее всего говорит об отсутствии консенсуса у авторов эксперимента.

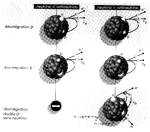
Эксперимент проводится глубоко под землей (ради снижения фона) в Гран-Сассо, в Италии. Измеряется двойной распад германия ⁷⁶Ge -> ⁷⁶Se + 2e^- + (2 ) (из-за проблемы с греческими символами во многих версиях Netscape обозначаем нейтрино через ). Такой распад (с двумя нейтрино) разрешен стандартной теорией слабых взаимодействий, хотя вероятность его сильно подавлена по сравнению с обычным бета-распадом. Если же существует несохранение лептонного числа, то распад может происходить без испускания двух нейтрино. Тогда суммарная энергия двух электронов строго фиксирована: 2039 кэВ, что можно было бы увидеть в спектре распада. Авторы утверждают, что они видят это.

Заявление достаточно серьезно, поскольку нарушение лептонного числа, хотя и не противоречит каким-то фундаментальным принципам, но должно было бы существенно повлиять на теорию. С этой точки зрения двойной безнейтринный бета-распад имеет тот же статус, что и осцилляции нейтрино - эффект, который давно ищут, и не исключено, что уже нашли.

Рис. Спектр распада 76Ge

В данном случае, однако, результат выглядит сомнительным. На рисунке показан спектр суммарной энергии двух электронов распада и кривая, показывающая вклад безнейтринного распада по результатам наилучшей подгонки данных. Уже сам рисунок неубедителен - ничего статистически значимого в районе ожидаемой линии на глаз не видно. Это при том, что обычно, когда есть даже статистически слабое указание на эффект, глаз его легко видит. В спектре видны слабозначимые линии в районе 2010 кэВ и 2050 кэВ - обе интерпретируются слабыми ядерными линиями ²¹⁴Bi, т.е. фоном. По заявлению авторов, статистическая значимость эффекта - 96.8 %, что соответствует 2.1 сигма. Для получения этой (вообще говоря малой) значимости авторам пришлось прибегнуть к дополнительным усилиям: ограничить интервал усреднения фона довольно узким участком вокруг искомой линии, иначе получается совсем плохо. Мотивировка: исключить из оценки фона известные линии, не имеющие отношения к бета-распаду. В результате, исключены все положительные флуктуации фона и оставлена депрессия, имеющая чисто статистическое происхождение. То есть фон занижен, соответственно, линия завышена.

Сказанного достаточно, чтобы отнестись к публикации крайне скептически. В феврале вышел е-принт большой группы авторов (C.E.Aalseth et al., hep-ex/0202018) с ее резкой критикой. В дополнение к вышесказанному, они обращают внимание на то, что упомянутые линии ²¹⁴Bi слишком слабы, чтобы наблюдаться как заметные пики в этом спектре. Скорее всего это лишь флуктуации фона и их не надо исключать при оценке, как сделали авторы. Но тогда результат рассыпается.

Теперь общее методическое замечание. Представьте, к вам обращается исследователь (честный и грамотный), заявляя, что он наблюдает какой-то эффект на уровне 2.5 сигма, и предлагает пари 10 к 1, что эффект подтвердится (т.е. если подтвердится, вы платите 1, если нет - он платит 10). Значимость 2.5 сигма примерно соответствует вероятности 0.01 получить такой эффект в результате статистической флуктуации и трактуется как 99% достоверность результата. На первый взгляд, в терминах математического ожидания, пари проигрышно для вас. На самом деле, если вы заранее (до измерений) не договорились с исследователем о каком точно эффекте пойдет речь, пари нужно немедленно заключать.

Дело в том, что количество эффектов, которые пытаются найти, огромно - наука широка. При этом для каждого эффекта могут быть разные наборы данных, разные методы их интерпретации и т.п. Значит, делается множество (допустим, несколько сотен в год) статистически независимых попыток найти какой-нибудь эффект. В каждой сотой попытке должна случайно выпадать флуктуация, имитирующая эффект на уровне 2.5 сигма. Таким образом в год должно появляться несколько сообщений о новых эффектах на уровне порядка 2.5 сигма, основанных на чисто статистических флуктуациях. Природа же более скупа на настоящие новые эффекты. Потому множество (конкретных оценок никто не проводил, но возможно и большинство) заявленных эффектов невысокого уровня значимости не подтверждаются.

Но любой малозначимый эффект, включая обсуждаемый, может оказаться настоящим. Поэтому, сообщения типа "есть малозначимое указание на такой-то важный эффект, к этому стоит присмотреться и набрать большую статистику" - вполне оправданы. Проблема в том, что часто авторы к тому же завышают значимость эффекта, именно это и вызвало критику данной статьи.

Б.Штерн