Астронет: СОЖ Обычные и необычные фазовые переходы http://variable-stars.ru/db/msg/1175819/page1.html

Обычные и необычные фазовые переходы

А. М. Скворцов (Санкт-Петербургский химико-фармацевтический институт)
Опубликовано в Соросовском образовательном журнале, N 8, 1996 г. Содержание

---

Классификация фазовых переходов

Согласно классификации Эренфеста, существует два типа фазовых переходов - первого и второго рода [Эткинс П. ,1980]. Обычные фазовые переходы, подобные кипению, плавлению или возгонке, сопровождаются скачкообразными изменениями внутренней энергии и объема (поглощением или выделением скрытого тепла перехода). Поскольку энергия и объем являются первыми производными от свободной энергии по температуре и давлению, то при этих фазовых переходах первые производные свободной энергии являются разрывной функцией. Это послужило основанием назвать такие превращения фазовыми переходами первого рода.

Переходы первого рода характеризуются бесконечно большим возрастанием теплоемкости в очень узкой области вокруг точки перехода. Физическая причина этого состоит в том, что добавление теплоты к системе в точке фазового перехода не повышает температуру системы, а расходуется на перестройку системы. В качестве примера на рисунке 1 показана температурная зависимость свободной энергии F, приходящейся на одну молекулу кристалла, при его превращении в пар. Верхняя ветвь отвечает кристаллическому состоянию, а нижняя ветвь представляет свободную энергию парообразной фазы. При низких температурах свободная энергия кристалла меньше, чем пара, и, следовательно, кристаллическое состояние выгоднее. При высоких температурах, наоборот, выгоднее существование парообразного состояния. Штриховыми линиями показаны области метастабильных, термодинамически неустойчивых состояний системы.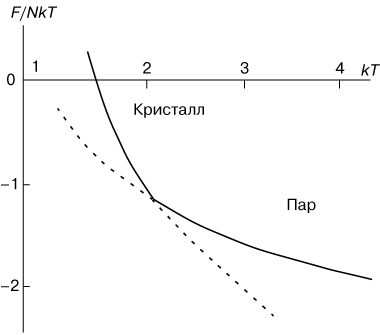

Рис. 1. Температурная зависимость свободной энергии F при фазовом переходе первого рода "пар-кристалл".

Поведение внутренней энергии системы, приходящейся на одну молекулу, изображено на рисунке 2. Нижняя ветвь относится к кристаллическому состоянию, а верхняя к парообразному. Скачок энергии в точке перехода представляет собой поглощаемую скрытую теплоту. Соответственно теплоемкость в точке фазового перехода первого рода имеет "всплеск".

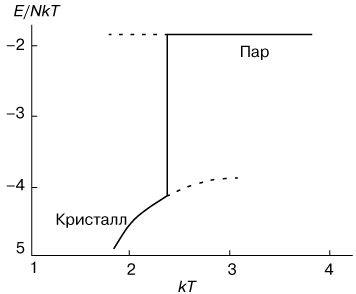Рис. 2. Изменение энергии E в зависимости от температуры T при фазовом переходе первого рода "пар-кристалл".

При теоретическом описании фазовых переходов первого рода каждую из фаз обычно описывают отдельно. Так, кристаллическую ветвь рассматривают, пользуясь моделью идеального кристалла, то есть предполагая регулярное расположение всех атомов. Парообразную же ветвь получают, используя модель идеального газа, предполагающую полный беспорядок в системе. Зависимости, полученные для различных моделей, накладывают друг на друга и исследуют, какая из возможностей реализуется в данных условиях. Получить описание фазового перехода первого рода, одновременно учитывая все состояния системы, до настоящего времени не удается из-за огромных математических трудностей.

При переходах второго рода внутренняя энергия вещества и его объем не изменяются в точке перехода и, следовательно, не происходит выделения или поглощения скрытой теплоты. Однако свободная энергия системы при фазовых переходах второго рода имеет некоторую особенность, которая проявляется в том, что вторые производные - теплоемкость и сжимаемость - становятся бесконечными. Выявление характера этой особенности - одна из наиболее трудных задач статистической физики. Существует всего несколько систем, для которых эта особенность была выяснена. Одной из таких систем является двумерная модель Изинга (модель двумерного ферромагнетика), рассмотренная Л. Онсагером [Ландау Л.Д., Лифшиц Е.М.,1976 ]. Изменение энергии ферромагнетика в двумерной модели Изинга происходит хотя и резко, но без скачков (рис. 3). При этом теплоемкость системы обращается в бесконечность по логарифмическому закону:

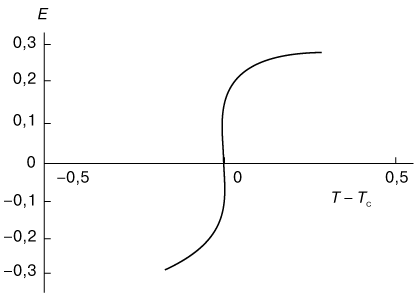Рис. 3. Изменение энергии E в зависимости от температуры T при фазовом переходе второго рода в двумерной модели Изинга.

.

(1)

Ход теплоемкости показан на рисунке 4. Форма кривой теплоемкости напоминает греческую букву , поэтому такие переходы иногда называют -переходами. Быстрый, но непрерывный подъем теплоемкости показывает, что система начинает процесс своей реорганизации задолго до достижения точки перехода.

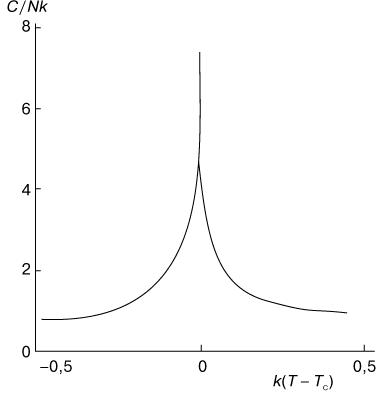Рис. 4. Ход теплоемкости C в зависимости от температуры T при фазовом переходе второго рода в двумерной модели Изинга.

Фазовые переходы с точки зрения теории Ландау

Глубокий анализ проблемы фазовых переходов был сделан Л.Д. Ландау [Ландау Л.Д., Лифшиц Е.М.,1976 ]. Согласно теории Ландау, при фазовых переходах первого рода функция распределения по энергии или плотности системы должна быть бимодальной, то есть иметь два максимума. Наиболее высокий максимум отвечает наиболее выгодному, стабильному, состоянию системы, а второй максимум соответствует менее выгодному, метастабильному, состоянию. В самой точке перехода высоты максимумов становятся одинаковыми и система может одновременно сосуществовать в обоих состояниях. При фазовых переходах второго рода функция распределения всегда имеет только один максимум, который расширяется в точке перехода. Соответственно при переходах второго рода метастабильных состояний в принципе не существует.

К сожалению, имеется очень мало систем, позволяющих провести строгое статистическое рассмотрение и проверить теорию Ландау. Однако, используя компьютеры, удалось смоделировать фазовые переходы газ-жидкость. Оказалось, что в точке фазового перехода первого рода распределение плотности действительно бимодально. При этом чем больше число частиц в системе, тем выше игуже пики на бимодальной кривой. Для очень большой системы область сосуществования двух фаз практически исчезает и при каждом значении внешних параметров - температуры и давления - мы наблюдаем только одну фазу, а сам фазовый переход происходит скачкообразно в чрезвычайно узкой области изменения температуры. С другой стороны, в точке фазового перехода второго рода, при так называемых критических условиях функция распределения плотности расширяется, но всегда имеет только один максимум, как и предполагалось в теории Ландау. Наличие или отсутствие бимодальности у функции распределения служит важным критерием, позволяющим определить род перехода. Обычно речь идет о функциях распределения по энергии системы или по ее плотности, или же по другому важному параметру, который называют параметром порядка системы. В последние годы было обнаружено, что существуют системы, способные совершать необычные фазовые превращения. Их необычность состоит в том, что они обладают характерными чертами фазовых переходов первого и второго родов одновременно. Такие переходы свойственны молекулам полимеров. В качестве примера мы рассмотрим переход, претерпеваемый адсорбированной полимерной цепью при ее отрывании от поверхности постоянной силой. Такая ситуация реализуется при внешних воздействиях на частицы полимерного клея, скрепляющего разные поверхности. Поэтому рассматриваемая задача имеет важное практическое значение для адгезии полимеров. Чтобы понять суть явления, достаточно рассмотреть упрощенную модель "липкой ленты".

Назад | Вперед