Л.А.Блюменфельд (
МГУ им. М.В.Ломоносова)
Опубликовано в
Соросовском образовательном журнале,
N 7, 1996 г.
Содержание
За 20 лет до появления работ Шеннона анализом информации занимался венгерский физик Сциллард
[Szillard L., 1929] в связи с решением одного термодинамического парадокса, предложенного Максвеллом еще в прошлом веке
[Maxwell J.C., 1971]. Смысл
парадокса Максвелла заключается в следующем (рис. 1). Изолированная система, состоящая из разделенного на две части резервуара с газом и с дверцей в перегородке, содержит также "
демона" (существо или автомат), наделенного способностью отличать быстрые молекулы от медленных. Демон открывает дверцу только в том случае, если к ней справа подлетает быстрая молекула. Поэтому газ в левой части резервуара будет нагреваться, а в правой - остывать. Таким образом, в изолированной системе тепло будет переходить от холодного тела к горячему с понижением
энтропии системы в противоречии со
вторым законом термодинамики.
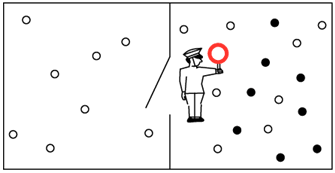 |
| Рис. 1. Демон Максвелла. |
Сциллард
[Szillard L., 1929], рассмотрев один из упрощенных вариантов
парадокса Максвелла, обратил внимание на необходимость получения информации о молекулах и открыл связь между информацией и
термодинамическими характеристиками. В дальнейшем решение парадокса Максвелла было предложено многими авторами (см., например,
[Бриллюен Л., 1960]). Смысл всех решений заключается в следующем: информацию нельзя получать бесплатно. За нее приходится платить энергией, в результате чего энтропия системы повышается на величину, по крайней мере равную ее понижению за счет полученной информации.
Пусть задано
макроскопическое состояние некоторой системы, то есть с определенной степенью точности указаны значения таких параметров, как объем, давление, температура, химический состав и т.п. Каждому макросостоянию системы соответствует набор микросостояний. В
микросостоянии прецизированы (точно заданы) состояния всех частиц, входящих в систему. Для любой макросистемы при температуре выше абсолютного нуля число микросостояний
W, соответствующих данному макросостоянию, огромно.
W называется
статистическим весом или
термодинамической вероятностью данного макросостояния. Согласно основному постулату статистической физики, все
W микросостояний, соответствующие одному макросостоянию, имеют одинаковую априорную вероятность. Знать микросостояние системы - значит знать о системе все!
Величина
W непосредственно связана с энтропией. По
формуле Планка-Больцмана
 , , | (3) |
где размерная
постоянная Больцмана k = 1,38*10
-16 эрг/град или 3,31*10
-24 эе (эе - энтропийная единица, 1 эе = 1 кал/град). Рассчитаем, какое количество информации надо получить о системе, находящейся в данном макросостоянии, чтобы однозначно определить ее микросостояние. Иначе говоря, какого количества информации недостает для полного описания системы в заданном макросостоянии?
Пусть микросостояние определено путем измерений или расчетов (на самом деле сделать это нельзя). До определения вероятность того, что макроскопическая система находилась именно в этом микросостоянии, была равна 1/
W, а после определения стала равной единице. Полученное количество информации
 | (4) |
Формулы (3) и (4) совпадают с точностью до постоянного размерного множителя. Величины
I и
S существенно идентичны. Ситуация здесь та же, что и для соотношения между массой и энергией:
E =
mc2, где роль размерного множителя играет
с2. Аналогична ситуация и в случае соотношения между частотой и энергией кванта света, где размерным множителем является
постоянная Планка:

.
Энтропия системы в данном макросостоянии есть количество информации, недостающее до ее полного описания. Чтобы перейти от количества информации в битах к энтропии в энтропийных единицах, необходимо перейти от логарифма при основании 2 к натуральному логарифму и умножить на
k:
 | (5) |
Назад | Вперед

