Astronet Астронет:  Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page3.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Метод векторных диаграмм.

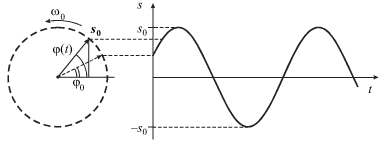
Гармонические колебания (1.7) допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой $\omega _{0}$ можно поставить в соответствие вращающийся с угловой скоростью $\omega _{0}$ вектор, длина которого равна амплитуде $s_{0},$ а его начальное (стартовое) положение задается углом $\varphi _{0},$ совпадающим с начальной фазой (рис. 1.5).

Рис. 1.5.

Вертикальная проекция вектора ${\displaystyle \bf s_{0}}$ изменяется со временем: $s(t) = s_{0} \sin \varphi (t).$ Мгновенное положение вектора ${\displaystyle \bf s_{0}}$ определяется углом $\varphi (t),$ который называется фазой и равен:

$ \varphi (t) = \omega _{0} t + \varphi _{0} . $(1.18)

При угловой скорости (круговой частоте) $\omega _{0}$ вектор совершает $\nu _{0} = \omega _{0} / 2\pi$ оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла $2\pi$ к угловой скорости $\omega _{0} :\; T = 2\pi / \omega _{0} .$

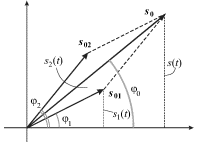
С помощью векторных диаграмм легко осуществить сложение гармонических колебаний. Так, если необходимо сложить два гармонических колебания с одинаковыми частотами

$ s(t) = s_{1} (t) + s_{2} (t) = s_{01} \sin (\omega _{0} t + \varphi _{1} ) + s_{02} \sin (\omega _{0} t + \varphi _{2} ) = s_{0} \sin (\omega _{0} t + \varphi _{0} ), $

то амплитуду $s_{0}$ и начальную фазу $\varphi _{0}$ суммарного колебания $s(t)$ с той же частотой $\omega _{0}$ можно легко рассчитать из рис. 1.6а, на котором графически изображена операция сложения векторов ${\displaystyle \bf s_{0}} = {\displaystyle \bf s_{01}} + {\displaystyle \bf s_{02}}$ в момент времени $t = 0:$

$ s_{0} = \sqrt {\displaystyle (s_{01} \cos \varphi _{1} + s_{02} \cos \varphi _{2} )^{2} + (s_{01} \sin \varphi _{1} + s_{02} \sin \varphi _{2} )^{2}}, $

$ \varphi _{0} = {\rm arctg\,}{\displaystyle \frac{\displaystyle {\displaystyle s_{01} \sin \varphi _{1} + s_{02} \sin \varphi _{2} }}{\displaystyle {\displaystyle s_{01} \cos \varphi _{1} + s_{02} \cos \varphi _{2} }}}. $

Ясно, что вертикальная проекция вектора ${\displaystyle \bf s_{0}}$ будет также изменяться по гармоническому закону с частотой $\omega _{0},$ поскольку взаимное расположение векторов $s_{01}$ и $s_{02}$ не изменяется с течением времени.

Рис. 1.6а.

Из этой диаграммы наглядно видно, что суммарное колебание $s(t)$ опережает по фазе колебание $s_{1} (t)$ и отстает по фазе от колебания $s_{2} (t).$ Полная фаза для каждого из трех колебаний в произвольный момент времени отличается от их начальных фаз на одну и ту же величину $\omega _{0} t,$ которую при построении векторных диаграмм не учитывают. При этом колебание изображается неподвижным вектором (рис. 1.6б), а частота колебания предполагается известной.

Рис. 1.6б.

Сложение взаимно-перпендикулярных колебаний.

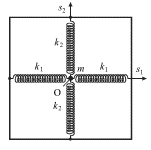
Рассмотрим колебательную систему, состоящую из точечного груза массы $m$ и четырех связанных с ним пружин (рис. 1.7) - усложненный вариант рассмотренного выше пружинного маятника.

Рис. 1.7.

Если масса движется по гладкой горизонтальной поверхности (на рисунке показан вид сверху), то ее мгновенное расположение описывается двумя смещениями из положения равновесия - точки О: $s_{1} (t)$ и $s_{2} (t).$ Такая система обладает двумя степенями свободы. Будем считать смещения малыми, чтобы, во-первых, выполнялся закон Гука, а, во-вторых, при смещении вдоль направления $s_{1}$ деформации пружин с жесткостью $k_{2}$ не приводили к сколько-нибудь заметному вкладу в возвращающую силу $F_{1} = - 2k_{1} s_{1} .$ Аналогично, при смещении в перпендикулярном направлении $s_{2}$ возвращающая сила $F_{2} = - 2k_{2} s_{2} .$ При таких условиях колебания в двух взаимно перпендикулярных направлениях происходят независимо друг от друга:

$ s_{1} (t) = s_{01} \sin (\omega _{01} t + \varphi _{1} ), \quad s_{2} (t) = s_{02} \sin (\omega _{02} t + \varphi _{2} ). $(1.19)

Здесь собственные частоты гармонических колебаний равны

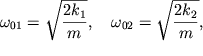$ \omega _{01} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2k_{1} }}{\displaystyle {\displaystyle m}}}}, \quad \omega _{02} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2k_{2} }}{\displaystyle {\displaystyle m}}}}, $(1.20)

а амплитуды и начальные фазы определяются начальными условиями.

При возбуждении колебаний в такой системе при произвольном соотношении собственных частот $\omega _{01}$ и $\omega _{02}$ траектория колеблющегося груза может быть чрезвычайно сложной. Ее, в принципе, можно проанализировать, принимая во внимание тот факт, что результирующее движение груза является суперпозицией двух взаимно-перпендикулярных независимых колебаний.

Рассмотрим вначале движение груза, если $\omega _{01} = \omega _{02} = \omega _{0}$ (жесткости всех пружин одинаковы). Чтобы получить траекторию движения, исключим из (1.19) текущее время. Для этого перепишем (1.19) в виде:

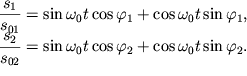$ \begin{array}{ l} {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}} = \sin \omega _{0} t\cos \varphi _{1} + \cos \omega _{0} t\sin \varphi _{1}, \\ {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}} = \sin \omega _{0} t\cos \varphi _{2} + \cos \omega _{0} t\sin \varphi _{2} . \\ \end{array} $(1.21)

Умножим первое уравнение (1.21) на $\cos \varphi _{2},$ а второе - на $\cos \varphi _{1}$ и вычтем второе уравнение из первого. В результате получим

$ {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}\cos \varphi _{2} - {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\cos \varphi _{1} = \cos \omega _{0} t\sin \left( {\displaystyle \varphi _{1} - \varphi _{2} } \right). $(1.22а)

Теперь умножим первое уравнение на $\sin \varphi _{2},$ а второе - на $\sin \varphi _{1},$ повторим вычитание и получим

$ {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}\sin \varphi _{2} - {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\sin \varphi _{1} = \sin \omega _{0} t\sin (\varphi _{2} - \varphi _{1} ). $(1.22б)

Наконец, возведем в квадрат каждое из равенств (1.22) и сложим их. В результате время будет исключено, а уравнение траектории движущегося груза будет уравнением эллипса:

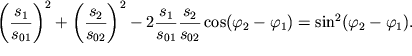$ \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} + \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}} \right)^{2} - 2{\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}{\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\cos (\varphi _{2} - \varphi _{1} ) = \sin ^{2}(\varphi _{2} - \varphi _{1} ). $(1.23)

Таким образом, в общем случае груз будет совершать периодические движения по эллиптической траектории. Направление движения вдоль траектории и ориентация эллипса относительно осей Os1 и Os2 зависят от начальной разности фаз $\Delta \varphi = \varphi _{2} - \varphi _{1} .$ На рис. 1.8 изображены траектории движения груза при различных значениях $\Delta \varphi .$

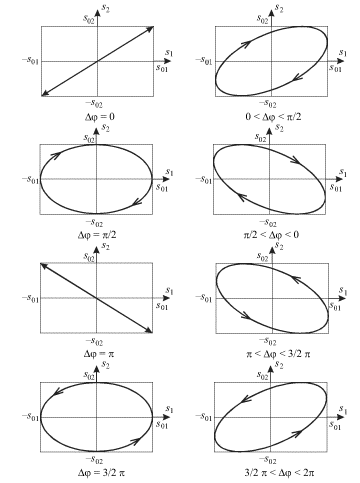Рис. 1.8.

Все траектории заключены в прямоугольник со сторонами $2s_{01}$ и $2s_{02}.$ При $\Delta \varphi = 0$ и $\Delta \varphi = \pi$ груз движется по прямой линии. При $\Delta \varphi = \pi / 2$ и $\Delta \varphi = 3\pi / 2$ полуоси эллипса совпадают с Os1 и Os2 (при $s_{10} = s_{20}$ эллипс вырождается в окружность). При разности фаз $0 \lt \Delta \varphi \lt \pi$ груз движется по часовой стрелке, а при $\pi \lt \Delta \varphi \lt 2\pi$ - против часовой стрелки.

Типичным примером двумерного осциллятора (маятника) является электрон в атоме, который движется вокруг ядра по эллиптической орбите с периодом обращения $T\sim 10^{ - 15} с.$ Можно считать, что такой электрон одновременно совершает два взаимно-перпендикулярных колебания с частотой $\omega _{0} = 2\pi / T\sim 10^{16}~с^{-1}.$

Если частоты двух взаимно-перпендикулярных колебаний не совпадают, но являются кратными: $m\omega _{02} = n\omega _{01},$ где $m$ и $n$ - целые числа, то траектории движения представляют собой замкнутые кривые, называемые фигурами Лиссажу (рис. 1.9). Отметим, что отношение частот колебаний равно отношению чисел точек касания фигуры Лиссажу к сторонам прямоугольника, в который она вписана.

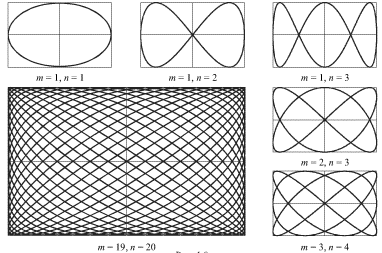Рис. 1.9.

Если кратность между частотами отсутствует, то траектории не являются замкнутыми и постепенно заполняют весь прямоугольник, напоминая нить в клубке.

Назад| Вперед

Rambler's Top100 Яндекс цитирования