Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page28.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Энергия, переносимая звуковой волной.

Интенсивность звука задается формулой (4.65)

$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho _{0} \omega ^{2}s_{0}^{2}$

(5.15)

и пропорциональна квадрату частоты. Поэтому при переходе в область высоких частот облегчается задача получения больших интенсивностей, необходимых, например, для наблюдения нелинейных эффектов (см. следующую лекцию). В зависимости от решаемой задачи в акустике используются волны с интенсивностью от 10^-8 Вт/см² до 10⁶ Вт/см².

Для практических целей интенсивность $I$ выражают через возмущение давления $\delta p,$ которое называют также "звуковым давлением". Наиболее просто такую зависимость можно получить из (5.15) при учете, что амплитуда скорости колебаний частиц $v_{0} = \omega s_{0}.$ С другой стороны, в соответствии с акустическим законом Ома (формула (3.53) в лекции по механике сплошных сред) эта скорость равна

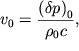$v_{0} = {\displaystyle \frac{\displaystyle {\displaystyle \left( {\displaystyle \delta p} \right)_{0} }}{\displaystyle {\displaystyle \rho _{0} c}}},$

(5.16)

где $\left( {\displaystyle \delta p} \right)_{0}$ - амплитуда колебаний возмущений давления $\delta p.$ Поэтому

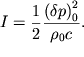$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle \left( {\displaystyle \delta p} \right)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}.$

(5.17)

Выполним некоторые простые оценки.

1. Вблизи струи газа, вытекающей из сопла реактивного двигателя самолета, амплитуда колебаний звукового давления $(\delta p)_{0} = 300 Па$ (вспомним, что $p_{0} = 10^{5} Па$ и $\left( {\displaystyle \delta p} \right)_{0} \ll p_{0}.$ Такое давление находится на пороге болевого ощущения (см. далее). Поскольку акустическое волновое сопротивление воздуха $z = \rho _{0} c = 41 см^{-2} \cdot с^{-1},$ то $v_{0} = 73 см/с.$ Если принять, что частота $\nu = 10^{3} Гц$ (хотя из турбины исходит многочастотный шум), то амплитуда смещения $s_{0} = v_{0} / 2\pi \nu = 0,01 см.$ Таким образом, смещение частиц воздуха даже при таком сильном звуке оказывается малым.

2. Звуки на пределе слышимости на частоте $\nu = 10^{3} Гц$ (ухо человека весьма чувствительно к этой частоте) имеют амплитуду звукового давления $(\delta p)_{0} = 2 \cdot 10^{ - 5} Па,$ а смещение частиц воздуха $s_{0} = 0,8 \cdot 10^{ - 9} см.$ Уместно заметить, что современные методы измерения смещений в принципе дают возможность зарегистрировать колебания с амплитудой $s_{0} \sim 10^{ - 16} см.$

3. В ультразвуковых волнах с частотами порядка нескольких мегагерц интенсивности могут достигать нескольких сотен Вт/см², а с использованием фокусирующих устройств - даже более десятка кВт/см². Это приводит к появлению огромных ускорений частиц среды, в которой распространяется ультразвуковая волна. Например, при распространении в воде волны с частотой $\nu = 10^{6} Гц$ и интенсивностью $I = 100 Вт/см^{2}$ амплитуда ускорения $a_{0} = \omega ^{2}s_{0},$ согласно (5.15), получается равной

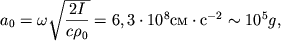$a_{0} = \omega \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2I}}{\displaystyle {\displaystyle c\rho _{0} }}}} = 6,3 \cdot 10^{8} см \cdot с^{-2} \sim 10^{5}g,$

(5.18)

что на пять порядков превосходит ускорение свободного падения $g.$ Учет появления таких громадных ускорений особенно важен в биологических исследованиях с применением ультразвука.

Поглощение звука.

Наличие вязкости и теплопроводности среды приводит к потере энергии звуковой волны, и эта энергия расходуется на нагревание среды. Волна давления $\delta p({\displaystyle \bf r},t),$ а также волны смещения $s({\displaystyle \bf r},t)$ и скорости $v({\displaystyle \bf r},t) = \partial s / \partial t$ по мере распространения затухают. Здесь $\bf r$ - радиус-вектор, задающий положение точки в трехмерном пространстве, в которой фиксируются возмущения давления, смещение частиц и их скорость. В случае гармонической волны, распространяющейся по одному направлению (вдоль оси Ox), возмущения давления записываются в виде

$\delta p(x,t) = (\delta p)_{0} e^{ - \alpha x}\sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle t - {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c}}}} \right)} \right]},$

(5.19)

где $\alpha$ - коэффициент затухания. Это уравнение характеризует плоскую волну (возмущение $\delta p$ в плоскости x = const одинаково). В этом случае отсутствует геометрическое расхождение волны. Амплитуда этой волны $(\delta p)_{0} e^{ - \alpha x}$ экспоненциально убывает с пройденным расстоянием. В соответствии с (5.17) интенсивность волны равна

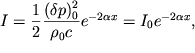$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}e^{ - 2\alpha x} = I_{0} e^{ - 2\alpha x},$

(5.20)

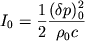где $I_{0} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}$ - начальная интенсивность волны. Если пренебречь потерями, связанными с теплопроводностью, то коэффициент $\alpha,$ согласно гидродинамике, оказывается равным

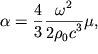$\alpha = {\displaystyle \frac{\displaystyle {\displaystyle 4}}{\displaystyle {\displaystyle 3}}}{\displaystyle \frac{\displaystyle {\displaystyle \omega ^{2}}}{\displaystyle {\displaystyle 2\rho _{0} c^{3}}}}\mu,$

(5.21)

где $\mu$ - вязкость жидкости или газа. Важно отметить, что $\alpha \sim \omega ^{2}.$ Этим объясняется тот факт, что резкий звук выстрела или щелчка кнута, в спектре которого присутствует широкий набор частот, по мере распространения трансформируется в более мягкий, поскольку в спектре остаются преимущественно низкие частоты. Заметим, что поглощение звука в воде существенно меньше, чем в воздухе, а в твердых телах еще меньше, чем в воде. Очень низким поглощением звука отличаются такие кристаллы, как сапфир, топаз, берилл, ниобат лития и другие.

В заключение отметим, что поглощение звука является главным препятствием, ограничивающим применение многих материалов на высоких частотах.

Излучатели звука.

Применяемые в акустике излучатели упругих волн можно подразделить на две большие группы.

К первой относятся излучатели-генераторы; колебания в них возбуждаются из-за наличия препятствия на пути постоянного потока газа или жидкости (сирены, свистки, генераторы Гартмана). Такие генераторы применяются в основном в диапазоне частот до $30\div 40 кГц.$ Они отличаются высоким коэффициентом преобразования кинетической энергии струи в акустическую (до 50%), простотой конструкции и эксплуатации, дешевизной. Интенсивность звука в непосредственной близости от излучателя может достигать 10 Вт/см². К недостаткам этих излучателей относятся широкий спектр излучаемых частот, нестабильность излучаемой мощности, невозможность получения звуковых колебаний заданной формы.

Вторую группу излучателей составляют электроакустические преобразователи. Свое название они получили оттого, что преобразуют электрические колебания в механические колебания какого-либо твердого тела, которое и излучает в окружающую среду акустические волны. Наиболее распространенные электроакустические преобразователи, такие, как электродинамические излучатели, магнитострикционные и пьезоэлектрические преобразователи, представляют собой линейные устройства, благодаря чему они возбуждают акустическую волну той же формы, что и электрический сигнал. Кроме того, эти устройства обратимы, то есть могут работать и как излучатели, и как приемники звука.

В диапазоне слышимых частот широкое распространение получили электродинамические излучатели, принцип действия которых основан на взаимодействии переменного электрического тока с магнитным полем (телефоны, громкоговорители). В магнитострикционных преобразователях используется эффект магнитострикции - деформации твердого тела в магнитном поле.

В ультразвуковом и гиперзвуковом диапазонах (до 10¹⁰ Гц) наиболее широко применяются пьезоэлектрические преобразователи, принцип действия которых основан на обратном пьезоэффекте - деформации тела под действием электрического поля.

На рис. 5.7 схематично показан простейший преобразователь, основу которого составляет пьезопластинка, вырезанная специальным образом из монокристалла кварца, ниобата лития (LiNbO₃) или другого пьезоматериала. К противоположным поверхностям пластинки (обычно металлизированным или покрытым металлическими электродами) прикладывается переменное напряжение $U$ с частотой $\nu.$ Толщина пластинки $\ell$ будет при этом периодически изменяться с той же частотой, причем это изменение не превосходит нескольких микрон. Вибрирующие поверхности пластинки приводят в движение соприкасающийся с ними воздух. Наибольшая амплитуда колебаний будет при резонансе, когда на толщине $\ell$ укладывается нечетное число полуволн:

$\ell = n{\displaystyle \frac{\displaystyle {\displaystyle \lambda _{n} }}{\displaystyle {\displaystyle 2}}}; n = 1, 3, 5 \ldots$

(5.22)

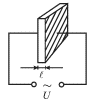Рис. 5.7.

Отметим, что при четном $n$ на электродах возникли бы электрические заряды одного знака, что невозможно. Резонансные частоты получаются равными

$\nu _{n} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda _{n} }}} = {\displaystyle \frac{\displaystyle {\displaystyle nc}}{\displaystyle {\displaystyle 2\ell }}}.$

(5.23)

Например, для пьезокварца при скорости продольных волн $c = 5700 м/с$ и толщине пластинки $\ell = 1 мм$ резонансные частоты равны

$\nu _{n} = n \cdot 2850 кГц.$

(5.24)

Наибольшую амплитуду колебаний имеет волна основной частоты $(n = 1),$ поэтому пьезоизлучатели применяются, как правило, на основной частоте.

На частотах до нескольких мегагерц широкое распространение получили преобразователи из пьезокерамики. Пьезокерамика представляет собой поликристаллический сегнетоэлектрический материал (твердые растворы на основе BaTiO₃-CaTiO₃, PbTiO₃-PbZnO₃ и другие), обладающий после поляризации в электрическом поле устойчивыми и сильными пьезоэлектрическими свойствами. Из пьезокерамики можно изготавливать излучатели самой разной формы (в виде пластин, стержней, колец и так далее). С помощью преобразователей сферической или цилиндрической формы получают сфокусированный ультразвуковой пучок, в фокусе которого интенсивность звука достигает $10^{5}\div 10^{6} Вт/см^{2}.$

На частотах порядка десятков и сотен мегагерц толщина $\ell$ становится настолько малой, что изготовить преобразователь можно лишь в жестком соединении со звукопроводом - массивным куском звукопроводящего материала. В этом случае на хорошо отполированную поверхность звукопровода напыляется металлическая пленка (один электрод), к которой приваривается толстая (порядка 1 мм) пластинка пьезоэлектрика. Затем эта пластинка сошлифовывается до нужной толщины $\ell,$ после чего на неё наносится второй электрод.

На частотах порядка 1 ГГц толщина пьезопреобразователя составляет $\ell \sim 1 мкм.$ Изготовление таких преобразователей представляет серьезную технологическую проблему. В этом частотном диапазоне применяются пленочные преобразователи, получаемые напылением на торец звукопровода пьезоэлектрических пленок из таких материалов, как CdS, ZnS, ZnO и другие. Современные технологии позволяют создавать преобразователи с коэффициентом преобразования электрической энергии в акустическую до 90% и мощностью волны, достигающей нескольких ватт.

Назад| Вперед