Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page24.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

В физике используют понятие плотности потока энергии, определяемой количеством энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Согласно (4.57), эта плотность равна

$J = {\displaystyle \frac{\displaystyle {\displaystyle \Delta W}}{\displaystyle {\displaystyle \Delta t}}} = wc$

(4.58)

и имеет размерность [J] = Дж/(м²*с).

Если площадка имеет площадь $dS,$ а ее нормаль $\bf n$ составляет с направлением распространения волны (осью Oх) угол $\alpha$ (рис. 4.20), то количество энергии, переносимое волной через эту площадку за единицу времени (поток энергии) равен

$d\Phi = wc \cdot dS\cos \alpha.$

(4.59)

Рис. 4.20.

Профессором МГУ Н.А. Умовым в 1874 г. был введен вектор плотности потока энергии

${\displaystyle \bf J} = wc,$

(4.60)

получивший название вектора Умова. С его использованием поток $d\Phi$ может быть записан в виде

$d\Phi = {\displaystyle \bf J} \cdot d{\displaystyle \bf S} = JdS\cos \alpha,$

(4.61)

где $d{\displaystyle \bf S} = dS \cdot {\displaystyle \bf n}.$

С подобным представлением потока вектора скорости мы встречались при изучении движения жидкостей.

Удобство вектора Умова становится особенно ощутимым, когда волна распространяется в трехмерном пространстве. Тогда поток энергии через произвольную поверхность $S$ выражается в виде интеграла по этой поверхности:

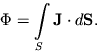$\Phi = {\displaystyle \int\limits_{S} {\displaystyle {\displaystyle \bf J} \cdot d{\displaystyle \bf S}} }.$

(4.62)

Последняя формула будет использована ниже.

Подсчитаем среднее значение за период вектора Умова для бегущей вдоль стержня поперечной гармонической волны

$s(x,t) = s_{0} \sin (\omega t - kx).$

(4.63)

Объемная плотность энергии (сумма потенциальной и кинетической энергий) равна

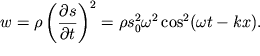$w = \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2} = \rho s_{0}^{2} \omega ^{2}\cos ^{2}(\omega t - kx).$

(4.64)

В некоторый момент времени она распределена вдоль стержня так, как показано на рис. 4.21. С течением времени это распределение смещается вдоль оси Oх со скоростью $с.$ Плотность потока энергии через любое сечение x = const будет периодически возрастать от нуля до максимальной величины $\rho s_{0}^{2} \omega ^{2}.$ Поэтому удобно пользоваться средним значением $J$ за период $T = 2\pi / \omega.$ Эта величина называется интенсивностью бегущей волны и равна

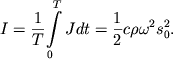$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle T}}}{\displaystyle \int\limits_{0}^{T} {\displaystyle Jdt = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho \omega ^{2}s_{0}^{2}.} }$

(4.65)

Важно отметить, что интенсивность пропорциональна квадрату амплитуды.

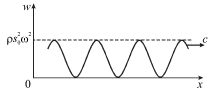Рис. 4.21.

В стоячей волне нет переноса энергии, т. к. она является суперпозицией двух бегущих волн, переносящих одинаковое количество энергии в противоположных направлениях. Однако, локальное движение энергии в ограниченном пространстве между соседними узлами все же происходит. В самом деле, запишем уравнение стоячей волны (4.34), опустив в нем постоянные фазовые добавки $\varphi _{отр} / 2 и k\ell$ :

$s(x,t) = 2s_{0} \cos kx\sin \omega t.$

(4.66)

Объемная плотность энергии деформации сдвига равна:

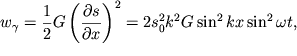$w_{\gamma } = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} = 2s_{0}^{2} k^{2}G\sin ^{2}kx\sin ^{2}\omega t,$

(4.67)

а объемная плотность кинетической энергии выражается как:

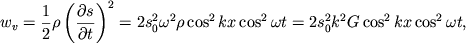$w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2} = 2s_{0}^{2} \omega ^{2}\rho \cos ^{2}kx\cos ^{2}\omega t = 2s_{0}^{2} k^{2}G\cos ^{2}kx\cos ^{2}\omega t,$

(4.68)

поскольку 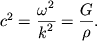$c^{2} = {\displaystyle \frac{\displaystyle {\displaystyle \omega ^{2}}}{\displaystyle {\displaystyle k^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}.$

Локальное движение энергии наглядно демонстрирует рис. 4.22, на котором показан фрагмент стоячей волны в моменты времени $t_{1} = 0$ и $t_{2} = t_{1} + T / 4$ (а) и соответствующие распределения $w_{\gamma }$ (б) и $w_{v}$ (в).

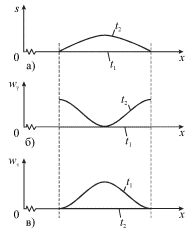Рис. 4.22.

Видно, что при $t = t_{1},$ когда элементы стержня проходят положение равновесия и имеют максимальные скорости, деформация отсутствует $(w_{\gamma } = 0),$ а вся энергия запасена в виде кинетической энергии $w_{v}$ и локализована вблизи пучности. Однако через четверть периода колебаний частицы стержня сместятся на максимальные расстояния и остановятся $(w_{v} = 0).$ Энергия будет запасена в виде потенциальной энергии $w_{\gamma }$ и локализована вблизи узлов. Это означает, что энергия из области вблизи пучности за четверть периода колебаний перетекает в обе стороны по направлению к узлам. Затем она движется в обратном направлении, и этот процесс повторяется многократно. Поток энергии через узлы отсутствует. Среднее за период значение потока энергии через любое сечение x = const будет равно нулю $(I = 0).$

Продольные волны.

Такие волны могут быть возбуждены ударом молотка по одному из торцов упругого стержня. Возмущение, распространяющееся вдоль стержня, визуально незаметно, однако основные закономерности такого волнового процесса можно смоделировать, если вместо стержня использовать длинную пружину с большим диаметром витков (рис. 4.23). Если эту пружину подвесить горизонтально на нескольких нитях (не показанных на рисунке) и резко ударить ладонью по левому торцу, то по ней побежит импульс сжатия с некоторой скоростью $c.$ На рис. 4.23а этот импульс имеет длину $c\tau _{и}$ ( $\tau _{и}$ - длительность импульса, равная длительности удара). Добежав до правого конца пружины, он отразится, при этом, если конец закреплен (рис. 4.23б), то отраженный импульс будет также импульсом сжатия. Если правый конец свободен, то отраженный импульс будет импульсом растяжения (рис. 4.23в). Он возникает в момент смещения вправо свободного конца пружины, когда до него добежит импульс сжатия. Эта ситуация напоминает смещение свободного конца шнкрв. Отметим, что в рассмотренном случае смещения витков пружины происходят вдоль направления распространения волны, поэтому волна называется продольной.

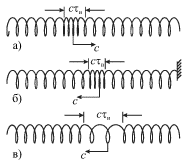Рис. 4.23.

Рассмотрим теперь распространение импульсов сжатия и растяжения в стержне.

Мысленно разобьем стержень на ряд элементов длиной $dx$ каждый. При распространении продольной волны концы каждого элемента, отмеченные на рис. 4.24 сплошными линиями, будут смещены в новые положения, отмеченные пунктиром. Эти смещения s будем считать положительными, если они происходят в положительном направлении оси Oх, и отрицательными - в противоположном случае.

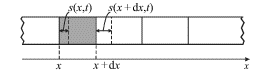Рис. 4.24.

Пусть левый конец некоторого элемента, имеющий координату х, сместился в данный момент времени $t$ на расстояние $s(x,t),$ а правый конец - на $s(x + dx,t).$ Деформация растяжения (сжатия) определяется относительным удлинением элемента $dx$ :

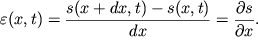$\varepsilon (x,t) = {\displaystyle \frac{\displaystyle {\displaystyle s(x + dx,t) - s(x,t)}}{\displaystyle {\displaystyle dx}}} = {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

(4.69)

Отметим, деформации растяжения соответствует $\varepsilon \gt 0,$ а сжатия - $\varepsilon \lt 0.$

В отличие от поперечной волны, при растяжении (сжатии) уменьшается (увеличивается) плотность среды $\rho.$ Ее можно представить в виде

$\rho = \rho _{0} + \delta \rho ; \vert \delta \rho \vert \ll \rho _{0}.$

(4.70)

Здесь $\delta \rho$ - малая добавка к равновесной плотности $\rho _{0},$ причем $\delta \rho$ может быть как положительной, так и отрицательной. С учетом постоянства массы деформируемого элемента $dx$ можем записать

$\rho _{0} dx = (\rho _{0} + \delta \rho )[dx + s(x + dx,t) - s(x,t)] = (\rho _{0} + \delta \rho )dx(1 + \varepsilon ).$

(4.71)

Раскрывая скобки и пренебрегая малой величиной $\varepsilon \cdot \delta \rho,$ находим

${\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} = - \varepsilon.$

(4.72)

Спустя некоторое время $t$ после удара по торцу стержня (или после резкого оттягивания этого торца) распределение смещений $s,$ деформаций $\varepsilon$ и возмущений плотности $\delta \rho$ в бегущих импульсах сжатия и растяжения будут иметь вид, показанный на рис. 4.25. Пунктиром показаны распределения всех величин в один из последующих моментов времени.

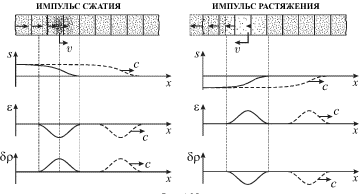Рис. 4.25.

Уравнение волны, бегущей вдоль оси Oх, в обоих случаях имеет вид $s(x,t) = s(t - x / c).$ По аналогии с (4.54) деформация $\varepsilon = \partial s / \partial x$ и колебательная скорость $v = \partial s / \partial t$ элемента связаны соотношением

${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}, \; или \; \varepsilon = - {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.73)

Подчеркнем, что в импульсе сжатия $(\varepsilon \lt 0)$ скорость $v$ совпадает по направлению со скоростью $с,$ а в импульсе растяжения они имеют противоположные направления.

Рассчитаем скорость распространения продольных волн. На рис. 4.26 изображен фрагмент стержня и показан его элемент $dx,$ к концам которого приложены нормальные напряжения $\sigma _{n}.$ Уравнение движения элемента с поперечным сечением равным $S$ имеет вид:

$dm{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = S{\displaystyle \left[ {\displaystyle \sigma _{n} (x + dx,t) - \sigma _{n} (x,t)} \right]},$

(4.74)

где $dm = \rho _{0} Sdx.$ Чтобы (4.74) преобразовать к волновому уравнению, необходимо связать напряжения $\sigma _{n}$ с деформациями элементов стержня. Наиболее просто это можно сделать для тонкого стержня.

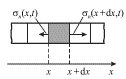Рис. 4.26.

Скорость волн в тонком стержне.

Если стержень тонкий, то деформации и напряжения вдоль координаты х связаны известным законом Гука:

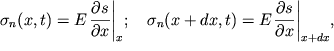$\sigma _{n} (x,t) = E{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x} ; \quad \sigma _{n} (x + dx,t) = E{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx},$

(4.75)

где $Е$ - модуль Юнга.

Подставляя (4.75) в (4.74) и производя деление на $\rho _{0} Sdx,$ получаем волновое уравнение:

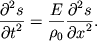${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}}.$

(4.76)

Скорость продольных волн получается равной

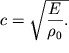$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}.}$

(4.77)

Эта скорость превышает скорость поперечных волн (см. формулу (4.49)), поскольку $E \gt G.$ По порядку величины обе скорости совпадают и для различных материалов преимущественно лежат в диапазоне $c\sim (10^{3}\div 10^{4}) м/c.$

Назад| Вперед