Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page14.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Свободные незатухающие колебания в системах с двумя степенями свободы. Нормальные колебания (моды). Парциальные и нормальные частоты. Биения. Понятие спектра колебаний. Методика анализа колебаний 2-х связанных осцилляторов. Затухание колебаний и диссипация энергии. Вынужденные колебания. Резонанс. Колебания систем со многими степенями свободы. Дисперсионное соотношение.

Наблюдая колебания массы $m,$ подвешенной на легкой пружине жесткости $k_{1},$ нельзя не обратить внимание на то, что, наряду с вертикальными колебаниями груза, возникают и так называемые маятниковые колебания (из стороны в сторону) (рис. 3.1).

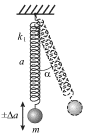Рис. 3.1.

Наиболее сильными эти маятниковые колебания будут тогда, когда частота вертикальных колебаний $\sqrt {\displaystyle k_{1} / m}$ будет равна удвоенной частоте маятниковых колебаний $\sqrt {\displaystyle g / a}$ ( $а$ - длина растянутой пружины при неподвижном грузе). Такой результат легко понять, если рассматривать маятниковые колебания как резонансные параметрические колебания, при этом параметр маятника - длина пружины $а$ - меняется при вертикальных колебаниях на величину $\pm \Delta a$ (см. предыдущую лекцию). В течение некоторого времени маятниковые колебания могут усиливаться за счет уменьшения энергии вертикальных колебаний. Затем процесс пойдет в обратном направлении: маятниковые колебания начнут ослабевать, "возвращая" энергию усиливающимся вертикальным колебаниям. Следовательно, вертикальные колебания не будут гармоническими, что связано с наличием маятниковых колебаний, соответствующих возбуждению второй степени свободы. При определенных условиях могут возникать и крутильные колебания груза вокруг вертикальной оси пружины. Опыт показывает, что наиболее сильными эти колебания будут в том случае, когда их частота $\sqrt {\displaystyle k_{2} / J} (k_{2}$ - коэффициент жесткости пружины при ее скручивании, рассмотренный в лекции по деформации твердого тела, $J$ - момент инерции тела относительно вертикальной оси) будет примерно в два раза меньше частоты вертикальных колебаний. В общем случае в этой системе могут происходить четыре типа колебаний, соответствующих четырем степеням свободы: одно вертикальное, два маятниковых в двух взаимно-перпендикулярных плоскостях и одно крутильное.

Таким образом, перед нами возникает задача изучения основных закономерностей колебаний в системах с двумя, тремя и более степенями свободы, затем можно рассмотреть и колебания сплошной среды, как системы с бесконечно большим числом степеней свободы.

Свободные незатухающие колебания в системах с двумя степенями свободы.

На рис. 3.2 изображены три различные колебательные системы с двумя степенями свободы. Первая из них (а) - это два различных пружинных маятника, связанные пружиной с жесткостью ${\displaystyle k}'.$ Вторая (б) - два груза с массами $m_{1}$ и $m_{2} ,$ закрепленные на натянутом некоторой силой $F$ невесомом резиновом шнуре. Третья (в) - два связанных пружиной ${\displaystyle k}'$ различных маятника, каждый из которых состоит из груза, подвешенного на невесомом стержне.

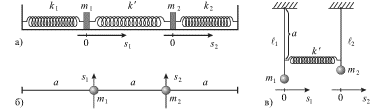Рис. 3.2.

Колебания грузов в каждой из трех систем описываются двумя временными зависимостями их смещений $s_{1} (t)$ и $s_{2} (t).$ Положительное направление смещения $s$ на рисунке указано стрелками.

Опыт показывает, что при произвольном способе возбуждения колебания не будут гармоническими: амплитуда колебаний каждой из масс будет периодически меняться во времени. Однако можно создать такие начальные условия, при которых каждый груз будет совершать гармонические колебания с одной и той же частотой $\omega$ :

(3.1)

$\begin{array}{l} s_{1} (t) = s_{01} \sin (\omega t + \varphi ); \\ s_{2} (t) = s_{02} \sin (\omega t + \varphi ). \\ \end{array}$

Частота этих колебаний \omega определяется свойствами системы. Отношение

(3.2)

$\varsigma = s_{02} / s_{01}$

также определяется параметрами системы. Эта безразмерная алгебраическая величина $\varsigma$ называется коэффициентом распределения амплитуд при гармоническом колебании. Отметим, что $s_{01}$ и $s_{02}$ могут иметь любой знак. Если $\varsigma \gt 0,$ то смещения обеих масс всегда происходит в одну сторону (синфазные колебания), а при $\varsigma \lt 0$ - в противоположные стороны (противофазные колебания). Гармонические колебания (3.1) называются нормальными колебаниями, или модами, а частота $\omega$ называется нормальной частотой. Таким образом, мода характеризуется двумя параметрами: частотой $\omega$ и коэффициентом $\varsigma ,$ определяющим "конфигурацию" моды.

Практика показывает, что в системе с двумя степенями свободы могут существовать синфазные гармонические колебания с частотой $\omega _{I}$ и противофазные гармонические колебания с частотой $\omega _{II} \gt \omega _{I} .$

Следовательно, в системе могут быть возбуждены две моды:

I мода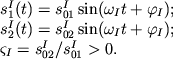

$\begin{array}{l} s_{1}^{I} (t) = s_{01}^{I} \sin (\omega _{I} t + \varphi _{I} ); \\ s_{2}^{I} (t) = s_{02}^{I} \sin (\omega _{I} t + \varphi _{I} ); \\ \varsigma _{I} = s_{02}^{I} / s_{01}^{I} \gt 0. \\ \end{array}$

(3.3)

II мода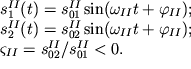

$\begin{array}{l} s_{1}^{II} (t) = s_{01}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ s_{2}^{II} (t) = s_{02}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ \varsigma _{II} = s_{02}^{II} / s_{01}^{II} \lt 0. \\ \end{array}$

(3.4)

Нетрудно теперь понять, что любое колебание связанной линейной системы с двумя степенями свободы (а именно такие системы мы будем далее рассматривать) может быть представлено в виде суперпозиции двух нормальных колебаний (3.3) и (3.4):

(3.5)

$\begin{array}{l} s_{1} (t) = s_{1}^{I} (t) + s_{1}^{II} (t) = s_{01}^{I} \sin (\omega _{I} t + \varphi _{I} ) + s_{01}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ s_{2} (t) = s_{2}^{I} (t) + s_{2}^{II} (t) = s_{02}^{I} \sin (\omega _{I} t + \varphi _{I} ) + s_{02}^{II} \sin (\omega _{II} t + \varphi _{II} ). \\ \end{array}$

Не прибегая пока к детальному математическому исследованию, проанализируем поведение системы с двумя степенями свободы, пользуясь основными идеями, развитыми в предыдущих лекциях. Представим любую из систем, изображенных на рис. 3.2, как сложную систему, состоящую из двух парциальных систем. Эти парциальные системы, соответствующие случаю (а) рис. 3.2, показаны на рис. 3.3: каждая из этих парциальных систем имеет собственную частоту колебаний, которая называется парциальной частотой.

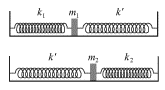Рис. 3.3.

Величины этих парциальных частот, соответственно, равны:

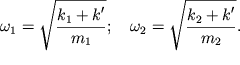(3.6)

$\omega _{1} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{1} + {\displaystyle k}'}}{\displaystyle {\displaystyle m_{1} }}}} ; \quad \omega _{2} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{2} + {\displaystyle k}'}}{\displaystyle {\displaystyle m_{2} }}}} .$

Совершенно очевидно, что частота $\omega _{1}$ - это частота колебаний массы $m_{1}$ в системе двух связанных маятников, когда масса $m_{2}$ неподвижна (заблокирована вторая степень свободы). Аналогично, с частотой $\omega _{2}$ будет колебаться масса $m_{2} ,$ когда неподвижна масса $m_{1} .$

Теперь перейдем к определению нормальных частот $\omega _{I}$ и $\omega _{II} .$ Вспомним, что квадрат частоты гармонических колебаний равен отношению возвращающей силы к смещению груза $s$ и величине его массы $m.$ Подберем начальные смещения масс $m_{1}$ и $m_{2}$ таким образом, чтобы для обеих масс эти отношения (а, следовательно, и частоты) были бы одинаковы. Такой подбор легко угадывается для симметричной системы $(m_{1} = m_{2} = m, k_{1} = k_{2} = k),$ (рис. 3.4), у которой парциальные частоты совпадают:

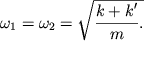(3.7)

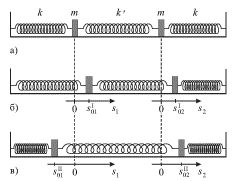$\omega _{1} = \omega _{2} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + {\displaystyle k}'}}{\displaystyle {\displaystyle m}}}.}$

Рис. 3.4

Если оба груза сместить вправо на одинаковые расстояния $s_{01}^{I} = s_{02}^{I} ,$ то средняя пружина ${\displaystyle k}'$ (пружина связи) не будет деформирована (позиция б). После отпускания пружина будет оставаться недеформированной. Поэтому каждый из грузов будет совершать гармонические колебания с одной и той же частотой

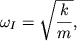(3.8)

$\omega _{I} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle m}}}} ,$

которая и является первой нормальной частотой. Конфигурация этого синфазного колебания (моды) задается коэффициентом распределения амплитуд $\varsigma _{I} = + 1.$

Если теперь обе массы сместить в разные стороны на одинаковые расстояния $s_{02}^{II} = - s_{01}^{II}$ (позиция в), то пружина ${\displaystyle k}'$ удлинится на величину $2s_{02}^{II} .$ Поэтому к правой массе будет приложена возвращающая сила, равная $- (ks_{02}^{II} + 2{\displaystyle k}'s_{02}^{II} ),$ а на левую массу будет действовать в противоположном направлении сила $- (ks_{01}^{II} + 2{\displaystyle k}'s_{01}^{II} ).$ После отпускания грузы будут совершать противофазные гармонические колебания со второй нормальной частотой

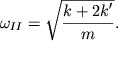(3.9)

$\omega _{II} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + 2{\displaystyle k}'}}{\displaystyle {\displaystyle m}}}} .$

Конфигурация второй моды характеризуется коэффициентом распределения $\varsigma _{II} = - 1.$

Назад| Вперед

Колебания и волны. Лекции.

Лекция 3

Свободные незатухающие колебания в системах с двумя степенями свободы.