Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page13.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Маятник на вращающемся валу (маятник Фруда).

Для более углубленного изучения принципа действия автоколебательной системы проанализируем колебания маятника, подвес которого скреплен с муфтой 1, одетой на горизонтальный вал 2 (рис. 2.10).

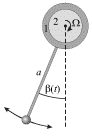Рис. 2.10.

Пусть вал вращается с постоянной угловой скоростью $\Omega$ по часовой стрелке. Если угол отклонения маятника от вертикали $\beta (t)$ меняется с течением времени, то сила сухого трения в подвесе, нелинейно зависящая от относительной скорости муфты и вала $\Omega - \dot {\displaystyle \beta },$ также будет меняться во времени ( $\dot {\displaystyle \beta }$ - угловая скорость муфты). Момент этой силы $М_{тр}$ будет оказывать периодическое воздействие на маятник, поддерживая его колебания. На рис. 2.11 изображена нелинейная зависимость $М_{тр}$ от относительной угловой скорости муфты и вала. На изображенной кривой имеется точка перегиба P. Подберем скорость вращения вала $\Omega$ такой, чтобы в отсутствие колебаний $(\dot {\displaystyle \beta } = 0)$ попасть в эту точку. В этом случае к муфте маятника будет приложен постоянный момент силы трения: $M_{тр} = M_{0} .$ Для дальнейшего анализа более удобно воспользоваться зависимостью $M_{тр} (\dot {\displaystyle \beta }),$ изображенной на рис. 2.12. Следует подчеркнуть, что начальное (линейное) нарастание $М_{тр}$ с угловой скоростью $\dot {\displaystyle \beta }$ обеспечивает условие для самопроизвольного нарастания колебаний из флуктуации, что эквивалентно наличию положительной обратной связи, а последующее замедление роста $М_{тр}$ при увеличении $\dot {\displaystyle \beta }$ является причиной нелинейного ограничения нарастания колебаний: амплитуда смещения маятника (а значит и амплитуда его скорости $\dot {\displaystyle \beta }_{\max } )$ достигнет максимальной (установившейся) величины, что эквивалентно наличию нелинейного ограничителя.


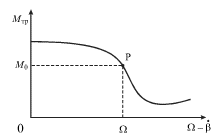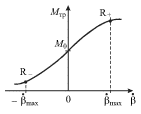Рис. 2.11.	Рис. 2.12.

Отклоним осторожно маятник от вертикали на угол $\beta _{0}$ такой, чтобы момент силы трения, действующий на неподвижный маятник, $M _{0} = M_{тр} (0),$ был уравновешен моментом силы тяжести $M(\beta _{0} ) = mga\sin \beta _{0}$ :

$M_{тр} (0) = M(\beta _{0} ),или \quad M_{0} = mga\sin \beta _{0} .$

(2.63)

Здесь $m$ - масса маятника, $a$ - расстояние от вала до центра масс маятника.

На первый взгляд, может показаться, что маятник так и останется висеть под углом $\beta _{0}$ к вертикали. На самом деле это положение будет неустойчивым. Представим, что в результате ничтожного толчка маятник приобретет небольшую угловую скорость $\dot {\displaystyle \beta } \gt 0.$ При этом возрастут моменты сил тяжести $М$ и трения $М_{тр},$ и условие (2.63) может нарушиться. Если начальный наклон кривой $М_{тр}(\dot {\displaystyle \beta })$ на рис. 2.12 достаточно велик (сильная положительная обратная связь), то $M_{тр} (\dot {\displaystyle \beta }) \gt M(\beta _{0} ).$ Это означает, что угловая скорость $\dot {\displaystyle \beta }$ будет нарастать. Однако затем это нарастание прекратится, т.к. из-за нелинейного загиба кривой $М_{тр}(\dot {\displaystyle \beta })$ равенство моментов опять восстановится (сработает механизм нелинейного ограничения):

$M_{тр} (\dot {\displaystyle \beta }_{\max } ) = M(\beta ).$

(2.64)

Условию (2.64) соответствует точка $R_{ + }$ на кривой $М_{тр}(\dot {\displaystyle \beta }).$ После этого угловая скорость начнет уменьшаться, поскольку с ростом угла $\beta$ момент $M(\beta )$ продолжает расти, а $М_{тр}(\dot {\displaystyle \beta })$ - убывать. Следовательно, маятник спустя какое-то время остановится, а его угол отклонения достигнет максимальной величины $\beta _{\max } .$ Поскольку в этот момент $M(\beta _{\max } ) \gt M_{тр} = M_{0} ,$ то маятник начнет двигаться в обратном направлении. Момент силы тяжести начнет уменьшаться, а момент силы трения будет также уменьшаться, но быстрее, чем момент силы тяжести (опять срабатывает положительная обратная связь). Сначала это движение будет ускоренным, пока $M \gt M_{тр}$ (до точки R_- на рис. 2.12), а затем при $M \lt M_{тр}$ - замедленным (до точки P на рис. 2.12). Остановившись при некотором угле наклона $\beta _{\min } ,$ маятник опять движется влево, т.к. все еще $M \lt M_{тр} .$ Наконец, он достигает стартовой позиции, однако приобретенная им скорость будет больше скорости начального толчка. Таким образом, в течение одного периода колебаний увеличилась энергия маятника за счет ее заимствования от устройства, вращающего вал.

В последующие периоды колебаний точки R₊ и R $-$ на кривой $M_{тр} (\dot {\displaystyle \beta })$ будут сдвигаться в разные стороны, однако из-за нелинейности кривой этот сдвиг прекратится (срабатывает механизм нелинейного ограничения), и колебания установятся.

Чтобы количественно проанализировать автоколебания маятника, запишем уравнение вращательного движения маятника с моментом инерции $J$ :

$J\ddot {\displaystyle \beta } = M_{тр} (\dot {\displaystyle \beta }) - mga\sin \beta .$

(2.65)

В этом уравнении мы пока пренебрежем моментом силы вязкого трения, действующей на движущийся маятник. Момент силы сухого трения в подвесе, нелинейно зависящий от угловой скорости $\dot {\displaystyle \beta }$ (см. рис. 2.12), можно аппроксимировать следующим выражением

$M_{тр} (\dot {\displaystyle \beta }) = M_{0} + k_{1} \dot {\displaystyle \beta } - k_{2} \dot {\displaystyle \beta }^{3},$

(2.66)

где $k_{1}$ и $k_{2}$ - размерные коэффициенты, определяющие обратную связь и нелинейное ограничение соответственно. Если колебание описывать углом отклонения $\alpha$ от положения неустойчивого равновесия, задаваемого углом $\beta _{0} (\alpha = \beta - \beta _{0} ),$ то

$mga\sin \beta = mga(\sin \beta _{0} \cos \alpha + \cos \beta _{0} \sin \alpha ).$

(2.67)

Для малых углов $\alpha \cos \alpha \approx 1, \sin \alpha \approx \alpha .$ Если учесть далее, что $\dot {\displaystyle \beta } = \dot {\displaystyle \alpha },$ то уравнение (2.65) примет вид:

$J\ddot {\displaystyle \alpha } + mga\cos \beta _{0} \alpha = k_{1} \dot {\displaystyle \alpha } - k_{2} \dot {\displaystyle \alpha }^{3}.$

(2.68)

Это уравнение является нелинейным дифференциальным уравнением и не имеет аналитического решения. В теории колебаний развиты методы, позволяющие решить его приближенно, исследовать условия, при которых возможно самовозбуждение колебаний, и найти амплитуду $\alpha _{0}$ и частоту $\omega$ установившихся колебаний:

$\alpha (t) = \alpha _{0} \sin \omega t.$

(2.69)

Мы же поступим более просто и определим $\alpha _{0}$ из условия энергетического баланса. Поскольку правая часть (2.68) мала, то частота колебаний приближенно равна: $\omega = \sqrt {\displaystyle {\displaystyle {\displaystyle mga\cos \beta _{0} } / {\displaystyle J}}} .$

Подсчитаем работу за период колебаний $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega ,}}$ совершаемую устройством (например, электродвигателем), вращающим вал. Она, очевидно, равна:

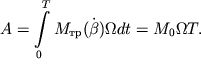$A = {\displaystyle \int\limits_{0}^{T} {\displaystyle M_{тр} (\dot {\displaystyle \beta })\Omega dt = M_{0} \Omega T.} }$

(2.70)

Здесь учтено, что интегралы по времени от $\dot {\displaystyle \beta }$ и $\dot {\displaystyle \beta }^{3}$ равны нулю, поскольку

$\dot {\displaystyle \beta } = \dot {\displaystyle \alpha } = \alpha _{0} \omega \cos \omega t.$

(2.71)

Потери энергии в скользящем подвесе за это время составят величину

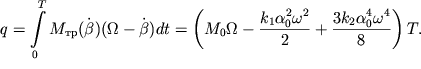$q = {\displaystyle \int\limits_{0}^{T} {\displaystyle M_{тр} (\dot {\displaystyle \beta })(\Omega - \dot {\displaystyle \beta })dt} } = \left( {\displaystyle M_{0} \Omega - {\displaystyle \frac{\displaystyle {\displaystyle k_{1} \alpha _{0}^{2} \omega ^{2}}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle 3k_{2} \alpha _{0}^{4} \omega ^{4}}}{\displaystyle {\displaystyle 8}}}} \right)T.$

(2.72)

На рис. 2.13 изображены зависимости $A$ и $q$ от амплитуды $\alpha _{0} .$ Видно, что при случайных флуктуациях, когда $\alpha _{0}$ мало, $A \gt q.$ Это означает, что колебания будут нарастать. Однако с ростом амплитуды начинают расти потери $q$ . Колебания установятся при $A = q$ (точка R на графике). Амплитуда установившихся колебаний определится из равенства

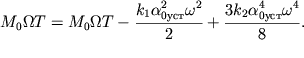$M_{0} \Omega T = M_{0} \Omega T - {\displaystyle \frac{\displaystyle {\displaystyle k_{1} \alpha _{0уст}^{2} \omega ^{2}}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle 3k_{2} \alpha _{0уст}^{4} \omega ^{4}}}{\displaystyle {\displaystyle 8}}}.$

(2.73)

Отсюда

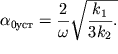$\alpha _{0уст} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle \omega }}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{1} }}{\displaystyle {\displaystyle 3k_{2} }}}.}$

(2.74)

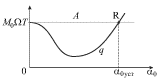Рис. 2.13.

Заметим, что теперь мы можем легко учесть силы вязкого трения, для чего в правую часть уравнения (2.68) следует добавить член - $\Gamma \dot {\displaystyle \alpha }.$ Это приведет к тому, что $k_{1}$ в (2.74) будет уменьшен на величину $\Gamma .$ Поэтому (2.74) изменится:

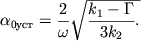(2.)

Из последнего выражения следует, что при $\Gamma \ge k_{1}$ колебания не могут самопроизвольно начаться.

Автоколебательные системы находят широчайшее применение в технике. Так, например, духовые и смычковые инструменты, органные трубы, генераторы электромагнитного излучения в приемно-передающих линиях связи, оптические квантовые генераторы (лазеры) и др. представляют примеры автоколебательных систем.

Однако, автоколебания могут играть и негативную роль, начиная от безобидных колебаний деталей кранов водопроводных систем, "ревущих" при достаточном напоре воды, до опасных колебаний крыльев самолетов, получивших название "флаттер". В ноябре 1940 г. подвесной мост через реку Такома в США разрушился из-за крутильных автоколебаний, возникших под действием дувшего вдоль реки ветра.

Назад| Вперед