Астронет > Механика твердого тела. Лекции.

Астронет: Физический факультет МГУ Механика твердого тела. Лекции.
http://variable-stars.ru/db/msg/1175788/page4.html

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Движение твердого тела с одной неподвижной точкой.

Примеры таких тел показаны на рис. 1.20: волчок с шарнирно закрепленным острием (а), конус, катающийся по плоскости без проскальзывания (б). В этом случае тело имеет три степени свободы - начала систем XYZ и x₀y₀z₀, введенных в начале лекции, можно совместить с точкой закрепления, а для описания движения тела использовать три угла Эйлера:

$\varphi = \varphi (t); \psi = \psi (t); \theta = \theta (t).$

(1.22)

Для твердого уела с одной неподвижной точкой справедлива теорема Эйлера: твердое тело, закрепленное в одной точке, может быть переведено из одного положения в любое другое одним поворотом на некоторый угол вокруг неподвижной оси, проходящей через точку закрепления. Доказательство этой теоремы можно найти в учебниках. Для нас важно следствие из этой теоремы: движение закрепленного в точке твердого тела в каждый момент времени можно рассматривать как вращение вокруг мгновенной оси, проходящей через точку закрепления. Естественно, что положение этой оси как в пространстве, так и относительно самого тела с течением времени в общем случае меняется.

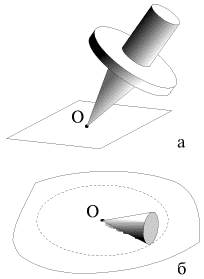Рис. 1.20.

Геометрическое место положений мгновенной оси вращения относительно неподвижное системы XYZ (или x₀y₀z₀) - это сложная коническая поверхность с вершиной в точке закрепления. В теоретической механике ее называют неподвижным аксоидом. Геометрическое место положений мгновенной оси вращения относительно подвяжись системы xyz, жестко связанной с твердым телом, - это тоже коническая поверхность - подвижный аксоид. Например, в случае конуса AO₁, катящегося по поверхности другого конуса AO₂ без проскальзывания (рис. 1.21; точка А подвижного конуса шарнирно закреплена) неподвижный аксоид совпадает с поверхностью неподвижного конуса AO₂, а подвижный аксоид - с поверхностью подвижного конуса AO₁.

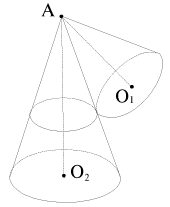Рис. 1.21.

Скорость произвольной точки твердого тела можно рассчитать как линейную скорость вращательного движения вокруг мгновенной оси:

${\displaystyle \bf v} = \omega\times {\displaystyle \bf r},$

(1.23)

где r - радиус-вектор точки относительно начала системы XYZ или x₀y₀z₀, совмещенного с точкой закрепления. Следует только иметь в виду, что, в отличие от вращения вокруг неподвижной оси, "плечо" вектора v (расстояние рассматриваемой точки до мгновенной оси вращения) является функцией времени.

Ускорение произвольной точки твердого тела

$\bf a} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle \bf r} + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}}}{\displaystyle {\displaystyle dt}}$

(1.24)

состоит из двух частей: ускорения, связанного с неравномерностью вращения (изменением $\omega$ по величине)

$a_{вр} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times r = \varepsilon\times {\displaystyle \bf r},$

(1.25)

и центростремительного (нормального) ускорения

${\displaystyle \bf a}_{n} = \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}}}{\displaystyle {\displaystyle dt}}} = \omega\times \left( {\displaystyle \omega\times {\displaystyle \bf r}} \right) = - \omega^{2}\rho,$

(1.26)

где $\rho = \rho\left( {\displaystyle t} \right)$ - радиус-вектор, проведенный от мгновенной оси вращения в рассматриваемую точку. Здесь следует помнить, что угловое ускорение $\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}$ связано с изменением угловой скорости не только по величине, но и по направлению, так что $\bf a}_{вр$ и $\bf a}_{n$ не перпендикулярны друг другу.

Проекции вектора мгновенной угловой скорости $\omega$ на оси системы xyz, жестко связанной с твердым телом, можно выразить через углы Эйлера $\varphi , \psi , \theta$ (см. Рис. 1.3) и их производные по времени $\dot {\displaystyle \varphi }, \dot {\displaystyle \psi }, \dot {\displaystyle \theta }.$ Действительно, вектор $\omega$ можно представить в виде суммы трех составляющих:

$\omega = \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} + \dot {\displaystyle \psi } {\displaystyle \bf e}_{z_{o}} + \dot {\displaystyle \theta } {\displaystyle \bf e}_{OA} .$

(1.27)

Здесь $\bf e}_{z$ и $\bf e}_{z_{0}$ - единичные векторы вдоль осей Oz и Oz₀ соответственно, $\bf e}_{OA$ - единичный вектор вдоль линии узлов OA (на рис. 1.3 эти орты не показаны). Определим проекции векторов $\dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} , \dot {\displaystyle \psi } {\displaystyle \bf e}_{z_{o}} , \dot {\displaystyle \theta } {\displaystyle \bf e}_{OA},$ входящих в (1.27), на оси системы xyz (см. рис. 1.3):

$\left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{x} = 0; \quad \left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{y} = 0; \quad \left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{z} = \dot {\displaystyle \varphi };$

(1.28)

$\left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{x} = \dot {\displaystyle \psi } \sin \theta \cdot \sin \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{y} = \dot {\displaystyle \psi } \sin \theta \cdot \cos \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{z} = \dot {\displaystyle \psi } \cos \theta ;$

(1.29)

$\left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{x} = \dot {\displaystyle \theta }\cos \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{y} = - \dot {\displaystyle \theta }\sin \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{z} = 0.$

(1.30)

Из (1.27 - 1.30) получим:

$\omega _{x} = \dot {\displaystyle \psi }\sin \theta \sin \varphi + \dot {\displaystyle \theta }\cos\varphi ;$

(1.31)

$\omega _{y} = \dot {\displaystyle \psi }\sin \theta \cos \varphi - \dot {\displaystyle \theta }\sin\varphi ;$

(1.32)

$\omega _{z} = \dot {\displaystyle \varphi } + \dot {\displaystyle \psi }\cos \theta .$

(1.33)

Уравнения (1.31-1.33) называются кинематическими уравнениями Эйлера. Они, в частности, позволяют определить величину и направление вектора мгновенной угловой скорости $\omega,$ если закон движения тела задан в виде (1.22).

В ряде случаев вращение тела с закрепленной точкой вокруг мгновенной оси удобно представить как суперпозицию двух вращений вокруг пересекающихся осей. В случае, изображенном на рис. 1.22, вершина конуса шарнирно закреплена в точке О; ось конуса горизонтальна, а основание конуса катится без проскальзывания по горизонтальной плоскости S. Вектор угловой скорости $\omega$ направлен вдоль мгновенной оси вращения ОМ (скорость точек О и М равна нулю); при движении конуса мгновенная ось вращения изменяет свое положение, описывая некоторую коническую поверхность с вершиной в точке О. Абсолютное вращение конуса с угловой скоростью $\omega$ можно представить в виде суммы

$\omega = \omega_{1} + \omega_{2} ,$

(1.34)

где $\omega_{1}$ - угловая скорость относительного вращения конуса вокруг собственной оси симметрии, $\omega_{2}$ - угловая скорость переносного вращения самой оси конуса вокруг вертикали. Если задана $\omega _{2} ,$ то

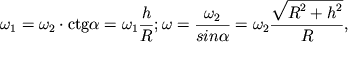$\omega _{1} = \omega _{2} \cdot {\displaystyle \rm ctg}\alpha = \omega _{1} {\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle R}}}; \omega = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{2} }}{\displaystyle {\displaystyle sin\alpha }}} = \omega _{2} {\displaystyle \frac{\displaystyle {\displaystyle \sqrt {\displaystyle R^{2} + h^{2}} }}{\displaystyle {\displaystyle R}}},$

где $\alpha$ - угол полураствора конуса, $R$ - радиус основания конуса, $h$ - его высота.

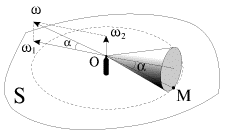Рис. 1.22.

Замечание. Движение тела, представляющее собой одновременное вращение вокруг нескольких осей с угловыми скоростями $\omega_{1} , \omega_{2} , \omega_{3} , \ldots$ может быть сведено к вращению вокруг одной оси с угловой скоростью

$\omega = \omega_{1} + \omega_{2} + \omega_{3} + \ldots,$

(1.35)

Движение свободного твердого тела.

Свободное твердое тело может совершать любые перемещения относительно лабораторной системы XYZ. В этом, самом общем случае, оно имеет 6 степеней свободы.

Опираясь на теорему Эйлера (см. выше), движение свободного твердого тела можно представить в виде суперпозиции поступательного движения, при котором все точки движутся как произвольно выбранный полюс (начало системы x₀y₀z₀) и вращательного движения вокруг мгновенной оси, проходящей через этот полюс. Этому рассмотрению соответствуют 6 независимых координат: 3 декартовы координаты X, Y, Z точки, принятой за полюс, и 3 угла Эйлера $\varphi , \psi , \theta$ (см. рис. 1.3).

Положение произвольной точки А тела в лабораторной системе XYZ определяется радиус-вектором $\bf r}_{A$ :

${\displaystyle \bf r}_{A} = {\displaystyle \bf r}_{O} + {\displaystyle \bf {\displaystyle r}'}_{A} ,$

(1.36)

где $\bf r}_{O$ - радиус-вектор точки О, принятой за полюс, ${\displaystyle \bf r}}'_{A$ - радиус-вектор точки А относительно полюса.

Скорость точки А

${\displaystyle \bf v}_{A} = {\displaystyle \bf v}_{O} + \omega\times {\displaystyle {\displaystyle \bf r}}'_{A} ,$

(1.37)

где $\bf v}_{O$ - скорость полюса, а $\omega\times {\displaystyle {\displaystyle \bf r}}'_{A}$ - линейная скорость вращательного движения вокруг оси, проходящей через полюс. Ускорение точки А

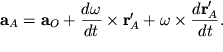${\displaystyle \bf a}_{A} = {\displaystyle \bf a}_{O} + {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}'_{A} + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{A} }}{\displaystyle {\displaystyle dt}}}.$

(1.38)

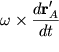Здесь $\bf a}_{O$ - ускорение полюса, $\frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}'_{A$ - ускорение, обусловленное изменением вектора мгновенной угловой скорости $\omega$ по величине и направлению, $\omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{A} }}{\displaystyle {\displaystyle dt}}}$ - центростремительное ускорение (см. формулу (1.26)).

Замечание 1. Принимая за полюс различные точки свободного твердого тела (или даже точки вне его), можно получить бесчисленное множество разложений его движения на поступательное и вращательное При этом, как и в случае плоского движения, кинематические характеристики переносного поступательного движения $\bf v}_{O}, {\displaystyle \bf a}_{O$ будут зависеть от выбора полюса. Кинематические же характеристики относительного вращательного движения $\omega, {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}$ от выбора полюса на зависят.

Замечание 2. Произвольное (неплоское) движение твердого тела невозможно свести к чистому вращению вокруг мгновенной оси. Однако можно показать, что в этом случае существует мгновенная ось так называемого винтового перемещения твердого тела. Произвольное движение твердого тела в XYZ в любой момент времени можно представить в виде суперпозиции вращательного движения вокруг некоторой оси и поступательного перемещения вдоль этой же самой оси. Естественно, с течением времени положение мгновенной оси винтового перемещения в пространстве и относительно тела в общем случае изменяется.

Назад| Вперед