Астронет > Механика твердого тела. Лекции.

Астронет: Физический факультет МГУ Механика твердого тела. Лекции.
http://variable-stars.ru/db/msg/1175788/page3.html

Механика твердого тела. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 1997 г. Содержание

Плоское движение.

Плоское движение - это такое движение твердого тела, при котором траектории всех его точек лежат в параллельных плоскостях. Если в теле провести некоторую прямую O₁O₂, перпендикулярную этим плоскостям (рис. 1.9), то все точки этой прямой будут двигаться по одинаковым траекториям с одинаковыми скоростями и ускорениями; сама прямая будет, естественно, сохранять свою ориентацию в пространстве. Таким образом, при плоском, или, как его иногда называют, плоско-параллельном, движении твердого тела достаточно рассмотреть движение одного из сечений тела.

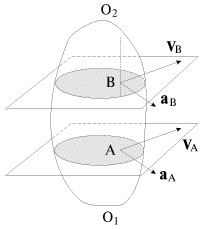Рис. 1.9.

Обратимся к классическому простому примеру плоского движения - качению цилиндра по плоскости без проскальзывания. Рассматривая одно из сечений цилиндра плоскостью, перпендикулярной его оси, мы придем к известное задаче о катящемся колесе (рис. 1.10). Центр колеса движется прямолинейно, траектории других точек представляют собой кривые, называемые циклоидами.

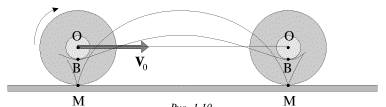Рис. 1.10.

При отсутствии проскальзывания мгновенная скорость самой нижней точки колеса (точки M) равна нулю. Это позволяет рассматривать качение колеса как суперпозицию двух движений: поступательного со скоростью оси $v_{0}$ и вращательного с угловой скоростью $\omega = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle R}}},$ где $R$ - радиус колеса. Ясно, что в этом случае $v_{M} = v_{0} - \omega R = 0.$

Попробуем обобщить этот прием на произвольное плоское движение.

Выделим отрезок АB в рассматриваемом сечении твердого тела (рис. 1.11). Перевод сечения из положения 1 в положение 2 можно рассматривать как суперпозицию двух движений: поступательного из 1 в 1' и вращательного из 1' в 2 вокруг точки A', называемой обычно полюсом (рис. 1.11а). Существенно, что в качестве полюса можно выбрать любую точку, принадлежащую сечению или даже лежащую в плоскости сечение вне его. На рис. 1.11б, к примеру, в качестве полюса выбрана точка В. Обратите внимание: длина пути при поступательном перемещении изменилась (в данном случае увеличилась), но угол поворота остался прежним!

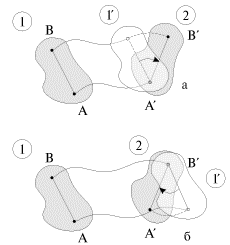Рис. 1.11.

Приближая конечное положение тела к начальному (сокращая рассматриваемый промежуток времени), приходим к выводу: плоское движение твердого тела в любой момент времени можно представить как суперпозицию поступательного движения со скоростью некоторой точки, выбранной в качестве полюса, и вращения вокруг оси, проходящей через полюс. В реальной ситуации оба эти движения, естественно, происходят одновременно. Существенно, что разложение на поступательное и вращательное движения оказывается неоднозначным, причем в зависимости от выбора полюса скорость поступательного движения будет изменяться, а угловая скорость вращения останется неизменной.

В соответствии со сказанным скорость любой точки А тела (рис. 1.12) геометрически складывается из скорости какой-либо другой точки O, принятой за полюс, и скорости вращательного движения вокруг этого полюса. Напомним, что система координат XYZ на рис. 1.12 - неподвижная (лабораторная); начало системы x₀y₀z₀ помещено в некоторую точку О тела (полюс), а сама система x₀y₀z₀ движется относительно XYZ поступательно, причем так, что оси Oy₀ и Oz₀ остаются в плоскости рисунка. Рассматриваемая точка А тела также движется в плоскости рисунка (плоское движение!).

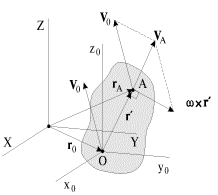Рис. 1.12.

Радиус-вектор точки А

${\displaystyle \bf r}_{A} = {\displaystyle \bf r}_{0} + {\displaystyle {\displaystyle \bf r}}'$

(1.15)

Скорость точки А

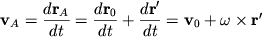${\displaystyle \bf v}_{A} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{A} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{0} }}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf v}_{0} + \omega\times {\displaystyle {\displaystyle \bf r}}'$

(1.16)

Из (1.16) можно сделать вывод, что в любой момент времени должна существовать такая точка M, скорость которой в лабораторной системе XYZ равна нулю - для этой точки

${\displaystyle \bf v}_{0} = - \omega\times {\displaystyle {\displaystyle \bf r}}'$

(1.17)

(рис. 1.13). Заметим, что эта точка не обязательно должна принадлежать телу, то есть может находиться и вне его. Таким образом, плоское движение твердого тела в данный момент времени можно представить как чистое вращение вокруг оси, проходящей через точку M - такая ось называется обычно мгновенной осью вращения. В частности, для колеса, катящегося по плоскости без проскальзывания (рис. 1.10), мгновенная ось вращения проходит через точку М соприкосновения колеса с плоскостью.

Рис. 1.13.

Существенно, что в разные моменты времени мгновенная ось вращения проходит через разные точки твердого тела и через разные точки лабораторной системы XYZ, сохраняя, конечно, свою ориентацию в пространстве.

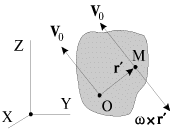
Для того, чтобы определить положение мгновенной оси вращения, необходимо знать скорости каких-либо двух точек твердого тела. Так, на рис. 1.14 показано положение мгновенной оси вращения (точка М) для цилиндра, зажатого между двумя параллельными рейками, которые движутся в одну и ту же сторону с разными скоростями $\bf v}_{1$ и ${\displaystyle \bf v}_{2}.$

Рис. 1.14.

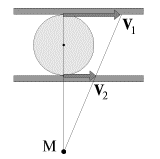
В ситуации, изображенной на рис. 1.15, стержень AB опирается на точку С и движется в плоскости чертежа так, что его конец B все время находится на полуокружности CBD При этом мгновенная ось вращения стержня (точка М) находится на верхней полуокружности CMD и при движении точки B вправо перемещается по дуге этой полуокружности влево.

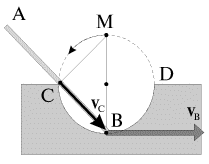Рис. 1.15.

В случае, показанном на рис. 1.16, стержень, опирающийся одним из своих концов на гладкую горизонтальную плоскость, начинает падать из вертикального положения. При этом центр масс стержня опускается, оставаясь на одной и той же вертикали. Мгновенная ось вращения (точка М) перемещается по дуге окружности радиуса $\frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}$ ( $\ell$ - длина стержня).

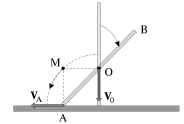Рис. 1.16.

Зная угловую скорость $\omega$ и положение мгновенной оси вращения, можно легко определить скорость любой точки тела при его плоском движении. Так, в случае колеса, катящегося по плоскости со скоростью $v_{0}$ без проскальзывания (рис. 1.17), скорость точки В

$v_{B} = \omega \cdot MB = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle R}}} \cdot MB;$

(1.18)

вектор $\bf v}_{B$ перпендикулярен отрезку в МВ, соединяющему точку В с точкой М, через которую проходит мгновенная ось вращения. Естественно, $\bf v}_{B$ можно представить и как геометрическую сумму двух скоростей: $\bf v}_{0$ - скорости поступательного движения оси колеса и ${\displaystyle \bf v}}'_{0$ - скорости вращательного движения вокруг этой оси, причем ${\displaystyle \left| {\displaystyle {\displaystyle \bf v}_{0} } \right|} = {\displaystyle \left| {\displaystyle {\displaystyle {\displaystyle \bf v}}'_{0} } \right|}.$ (рис. 1.17).

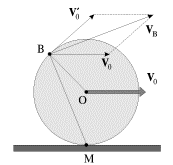Рис. 1.17.

Рис. 1.18 иллюстрирует распределение скоростей на вертикальном диаметре колеса железнодорожного вагона. Мгновенная ось вращения проходит через точку М соприкосновения колеса с рельсом. Хорошо видно, что линейная скорость точки на краю реборды направлена в сторону, противоположную движению вагона.

Рис. 1.18.

Определим теперь ускорения точек тела при плоском движении. Дифференцируя выражением (1.16) по времени, получим для ускорения точки А

$\bf a}_{A} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{A} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{0} }}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}' + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf a}_{0} + {\displaystyle \bf a}_{\tau } + {\displaystyle \bf a}_{n$

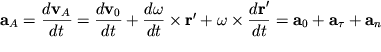(1.19)

Это ускорение складывается из трех частот (рис. 1.19): ускорения $\bf a}_{0$ точки O, принятой за полюс, тангенциального ускорения

${\displaystyle \bf a}_{\tau} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}' = \varepsilon\times {\displaystyle {\displaystyle \bf r}}'$

(1.20)

и нормального ускорения

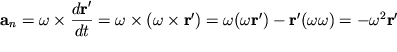${\displaystyle \bf a}_{n} = \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = \omega\times (\omega\times {\displaystyle {\displaystyle \bf r}}') = \omega (\omega {\displaystyle {\displaystyle \bf r}}') - {\displaystyle {\displaystyle \bf r}}'(\omega \omega) = - \omega ^{2}{\displaystyle {\displaystyle \bf r}}'$

(1.21)

(скалярное произведение $(\omega {\displaystyle r}')$ равно нулю, так как $\omega \bot {\displaystyle {\displaystyle \bf r}}'$ ).

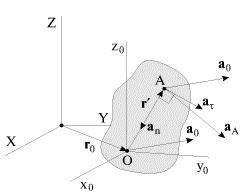Рис. 1.19.

Таким образом, ускорение любой точки А тела при плоском движении равно геометрической сумме ускорения точки, принятой за полюс, и ускорения точк, принятой за полюс, и ускорения точки A за счет ее вращения вокруг этого полюса. Отсюда, в частности, следует, что ускорение любой точки колеса, катящегося без проскальзывания по плоскости с постоянной скоростью $v_{0}$ , направлено к центру колеса и равно ${\displaystyle \frac{\displaystyle {\displaystyle v_{0} ^{2}}}{\displaystyle {\displaystyle r}}},$ где $r$ - расстояние рассматриваемой точки до центра колеса. 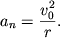В этом примере в качестве полюса удобно выбрать центр колеса О, тогда $a_{0} = a_{\tau } = 0,$ и остается только $a_{n} = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} ^{2}}}{\displaystyle {\displaystyle r}}}.$

Замечание. По аналогии с мгновенной осью вращения можно ввести мгновенную ось, ускорения всех точек которой в данный момент времени равны нулю. При этом следует иметь в виду, что эта ось, вообще говоря, не совпадает с мгновенной осью вращения. Так, в примере с колесом, катящимся по плоскости с постоянной скоростью, она проходит через центр колеса.

Назад| Вперед