Астронет > Динамическая голография и проблема обращения волнового фронта

Астронет: СОЖ Динамическая голография и проблема обращения волнового фронта
http://variable-stars.ru/db/msg/1175765/page1.html

Динамическая голография и проблема обращения волнового фронта

А. С. Чирцов (Санкт-Петербургский государственный университет)
Опубликовано в Соросовском образовательном журнале, N 1, 2001 г. Содержание

Введение. Постановка задачи

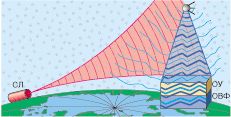
Методы динамической голографии при решении проблемы обращения волнового фронта являются красивым примером использования современных достижений физики и наукоемких технологий для решения весьма важной практической задачи фокусировки лазерного излучения на небольших объектах, перемещающихся в неоднородной и нестационарной оптической среде. Подобные задачи возникают, например, при попытках осуществления управляемого лазерного термоядерного синтеза, ключевой идеей которого является достижение необходимого для начала ядерной реакции разогрева дейтерий-тритиевой мишени (размер около 1 мм) путем ее облучения несколькими десятками синхронно срабатывающих сверхмощных импульсных лазеров.

Другим примером не менее сложной и одновременно практически важной задачи является наведение излучения расположенного на Земле лазера на движущийся спутник или самолет с целью эффективной передачи ему энергии или информации (использование лазеров для уничтожения летающих объектов не кажется слишком захватывающей проблемой не только по морально-этическим соображениям, но и из-за существования значительно более простых и эффективных методов ее решения). Проблема наведения лазерного луча в этом случае связана не столько с движением мишени, сколько с наличием неоднородной и постоянно изменяющейся во времени атмосферы Земли. Неизбежные статистические флуктуации плотности воздуха и как следствие - его показателя преломления неизбежно приводят к расфокусировке и рассеянию лазерного луча.

Читатель, не имеющий практического опыта работы с оптическими устройствами, даже на основании здравого смысла легко согласится с тем, что реализация описанных проектов методами классической оптики представляется достаточно проблематичным.

Идея решения - обращение волнового фронта

Обе сформулированные (и сходные с ними) проблемы могут быть сравнительно легко решены при наличии трех устройств: источника когерентного излучения (лазера), оптического усилителя и "зеркала", обращающего направление распространения излучения в пространстве, но не искажающего формы его волнового фронта. Рассмотрим идею основанного на использовании перечисленных устройств метода эффективной фокусировки на примере решения второй из перечисленных проблем - наведения лазерного излучения на движущееся тело, отделенное от лазера слоем неоднородной и нестационарной атмосферы (рис. 1).

Рис. 1. Использование ОВФ для наведения мощного лазерного излучения на мишень в условиях нестационарной атмосферы: СЛ - маломощный сигнальный лазер, ОУ - оптической усилитель, ОВФ - устройство, обеспечивающее быстрое обращение волнового фронта

Сравнительно маломощный лазер используется как источник подсвечивающего излучения и создает пучок, достаточно широкий для того, чтобы попадание в него мишени не составляло серьезных технических проблем. Отраженные от мишени световые волны распространяются во все стороны, в том числе и в направлении силовой оптической установки, содержащей оптический усилитель и устройство, осуществляющее обращение направления распространения световых волн. На пути к ней сигнальная волна может существенно исказиться на неоднородностях плотности атмосферы. Попавший на оптический усилитель участок искаженного волнового фронта многократно усиливается, не изменяя своей пространственной конфигурации. После обращения направления распространения и еще одного усиления он продолжает движение уже в направлении к мишени вновь через неоднородности флуктуирующей атмосферы. Если обращение волнового фронта осуществляется быстрее, чем характерное время изменения микросостояния атмосферы (задержки, связанные с конечной скоростью распространения света, оказываются существенно меньшими), возвращаемый силовой установкой мощный импульс излучения пройдет через те же неоднородности, что и сигнальный. Из известного из геометрической оптики свойства обратимости хода световых лучей следует, что, приближаясь к мишени, импульс будет постепенно восстанавливать свою исходную пространственную конфигурацию и как следствие - полностью соберется на поверхности мишени.

На этом наиболее интригующая часть рассказа об обращении волнового фронта подходит к концу, и читатель, интересующийся лишь эффектными применениями достижений современной науки на практике, может смело переходить к поиску интересного для него материала. Оставшаяся часть статьи адресована тем, кто, получив ответ на вопрос, КАК СДЕЛАТЬ, заинтересовался проблемой, ПОЧЕМУ ТАК ПРОИСХОДИТ, и готов затратить определенные усилия на осмысление весьма нетривиальных физических принципов, лежащих в основе работы устройств, обеспечивающих обращение волнового фронта (ОВФ). До сравнительно недавнего времени указанный круг проблем по понятным причинам не обсуждался в открытой печати и потому не столь широко известен, как, например, принципы действия лазеров и оптических усилителей (желающим углубить свои знания в этих вопросах можно рекомендовать обзор [Собельман И.И., 1969] или соответствующие разделы учебников [Сивухин Д.В., 1985] или [Бутиков Е.И., 1986]). При этом идеи голографического обращения волнового фронта [Зельдович Б.Я., Пилипецкий Н.Ф., Шкунов В.В., 1985] настолько изящны и неожиданны, что, несомненно, привлекут внимание интересующегося точными науками читателя.

Теорема Фурье и плоские монохроматические волны

В большинстве элементарных курсов физики свет обычно рассматривается как совокупность электромагнитных волн. При этом чаще всего подразумеваются плоские монохроматические волны, представляющие собой лишь один из наиболее простых для анализа типов волновых процессов. Напомним кратко основные свойства таких волн.

Плоскую монохроматическую электромагнитную волну в вакууме (рис. 2) можно представить себе как непрерывно заполняющее все пространство множество параллельных плоскостей (волновых фронтов), во всех точках которых лежат описывающие электрическое и магнитное поле векторы E и B. Величины этих векторов на каждой из таких плоскостей одинаковы, а их направления взаимно перпендикулярны. Описанный бесконечный слоеный пирог несется со скоростью света c в перпендикулярном волновым фронтам направлении, которое принято задавать при помощи волнового вектора $\bar{k}$ . Его величина связана с длиной волны $\lambda$ и частотой света w соотношением

$|\bar{k}| = \displaystyle{\frac{2\pi}{\lambda}} = \displaystyle{\frac{w}{c}}$ .

(1)

Вдоль задаваемого волновым вектором $\bar{k}$ направления величины векторов $\bar{E}$ и $\bar{B}$ изменяются по гармоническому закону (то есть как синус или косинус).

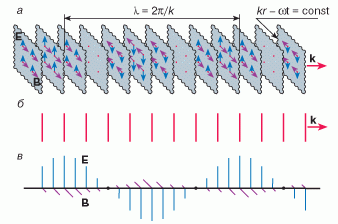Рис. 2.Плоские монохроматические волны: а - не очень удачная попытка изобразить электромагнитное поле, описываемое только одним слагаемым разложения [Вишик М.И., 1997.]; б - упрощенное изображение плоской монохроматической волны, используемое в дальнейших рисунках; в - традиционное изображение электромагнитной волны, используемое в большинстве учебников

Являющиеся одним из возможных решений уравнений Максвелла для поля в вакууме плоские волны в чистом виде в природе не встречаются. Некоторые источники света (лазеры) могут создавать поля, приближенно описываемые при помощи отдельных плоских монохроматических волн. В этом смысле плоские волны в оптике аналогичны материальным точкам в механике: и те и другие являются допускающими удобное математическое описание заведомо упрощенными образами реальных физических объектов. Однако этим значение плоских монохроматических волн для физики не исчерпывается.

В начале XIX века французский математик Ж. Фурье развил чрезвычайно мощный метод, в основе которого лежит представление периодических функций при помощи тригонометрических рядов (в виде бесконечных сумм по дискретному набору кратных частот синусов и косинусов). Такое представление функций во многом аналогично разложению вектора по ортонормированному базису [Вишик М.И., 1997.]. В дальнейшем оказалось, что достаточно гладкие непериодические функции, обращающиеся в нуль на бесконечности, также представимы суперпозицией тригонометрических функций, частоты которых в этом случае пробегают непрерывный набор значений (интеграл Фурье). Сформулированные утверждения имеют непосредственное отношение к проблеме обращения волнового фронта: реально существующее электромагнитное поле можно рассматривать как суперпозицию плоских монохроматических волн.

Назад | Вперед