 |
Астронет: Р. Е. Ильинский Наблюдение солнечных пятен с классической камерой обскурой: комментарий http://www.astronet.ru/db/msg/1174785/text |
15.02.2002 15:41 | Р. Е. Ильинский
Наблюдение солнечных пятен с классической камерой обскурой: комментарий
Р.Е. Ильинский
|
Данная статья является критическим комментарием серии статей В.Г.Сурдина. Одна из статей данной серии, давшая название и данной работе, "Наблюдение солнечных пятен с классической камерой-обскурой" [1], также опубликована на этом сайте. Редакция. |
За последние несколько лет В. Г. Сурдиным был опубликован ряд статей [1,2,3,4,5,6], где он высказал гипотезу об использовании в "дотелескопный" период безлинзовой камеры-обскуры (БЛКО) для наблюдения солнечных пятен и попытался подтвердить эту гипотезу экспериментально.
Прежде чем перейти к наблюдению солнечных пятен с помощью БЛКО В. Г. Сурдин в своей статье [1] утверждает, что глазом можно наблюдать только пятна размером " 3'-4', а рядовое солнечное пятно имеет угловой размер около 0.3' ", т. е. меньше 1' - предела разрешения нормального человеческого глаза. Подобное утверждение плохо согласуется с тем, что В. Г. Сурдин в созданной им БЛКО наблюдал солнечные пятна "диаметрами 15" и 17", разделенных расстоянием в 1' ", хотя "теоретическое разрешение нашей камеры около 40'' ". В [12] показано, что наблюдение прохождения планеты Меркурий (угловой размер 12") по диску Солнца лежит только немного за пределами возможностей человеческого глаза. Указанные факты подтверждают возможность наблюдения глазом солнечных пятен диаметром в 20"-30".
В. Г. Сурдин в своей статье [1] указал несколько известных ему фактов использования БЛКО для астрологических наблюдений в "дотелескопный" период. Гораздо более подробно об этом написано в книге [11]: в 1279 г. англичанин Джон Пенхам предложил использовать БЛКО для наблюдений за движением Солнца; в январе 1544 г. голландский математик Гемма Фризиус наблюдал с помощью камеры-обскуры солнечное затмение. Использовал камеру-обскуру (из [11] не совсем понятно была она с линзой или без) в своих астрологических исследованиях Кеплер. В 1607 г. он наблюдал с ее помощью прохождение Меркурием солнечного диска. В [11] указано, что в архиве АН СССР хранилось письмо тирольского художника М. Штольца, в котором он просит Кеплера высказать свое мнение о камере-обскуре, сконструированной автором письма для зарисовок с натуры.
В. Г. Сурдин в своей статье [1] пишет:
К сожалению, в русском языке под термином "камера-обскура" объединились два разных прибора: 1) классическая "темная коробка с маленьким отверстием", играющим роль примитивного объектива, и 2) проекционная линзовая камера, прототип фотокамеры. Такое смешение порой становится причиной казусных ситуаций в русскоязычной литературе, которых иногда удается избегать в английском языке, поскольку для классической безлинзовой камеры в нем применяется термин "pinhole camera", а ее аналог с линзовым объективом обычно называют "camera obscura".Интересно сравнить этот абзац с цитатой из статьи [9]:
Lensless imaging is known as the basis of the camera obscura, or pinhole imagery. (Безлинзовый изображающий прибор известен как основа "camera obscura" или "pinhole imagery".)Следовательно, и в английском языке термином "камера-обскура" могут называться как линзовые, так и безлинзовые устройства. Историкам науки желательно иметь это в виду.
Что касается камер-обскур, которые использовались в первых опытах по фотографии (о них упоминает в своих статьях В. Г. Сурдин), то тут не нужны никакие догадки. Типы камер основоположников фотографии Ньепса, Дагера и Талбота хорошо известны историкам науки [11]. Можно напомнить, что переписка Ньепса и Дагера была издана АН СССР [20].
Редко в каком начальном курсе оптики или популярной литературе на эту же тему не упоминается БЛКО. Гораздо реже дается правильное описание формирования изображения БЛКО. Уже одно то, что о БЛКО рассказывают в разделе "Прямолинейное распространение света" [16] вызывает, по меньшей мере, удивление. БЛКО является хотя и простейшим, но дифракционным элементом.
Коротко рассмотрим формирование изображения БЛКО для
случая, когда изображаемый предмет бесконечно удален от БЛКО.
Выберем на изображаемом объекте точку, которая находится на оси БЛКО
(т. е. лежит на прямой проходящей через центр круглого отверстия и
перпендикулярной плоскости наблюдения). Очевидно, что волновой фронт,
пришедший из выбранной точки на отверстие БЛКО, будет плоским и
перпендикулярным оси
БЛКО рис. 1. Далее задача становится классической:
дифракция
световой волны на круглом
отверстии. Разобьем поверхность отверстия на элементарные участки ![]() .
Каждый из этих участков, в соответствии с
принципом Гюйгенса-Френеля, будем рассматривать как новый источник,
испускающий сферическую волну. Просуммировав затем поля, создаваемые
участками
.
Каждый из этих участков, в соответствии с
принципом Гюйгенса-Френеля, будем рассматривать как новый источник,
испускающий сферическую волну. Просуммировав затем поля, создаваемые
участками ![]() в какой-либо точке
в какой-либо точке ![]() в плоскости наблюдения,
найдем суммарное распределение поля.
в плоскости наблюдения,
найдем суммарное распределение поля.
Поле, создаваемое источником ![]() в точке
в точке ![]() , пропорционально
амплитуде волны
, пропорционально
амплитуде волны ![]() на отверстии.
Поэтому поле, создаваемое в точке
на отверстии.
Поэтому поле, создаваемое в точке ![]() участком
участком ![]() , будет
пропорционально
, будет
пропорционально ![]() . Изменение амплитуды и фазы волны, проходящей
расстояние
. Изменение амплитуды и фазы волны, проходящей
расстояние ![]() от источника
от источника ![]() до точки наблюдения
до точки наблюдения ![]() , учтем
множителем
, учтем
множителем
![]() , где
, где ![]() -длина волны
излучения. Таким образом, каждый
из элементарных источников
-длина волны
излучения. Таким образом, каждый
из элементарных источников ![]() создает в точке
создает в точке ![]() поле
поле
где
Результирующее поле в точке ![]() , являющееся суммой элементарных полей
всех элементарных источников, будет равно
, являющееся суммой элементарных полей
всех элементарных источников, будет равно
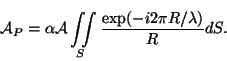
Интенсивность светового поля в точке
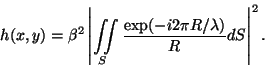
Множитель
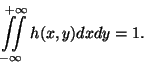
Функция
Что изменится в дифракционной картине для точки наблюдаемого объекта, смещенной с
оси БЛКО?
Волновой фронт в этом случае также будет плоским, но он будет падать на
отверстие БЛКО под углом ![]() рис. 2.
При не очень больших
рис. 2.
При не очень больших ![]() вид
дифракционной картины существенно не изменится, за исключением того, что ее
центр перейдет из точки
вид
дифракционной картины существенно не изменится, за исключением того, что ее
центр перейдет из точки ![]() в точку
в точку ![]() (
(
![]() )
[7,12].
С точностью до постоянного множителя вид дифракционной картины будет описываться
функцией
)
[7,12].
С точностью до постоянного множителя вид дифракционной картины будет описываться
функцией
![]() , где
, где ![]() ,
, ![]() - координаты точки
- координаты точки ![]() .
.
Если
![]() - угловое распределение яркости изображаемого объекта, то освещенность
в плоскости наблюдения равна
[18]
- угловое распределение яркости изображаемого объекта, то освещенность
в плоскости наблюдения равна
[18]
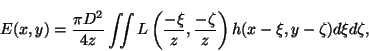
где
Распределение интенсивности в спектральном диапазоне
![]() ...
...![]() рассчитывается по формуле [18]
рассчитывается по формуле [18]

где весовая функция
Методы расчета дифракционных картин от отверстий различных форм были разработаны и экспериментально подтверждены в начале XIX века [24]. В это же время были найдены в аналитическом и полуаналитическом видах распределения интенсивности в дифракционных картинах от отверстий простейших геометрических форм. Интересующиеся читатели могут обратиться к статье [10], где дан краткий исторический очерк и приведены выражения для расчета дифракционных картин от прямоугольного и круглого отверстий.
В большинстве случаев считается оптимальной установка плоскости наблюдения БЛКО
на расстоянии
![]() от отверстия. Это связано с тем, что при этом значении
от отверстия. Это связано с тем, что при этом значении ![]() в точку
в точку ![]() колебания приходят
от элементарных площадок
колебания приходят
от элементарных площадок ![]() на отверстии с разностью не более
на отверстии с разностью не более ![]() .
Уменьшение расстояния
.
Уменьшение расстояния ![]() от этого значения приводит к появлению в точке
от этого значения приводит к появлению в точке ![]() колебаний с противофазой. Увеличение дистанции
колебаний с противофазой. Увеличение дистанции ![]() приводит к уменьшению
светосилы БЛКО.
Более подробно об определении оптимального расстояния
приводит к уменьшению
светосилы БЛКО.
Более подробно об определении оптимального расстояния ![]() , исходя из различных критериев, сказано в статье
[9]. В ней же дан исторический обзор работ по БЛКО.
, исходя из различных критериев, сказано в статье
[9]. В ней же дан исторический обзор работ по БЛКО.
На рис. 3 показан вид функции ![]() для
для
![]() мм,
мм,
![]() мм,
мм,
![]() . Указанные значения соответствуют опыту
В. Г. Сурдина в астрологическом институте имени П. К. Штернберга.
На рис. 4 показан график концентрации энергии
в изображении точки. Для
сравнения на этих рисунках приведены графики, рассчитанные в геометрическом
приближении. Анализ полученных графиков показывает, что дифракция приводит к
существенному перераспределению энергии в пятне рассеяния. Причем не только
к "размытию" геометрического пятна, но и к увеличению (в 4 раза) интенсивности
в центре пятна рассеяния. Поэтому тезис о том, "что оба указанных эффекта -
геометрический
размер пучка и дифракция - действуют независимо" [1]
нельзя признать верным как для БЛКО, так и для большинства оптических систем
[7,12].
Косвенно это подтверждают и данные статьи [2], где
измеренное разрешение БЛКО оказалось лучше "теоретического".
. Указанные значения соответствуют опыту
В. Г. Сурдина в астрологическом институте имени П. К. Штернберга.
На рис. 4 показан график концентрации энергии
в изображении точки. Для
сравнения на этих рисунках приведены графики, рассчитанные в геометрическом
приближении. Анализ полученных графиков показывает, что дифракция приводит к
существенному перераспределению энергии в пятне рассеяния. Причем не только
к "размытию" геометрического пятна, но и к увеличению (в 4 раза) интенсивности
в центре пятна рассеяния. Поэтому тезис о том, "что оба указанных эффекта -
геометрический
размер пучка и дифракция - действуют независимо" [1]
нельзя признать верным как для БЛКО, так и для большинства оптических систем
[7,12].
Косвенно это подтверждают и данные статьи [2], где
измеренное разрешение БЛКО оказалось лучше "теоретического".
 |
| Рис. 3. Распределение энергии в пятне рассеяния: 1 - с учетом дифракции, 2 - геометрическое приближение. |
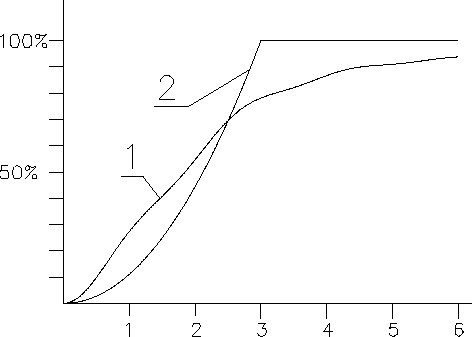 |
| Рис. 4. Концентрация энергии в пятне рассеяния: 1 - с учетом дифракции, 2 - геометрическое приближение. |
На протяжении XIX-XX веков БЛКО и неразрывно связанным с ней вопросами дифракции света уделили внимание лорд Рэлей [21], Петцваль [23], Р. Вуд и многие другие физики и оптики. Следует упомянуть статью [17], где описана весьма нетрадиционная БЛКО. За последние годы словосочетание "камера-обскура" стало заметно чаще встречаться на станицах научных журналов в связи с так называемым "дифракционным сдвигом изображения" [19]. БЛКО в ее "классическом" варианте продолжает применяться в целом ряде оптических приборов, где использование традиционных линз и зеркал невозможно или нежелательно: фокусировка ультрафиолетового и рентгеновского излучения, фотометрия [9]. Одно из последних изобретений в области "камеры-обскуры" - дифракционные очки [25].
За последние 30 лет фокусирующие дифракционные элементы - далекие потомки БЛКО - сделали огромный шаг вперед [8,13]. Это связано с развитием лазерной техники и голографии, появлением высокоразрешающего фотолитографического оборудования, потребностью в создании высокоэффективных систем для ультрафиолетового и рентгеновского диапазонов спектра. Отверстие в БЛКО можно рассматривать как зонную пластинку с единственной прозрачной зоной [8]. Зонная пластинка авторами учебников совершенно справедливо помещается в раздел "Дифракция" [15], но БЛКО теми же авторами заносится в раздел "Прямолинейное распространение света" [16]. Дело доходит до курьезов [14]: в начале статьи БЛКО приводится как пример прямолинейного распространения света, а в конце статьи дан рисунок, на котором показана схема фокусировки отверстием расходящейся волны. Скорее всего, все дело в традиции, берущей свое начало еще от манускриптов средневековья.
Литература
1 Сурдин В.Г., Наблюдение солнечных пятен с классической камерой-обскурой// Вопросы истории естествознания и техники. 2000. 4.2 Сурдин В. Г., Карташев М. А. Камера-обскура// Квант. 1999. 2.
3 Сурдин В.Г. Камера-обскура: упущенная возможность древних астрономов?// Звездочет. 1998. 10.
4 Сурдин В.Г. Солнечные пятна и камера-обскура// Земля и Вселенная. 1999. 1.
5 Сурдин В.Г. Готический храм -- солнечная обсерватория// Звездочет. 1999. 1.
6 Сурдин В.Г. Готический храм как солнечная обсерватория // Земля и Вселенная. 1999. 5.
7 Борн М., Вольф Э. Основы оптики.- М.: Наука, 1970.-856с.
8 Грейсух Г.И., Ефименко И. М., Степанов С. А. Оптика градиентных и дифракционных элементов. - М.: Радио и связь, 1990.-136с.
9 Klaus D. Mielenz On the Diffraction Limit for Lensless Imaging// Journal of Research of the National Institute of Standards and Technology. Volume 104, 5, 1999. p.479 -485.
10 Klaus D. Mielenz Algorithms for Fresnel Diffraction at Rectangular and Circular Apertures// Journal of Research of the National Institute of Standards and Technology. Volume 103, 5, 1998. p.497 - 509.
11 И. А. Головня С чего начиналась фотография.- М.: Знание, 1991.- 176 с.
12 А. Марешаль, М. Франсон Структура оптического изображения.- М.: Мир,1961.- 296 с.
13 Степанов С. А. Расчет и анализ оптических систем, включающих дифракционные и градиентные элементы. Автореферат диссертации на соискание ученой степени доктора физико-математических наук.- Самара. 1998.-32с.
14 Г. Косоуров Шарик вместо линзы.// Опыты в домашней лаборатории. Библиотечка "Квант" М. 1981. с.134-143.
15 Ландсберг Г. С. Оптика.- М.: Наука,1976.- 927 с.
16 Ландсберг Г. С. Элементарный учебник физики. т.3. Колебания и волны. Оптика. Строение атома.- М.: Государственное издательство технико-теоретической литературы.,1952.
17 R. W. Wood Fish-Eye Views, and Vision under Water.// Philosophical Magazin Volume 12 68 1906 p.159-162
18 Г. М. Мосягин, В. Б. Немтинов, Е. Н. Лебедев Теория оптико-электронных систем.- М.: Машиностроение,1990.- 432 с.
19 И. Г. Пальчикова, С. Г. Раутиан Дифракционный сдвиг изображения// Оптика и спектроскопия. 1999. т. 87 3 с.510-519.
20 Документы по истории изобретения фотографии./ Под ред. Т.П.Кравеца- Л.: Изд-во АН СССР,1967.
21 Lord Rayleigh Wave Theory of Light, Enc. Brit. 24, 91 (1888).
22 Lord Rayleigh On Pinhole Photography. Scientific Papers III. Cambridge U. Press 1902 p. 492-440.
23 J. M. Petzval, Wiener Akad. Ber. 26, 33 1857.
24 A. Fresnel Memoir on the Diffraction of Light, Paris 1819.
25 В. П. Бессмельцев, С. Г. Баев, И. Г. Пальчикова Растровые дифракционно-апертурные очки// Автометрия 1997. /No 6 с.57-66

