Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect4-5.html

Механика сплошных сред

Эффект Магнуса.

Если расположить цилиндр поперек потока, то на него будет действовать сила лобового сопротивления. Однако если цилиндр привести во вращение вокруг своей оси, то появится также и подъемная сила. В этом легко можно убедиться, если пронаблюдать за траекторией падающего легкого пенопластового цилиндра, предварительно скатившегося с наклонной плоскости (рис. 4.32). Цилиндр стремится упасть под стол, что свидетельствует о наличии силы F, направленной перпендикулярно скорости движения оси цилиндра. Эта сила появляется вследствие вращения цилиндра в вязком воздухе, а само явление называется эффект Магнуса.

Рис. 4.32.

При вращении цилиндра воздух в пограничном слое увлекается поверхностью цилиндра. Обтекание вращающегося цилиндра будет выглядеть так, как показано на рис. 4.33. Скорость воздушного потока над цилиндром будет больше, чем под ним. Величина силы F, как показывает расчет, увеличивается как с увеличением скорости потока, так и с угловой скоростью вращения цилиндра. Эффект Магнуса не получил широкого технического применения, хотя предпринимались попытки заменить паруса кораблей вращающимся цилиндром (ротором Флеттнера). Однако в спортивных играх с мячом последний часто подкручивают, чтобы задать полету мяча нужную траекторию.

Рис. 4.33.

Экранный эффект.

Этот эффект заключается в увеличении подъемной силы, а также в снижении лобового сопротивления на высотах, соизмеримых с длиной хорды крыла летательного аппарата. Прирост подъемной силы крыла вблизи ровного участка Земли или поверхности воды (экрана) вызывается повышением динамического давления на нижней поверхности крыла вследствие близости экрана. Снижение лобового сопротивления связано с уменьшением вихреобразований около концов крыльев (уменьшением индуктивного сопротивления). Первыми начали изучать экранный эффект судостроители. Шведский ученый Э. Сведберг в 1716 г. предложил идею использования "воздушной подушки" для уменьшения сопротивления движению судов. Впоследствии эта идея нашла воплощение при строительстве экранопланов - воздушных судов, летающих вблизи экрана. Первый экспериментальный экраноплан был построен в 1935 г. финским инженером Т. Каарно. Однако разработка и производство экранопланов, не имеющих мировых аналогов, получили широкое развитие в 80-е годы в СССР. Полет экраноплана "Лунь" (декабрь 1989 г.) показан на фотографии (рис. 4.34). Экраноплан соединяет в себе положительные качества самолетов и кораблей, что позволяет использовать его для перевозки пассажиров и грузов, поисково-спасательных работ, военных целей и др. Скорость их движения при полете у экрана составляет 400-550 км/ч, при полете вне экрана - до 750 км/ч; высота полета вне экрана -до 7500 м; мореходность при посадке в море - до 5 баллов (высота волны до 3,5 м). Экраноплан может принять на борт до 800 человек.

Рис. 4.34.

Сверхзвуковое обтекание тел.

Обтекание тела воздушным потоком, скорость которого превышает скорость звука в воздухе, имеет ряд специфических свойств. Рассмотрим вначале обтекание сильно вытянутого вдоль потока тела, напоминающего иглу (рис. 4.35). В непосредственной близости перед острием в т. О возникает возмущение плотности воздуха $\Delta\rho>0$ . Это возмущение в неподвижном воздухе распространялось бы в виде сферических волн, радиус которых R увеличивался бы во времени: R=ct. В сверхзвуковом потоке эти возмущения будут сноситься потоком и оставаться внутри конуса возмущений - конуса Маха с углом $\sin\alpha=c/v<1$ .

Рис. 4.35.

Воспользуемся принципом обратимости движения, согласно которому, обтекание жидкостью тела эквивалентно движению тела в покоящейся жидкости. С учетом этого можно сказать, что при движении тела со сверхзвуковой скоростью возбуждаются возмущения плотности и давления, локализованные на поверхности движущегося с телом конуса Маха. Когда это возмущение достигает неподвижных частиц воздуха, то последние получают воздействие, подобное удару, и приходят в движение. Поэтому возмущение носит название ударной волны. При обтекании сверхзвуковым потоком конического тела (рис. 4.36а) линии тока как бы "преломляются" на поверхности уплотнений воздуха. Для классификации течения вводят число Маха M=v/c. Оно равно отношению скорости течения к скорости звука в данном месте течения. В невозмущенном сверхзвуковом потоке М>1. На поверхности конуса Маха из-за повышения плотности скорость звука возрастает, и М = 1. У поверхности конуса воздух разрежен и его обтекание носит дозвуковой характер (М<1). При обтекании тела с затупленной частью скачок уплотнений становится криволинейным и отходит от тела (рис. 4.36б).

Рис. 4.36.

На образование ударных волн расходуется кинетическая энергия движущегося тела, поэтому даже в отсутствие вязкости при сверхзвуковых скоростях возникает значительная сила лобового сопротивления. Эта сила существенно зависит от формы головной части движущегося тела. Например, игла (рис.4.37), помещенная перед цилиндрическим телом, как бы рассекает поток, способствуя отрыву потока от поверхности цилиндра. Этот отрыв потока приводит к уменьшению лобового сопротивления движущегося цилиндра. Этой же цели служит использование стреловидных (скошенных) и треугольных крыльев на сверхзвуковых самолетах.

Рис. 4.37.

Отдельно следует упомянуть об обтекании с гиперзвуковой скоростью, когда число Маха М $\gg$ 1. Полет тел в газе с такими скоростями (спускаемых космических аппаратов, например) связан с ростом до очень больших значений температуры газа вблизи поверхности тела. Это обусловлено адиабатическим нагревом сжимаемого воздуха перед головной частью тела и выделением теплоты вследствие вязкого трения. 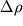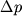При изучении гиперзвуковых течений необходимо не только учитывать сжимаемость воздуха, но и нелинейный характер его движения, так как возмущения плотности $\Delta\rho$ и давления $\Delta p$ не могут рассматриваться малыми по сравнению с равновесными значениями плотности $\rho_0$ и давления p₀ воздуха. Помимо этого, при высоких температурах необходимо учитывать и изменение физико-химических свойств воздуха. Мы лишь ограничимся одним важным выводом из такого анализа. При очень больших числах Маха давление воздуха непосредственно перед головной частью может быть пренебрежимо малым по сравнению с давлением воздуха перед ударной волной, где М $\gg$ 1. На рис. 4.38 представлен экспериментально полученный график коэффициентов лобового сопротивления для тел в виде сферы и цилиндра с конической головной частью. Хорошо видно, что в силу вышеуказанного падения давления перед головной частью коэффициенты лобового сопротивления убывают с ростом М, а начиная с М = 4 меняются мало и сравнимы со значениями коэффициентов при дозвуковых течениях.

Рис. 4.38.

При сверхзвуковых скоростях меняется картина обтекания крыла самолета. Сверху над крылом течение отрывается от его поверхности, а под крылом происходит скачок плотности. При таком обтекании, как показывает анализ, величина подъемной силы может быть грубо оценена с использованием ударной теории Ньютона, в которой $F_\perp\sim \sin^2\alpha$ . Одним из уникальных достижений современной аэродинамики является создание в России в 1997 г. новейшего истребителя СУ-37, у которого впервые в мире использованы крылья с отрицательной стреловидностью. Контур этого самолета изображен на рис. 4.37. Такой самолет имеет меньшее аэродинамическое сопротивление, чем самолет с обычным стреловидным крылом. Помимо этого у него увеличенная подъемная сила на малых и высоких скоростях и уникальные взлетно-посадочные характеристики.

Рис. 4.39.

Экспериментальные аэродинамические исследования.

Взаимодействие летательных аппаратов с потоком воздуха изучают экспериментально в ходе летных испытаний. Для этого на борт аппарата устанавливается разнообразная аппаратура, фиксирующая аэродинамические нагрузки. Однако значительно больший объем информации удается получить при обдувании потоком воздуха летательного аппарата в натуральную величину или его уменьшенной геометрической копии (модели). Это осуществляется в аэродинамических трубах, схема которой изображена на рис. 4.40.

Рис. 4.40.

В замкнутом канале переменного сечения с помощью мощного вентилятора 1 создается поток воздуха в направлении, указанном стрелками. В узкой части канала (в сопле), где скорость потока наибольшая, помещается исследуемый объект 2 (или его модель). Этот объект связан с аэродинамическими весами 3, позволяющими измерять аэродинамические силы и моменты сил, действующие на объект. Кроме труб с замкнутым циклом существуют разомкнутые аэродинамические трубы, в которые газ подводится из специальных емкостей. Аэродинамическая труба для экспериментов с натуральными объектами является громадной, сложной и чрезвычайно дорогостоящей экспериментальной установкой. Первая аэродинамическая труба в мире была создана в 1897 г. К.Э. Циолковским при поддержке Н.Е. Жуковского. В ней он провел исследования моделей дирижаблей и самолетов в потоке, скорость которого была около 5 м/с. В 1902 г. Н.Е. Жуковский построил при механическом кабинете Московского университета первую аэродинамическую трубу с электрическим приводом. В 1904 г. под его руководством был создан первый в мире аэродинамический институт (ЦАГИ), оказавший огромное влияние на развитие авиации и космонавтики. В настоящее время в мире существуют уникальные аэродинамические трубы, позволяющие проводить испытания летательных аппаратов в натуральную величину при сверхзвуковых скоростях потоков. В менее дорогостоящих экспериментах с моделями возникает проблема перенесения результатов эксперимента на натуральные объекты. Ясно, что модель должна быть точной уменьшенной геометрической копией натурального объекта. Если, например, бугорки поверхности крыла реального самолета достигают нескольких микрон, то у модели, уменьшенной в 10 раз, крылья должны быть отполированы до долей микрона. Однако лишь геометрического подобия недостаточно. Надо также создать такие условия обтекания, при которых соотношение между силами инерции, давления и вязкости в модельных и натуральных условиях было бы одинаковым. Для дозвуковых скоростей критерием подобия натурных и модельных экспериментов является равенство чисел Рейнольдса в обоих случаях:

${\rm Re}=\frac{\rho_м v_м \ell_м}{\mu_м}= \frac{\rho_н v_н \ell_н}{\mu_н}.$

(4.52)

Здесь индексы "м" и "н" относятся к параметрам модельного и натурального экспериментов. Если, например, размер модели в 10 раз меньше размеров натурального объекта $(\ell_м = 0.1 \ell_н),$ то подобие обтекания может быть достигнуто либо 10-кратным увеличением скорости потока, либо таким же увеличением плотности воздуха. Второе чаще оказывается предпочтительнее, поскольку скорость vм не может превзойти скорость звука, когда картина становится принципиально другой. Поэтому в аэродинамических трубах воздух сжимается до давления несколько десятков атмосфер, что позволяет обеспечить условие (4.52). В качестве иллюстрации на рис. 4.41 показана распределение воздушных потоков, обдувающих модели зданий. Ясно, что такой эксперимент является чрезвычайно полезным при проектировке строительства зданий и расчете на них действующей ветровой нагрузки. При сверхзвуковых испытаниях модель помещается в сопло Лаваля, устанавливаемое в аэродинамической трубе. В этих трубах потери на образование ударных волн велики, поэтому используются мощные многоступенчатые компрессоры. Широкое распространение получили баллонные аэродинамические трубы, в которые воздух поступает из баллонов высокого давления (несколько тысяч атмосфер). В сверхзвуковом режиме помимо (4.52) необходимо выполнение и второго условия подобия - равенства чисел Маха:

M = v_м / c_м = v_н / c_н

(4.53)

Отметим, что в трубах, где М $\gg$ 1, возникает ряд технических проблем, связанных с предотвращением конденсации струи воздуха вследствие понижения температуры при прохождении через сопло Лаваля. С этой целью воздух предварительно подогревают до температур ~10³ К, либо используют газ гелий, конденсация которого происходит при достаточно низких температурах.

Рис. 4.41.