Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect3-2.html

Механика сплошных сред

Вытекание жидкости через отверстие в сосуде.

Пусть жидкость, заполняющая сосуд, под действием силы тяжести вытекает из него через отверстие в боковой стенке, расположенное вблизи дна сосуда (рис. 3.6). В отверстие вставлена горизонтальная трубка с закругленной внутренней кромкой, направляющая вытекающую струю воды. Закругленная кромка обеспечивает полное заполнение трубки вытекающей жидкостью.

Рис. 3.6.

Разобьем текущую жидкость на трубки тока. Одна из таких трубок изображена на рисунке 3.6. Хотя мы и не знаем, как выглядят эти трубки, однако все они начинаются на свободной поверхности жидкости и заканчиваются на выходном торце сливной трубки. Если площадь отверстия трубки S значительно меньше площади свободной поверхности S₀, то при истечении жидкости ее опускающаяся с некоторой скоростью v₀ поверхность будет оставаться горизонтальной. Это означает. что константа, входящая в уравнение Бернулли (3.14), будет одинакова для всех трубок тока: ${\rm const} = \frac{\rho v_0^2}{2}+p_0+\rho gH.$ Здесь H - высота уровня жидкости в сосуде. Поэтому скорость истечения жидкости v определяется из уравнения

$\frac{\rho v^2}{2}+ p_0 = \frac{\rho v_0^2}{2}+p_0+\rho gH,$

(3.17)

где p₀ - атмосферное давление на свободной поверхности и у сливной трубки. Поскольку S $\ll$ S₀, то из условия несжимаемости (3.2) следует, что v₀ $\ll$ v. С учетом этого скорость истечения из (3.17) получается равной

$v=\sqrt{2gH}.$

(3.18)

Эта формула носит название формулы Торичелли, поскольку была получена Торичелли, жившем до Бернулли. Сразу бросается в глаза, что скорость истечения жидкости из сосуда такая же, как и при ее свободном падении с высоты H. В этом нет ничего удивительного, поскольку вязкостью мы пренебрегли, а работа сил атмосферного давления над трубкой тока равна нулю. Поэтому, как и при свободном падении тел в отсутствие сопротивления воздуха, при ращение кинетической энергии равно работе силы тяжести: $\frac{\rho v^2}{2} = \rho gH.$ Справедливость формулы Торичелли можно легко проверить, если на выходную трубку надеть кусок гибкого шланга и вытекающую струю воды направить вверх под небольшим наклоном к вертикали (рис. 3.7). Струя поднимется практически до уровня поверхности жидкости. Если же струю направить вертикально вверх, то взлетающие вверх частицы жидкости, взаимодействуя с падающими вниз частицами, не смогут подняться на высоту H.

Рис. 3.7.

Интересно отметить, что трубки тока жидкости расположены преимущественно ближе к стенке сосуда с отверстием, в то время как у противоположной (левой на рис. 3.8) стенки жидкость практически малоподвижна. Это означает, что на левую стенку действуют силы давления, которое легко посчитать, используя линейный закон нарастания гидростатического давления с глубиной, даваемой формулой (2.11). Расчет сил давления, действующих на правую стенку, требует гидродинамического решения задачи. Однако и без такого расчета ясно, что в трубке тока, примыкающей к правой стенке, давление на каждой глубине будет меньше соответствующего этой глубине гидростатического давления. Это означает, что равнодействующая сил давления, действующих на обе стенки, направлена в сторону, противоположную направлению истечения жидкости. Под действием этой силы, называемой также реактивной, сосуд, поставленный на колеса, может придти в движение. Величину этой силы легко посчитать с использованием формулы Торичелли. По 3-му закону Ньютона искомая реактивная сила равна по величине силе, с которой стенки сосуда действуют на воду, сообщая ее (по 2-му закону Ньютона) приращение импульса в направлении истечения. Поскольку масса, вытекающая через отверстие с сечением S равна $\rho v S$ , то изменение импульса в единицу времени составит величину $\rho v^2 S.$ Поэтому реактивная сила

$F=\rho v^2 S = 2\rho gHS.$

(3.19)

Рис. 3.8.

Отметим, что если бы мы ошибочно приняли, что распределение давлений с глубиной у правой стенки было такое же, как у левой, то реактивная сила получилась бы вдвое меньшей:

$F'=\rho gH\cdot S,$

(3.20)

где $\rho gH$ - величина гидростатического давления на глубине H, S - площадь отверстия в правой стенке. Однако можно добиться одинакового (гидростатического) распределения давлений у обеих стенок, если конец трубки с острой кромкой будет отстоять от правой стенки, как показано на рис. 3.9. В этом случае реактивная сила может определяться с помощью формулы (3.20). Если же ее вычислять при помощи (3.19), то в этой формуле надо вместо сечения трубки S подставить сечение струи воды в трубке S_B=kS, где коэффициент истечения k $\approx$ 1/2. При таком истечении трубка будет заполнена жидкостью приблизительно наполовину.

Рис. 3.9.

Реактивную силу можно увеличить, если прежде всего повысить скорость истечения жидкости. Для этого следует использовать замкнутый сосуд с отверстием, при этом над свободной поверхностью жидкости создается давление p₁>p₀. Тогда скорость истечения жидкости из уравнения Бернулли получается равной:

$v=\sqrt{2\left( gH + \frac{p_1-p_0}{\rho}\right)},$

(3.21)

а реактивная сила возрастает линейно с повышением избыточного давления $\Delta p= p_1 - p_0$ над свободной поверхностью жидкости.

Гидрорезание.

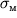
Если создать очень высокое избыточное давление, например, $\Delta \rho \approx$ 5000 атм = 5*10 Н/м2, то скорость истечения воды v = 1000 м/с. Если такую струю направить на какой-либо твердый материал, то его поверхность будет подвержена гидродинамическому давлению $$p_д=\rho v^2/2$=5000 атм.$ Такое огромное давление в ряде случаев может превосходить предел прочности $\sigma_м$ некоторых материалов, и последние будут разрушаться под действием струи. Со второй половины 80-х годов получило развитие новое направление в обработке материалов - гидрорезание. В этой технологии водяной нож - высоко-скоростная струя воды с диаметром иглы - легко режет материалы толщиной в несколько сантиметров со скоростью резания несколько десятков сантиметров в минуту. Для резки металлов, твердых сплавов, бетона и других материалов в струю добавляют абразивный порошок. Это позволяет значительно увеличить гидродинамическое давление и повысить производительность и возможности гидрорезания.

Сосуд Мариотта.

Весьма поучительным для понимания движения жидкости является истечение жидкости из сосуда Мариотта. Он позволяет обеспечить постоянную скорость вытекания жидкости из сосуда, несмотря на понижения ее уровня. Для этого в сосуд через герметичную пробку в его горловину вводится трубочка, сообщающаяся с атмосферой (рис. 3.10). Скорость вытекания определяется по формуле Торичелли $v=\sqrt{2gh}$ , где h - высота нижнего конца трубки над отверстием. Это происходит потому, что при незначительном истечении жидкости из полностью заполненного сосуда давление под пробкой будет меньше атмосферного, а давление в горизонтальной плоскости, совпадающей и нижним концом трубки, равно атмосферному. Скорость вытекания легко регулируется вертикальным перемещением трубки. Если конец трубки находится на уровне h=0 или ниже отверстия, то жидкость не вытекает вовсе.

Рис. 3.10.

Условие несжимаемости движущейся жидкости.

Равенство (3.2), являющееся условием несжимаемости, связывает скорости движущейся жидкости в двух различных сечениях. Между тем, как на это неоднократно обращалось внимание в предыдущих лекциях, в физике важно оперировать с равенствами или уравнениями, отнесенными к одной точке пространства. Для этого рассмотрим деформацию движущегося кубического элемента жидкости. Если его объем через малый отрезок времени $\delta t$ не изменяется, то сумма диагональных элементов тензора деформации равна нулю, т.е. $\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}=0$ Здесь u_x, u_y и u_z- смещения граней кубика в направлении соответствующих осей координат. Однако эти смещения связаны со скоростями движения граней (а точнее, частиц жидкости, находящихся в данный момент на этих гранях): $u_x=v_x \delta t, u_y=v_y \delta t, u_z=v_z \delta t.$ Подставляя эти равенства в (3.22), получаем локальное (относящееся к одной точке пространства) условие несжимаемости в виде

$\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}=0$

(3.22)

В физике для описания векторных полей, а в нашем случае речь идет о векторном поле скоростей v=v(x,y,z,t), используется понятие дивергенции (истока) поля в данной точке пространства. В декартовой системе координат выражение для div v имеет вид:

${\rm div }\; {\bf v} = \frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}$

(3.23)

Дивергенция вектора является скалярной функцией координат и времени и легко рассчитывается, если известны компоненты векторного поля (в нашем случае v_x, v_y и v_z). Поэтому условие (3.22) постоянства объема несжимаемой жидкости записывается кратко:

${\rm div }\; {\bf v} = 0.$

(3.24)

Отметим, что уравнение (3.24) является одним из основных уравнений гидродинамики несжимаемой жидкости. Следует отметить, что имеется множество векторных полей, как, например, электрическое E=E(x,y,z,t) и магнитное B=B(x,y,z,t) поля и др., при описании которых также широко используется понятие дивергенции: div E или div B и т.д. Хотя она определяется в соответствии с (3.23), вводится, однако, несколько из других соображений, поскольку в электродинамике не идет речь о движении и деформации элемента материальной среды. На примере векторного поля скоростей v=v(x,y,z,t) поясним фундаментальный смысл понятия дивергенции. Для этого рассмотрим неподвижный элементарный объем пространства. dV=dxdydx и посчитаем объем жидкости, втекающий и вытекающий из этого объема за единицу времени. Введем понятие элементарного потока вектора скорости v через маленькую площадку dS:

$dN_v = v\cdot dS\cdot \cos\alpha = vdS,$

(3.25)

где dS=ndS - вектор, направленный по нормали n к элементарной площадке. Ясно, что поток (3.25) равен объему жидкости, пересекающей площадку dS за единицу времени (рис. 3.12). Он допускает также наглядную геометрическую интерпретацию. В самом деле, в соответствии с определением линий тока, данным в начале этой лекции, их густота характеризует скорость течения. Поэтому величине скорости всегда можно поставить в соответствие количество линий тока, пересекающих площадку с dS=1 и n || v. Тогда поток dN_v в (3.25) будет характеризоваться числом линий, пересекающих площадку при ее произвольной ориентации.

Рис. 3.12.

Теперь легко посчитать баланс между втекающей и вытекающей жидкостью для элементарного объема, изображенного на рис. 3.12. Для этого восстановим внешние нормали по всем 6-ти граням кубика и посчитаем потоки жидкости через его грани. Легко понять, что положительное значение потока будет для вытекающей жидкости, а отрицательное - для втекающей. Если скорость в центре кубика v(x,y,z) изменяется при приближении к соответствующим граням, то при вычислении такого потока это необходимо учесть. Результирующий поток определится следующим образом:

$dN_v =\left[v_x\left(x + \frac{dx}{2}, y,z,t\right) - v_x\left(x - \frac{dx}{2},y,z,t\right)\right]dydz + \left[v_y\left(x,y + \frac{dy}{2},z,t\right) - v_y\left(x,y - \frac{dy}{2},z,t\right)\right]dxdz + \left[v_z\left(x,y,z + \frac{dz}{2},t\right) - v_z\left(x,y,z - \frac{dz}{2},t\right)\right]dxdy.$

(3.26)

Разделив левую и правую части (3.26) на dxdydz и переходя к пределу, получаем

$\frac{dN_v}{dxdydz} = {\rm div }\; {\bf v}$

(3.27)

Таким образом, дивергенция вектора скорости численно равна потоку жидкости через поверхность единичного объема. Если жидкость несжимаема, то, естественно, этот поток должен быть равен нулю. Графически последнее интерпретируется как равенство количества входящих и выходящих линий тока для этого объема. Это, в свою очередь, означает, что в окрестности точки, где div v=0, линии тока не прерываются. Поэтому равенство div v=0 называют условием неразрывности. Из школьного курса физики известно, что силовые линии электростатического поля (аналог линий тока) прерываются только на зарядах. Поэтому для областей, не занятых зарядами, мы также вправе написать ${\rm div }\; {\bf v} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y}\frac{\partial E_z}{\partial z} = 0$ . Силовые линии индукции магнитного поля B всегда замкнуты, поэтому во всех случаях div B=0.

Назад | Вперед