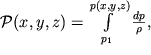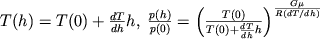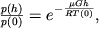Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect2-3.html

Механика сплошных сред

Равновесие сжимаемой жидкости.

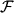
При внутренних напряжениях плотность газов не остается постоянной. Можно считать, что давление является функцией плотности ( $p=p(\rho)$ ), причем вид этой функции, как будет показано ниже, задается условиями, при которых находится газ. Поэтому в механике сплошных сред в этих случаях оперируют с плотностью силы ${\cal F}$ , то есть с силой, приложенной к единице массы, которая связана с силой F в (2.7) соотношением

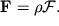
${\bf F}=\rho {\cal F}.$

(2.21)

Тогда условие равновесия (2.7) примет вид

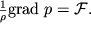
$\frac{1}{\rho}{\rm grad}\; p={\cal F}.$

(2.22)

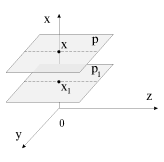
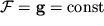
В левую часть этого равенства входят давление и плотность, являющиеся неизвестными функциями координат, а правая часть обычно известна. В поле силы тяжести ${\cal F}={\bf g}={\bf {\rm const}}$ . В этом случае поверхностями равных давлений и плотностей будут горизонтальные плоскости, две из которых p(x₁) = p₁ и p(x) = p изображены на рис. 2.15. Если мы введем вспомогательную функцию

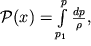
${\cal P}(x)=\int\limits_{p_1}^{p}\frac{dp}{\rho},$

(2.23)

то (2.22) может быть переписано в виде, аналогичном (2.7):

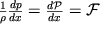
$\frac{1}{\rho}\frac{dp}{dx}=\frac{d{\cal P}}{dx}={\cal F}$

(2.24)

Вводя далее для единицы массы потенциальную энергию U₁, с которой внешняя сила связана соотношением

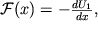
${\cal F}(x)=-\frac{dU_1}{dx},$

(2.25)

получаем уравнение, аналогичное (2.9):

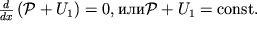
$\frac{d}{dx}\left( {\cal P} + U_1 \right) =0, или {\cal P} +U_1 = {\rm const}.$

(2.26)

Рис. 2.15.

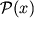
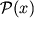
Замечание. Вспомогательная функция ${\cal P}(x)$ зависит от верхнего предела p интеграла (2.23), вычисление которого возможно при известной связи между давлением и плотностью. С другой стороны, если найти зависимость ${\cal P}(x)$ (с помощью (2.24) или (2.26)), то можно определить функцию p(x) в (2.23), что позволяет получить распределение давлений. 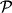Очевидно, что поверхности равного значения величины ${\cal P}$ совпадают с поверхностями равного давления. В задачах с трехмерным распределением давления и плотности вспомогательная функция

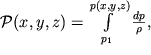
${\cal P}(x,y,z)=\int\limits_{p_1}^{p(x,y,z)}\frac{dp}{\rho},$

(2.27)

а условие равновесия имеет вид

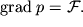
${\rm grad}\; p={\cal F}.$

(2.28)

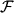
Поскольку сила ${\cal F}$ связана с потенциальной энергией единицы массы соотношением

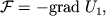
${\cal F}=-{\rm grad}\; U_1,$

(2.29)

то подстановка (2.29) в (2.28) дает условие

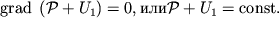
${\rm grad}\; \left( {\cal P} + U_1\right) =0, или {\cal P} + U_1={\rm const}.$

(2.30)

Следует отметить, что условие равновесия (2.28) является более общим, чем (2.7), т.к. позволяет рассчитать распределение давлений как в жидкостях, так и в газах.

Атмосфера в поле силы тяжести.

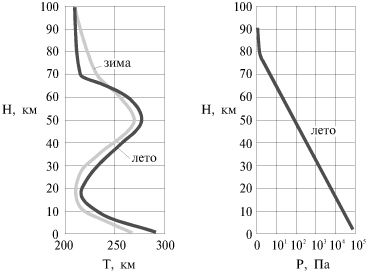
Многочисленные исследования атмосферы, проведенные при помощи аэростатов (см. ниже), ракет и искусственных спутников Земли, показывают, что по мере увеличения высоты давление и плотность монотонно убывают, а температура монотонно убывает лишь в нижнем 10-километровом слое, а в более высоких слоях меняется немонотонно. Параметры атмосферы зависят как от географического положения места, так и от времени года. В качестве иллюстрации к сказанному на рис. 2.16 представлены высотные зависимости параметров среднестатистической атмосферы Москвы, полученные в летнее и зимнее время. Если разница в высотных зависимостях температуры атмосферы составляет десятки градусов, то распределение "зимнего" давления отличается от "летнего" всего лишь на несколько процентов, и на рисунке эта разница неразличима. Сложная высотная зависимость температуры атмосферы есть результат совместного проявления процессов тепломассопереноса, инициируемых излучением Солнца. Расчеты показывают, что если бы атмосфера и Мировой океан, называемые жидкой оболочкой Земли, не поглощали бы энергию солнечного излучения, то Земля нагрелась бы на экваторе до 270 К, на Южном полюсе - до 150 К и на Северном полюсе - до 170 К. При таких температурах установилось бы радиационное равновесие: нагретая Земля излучала бы в мировое пространство столько энергии, сколько получает от Солнца. Однако поверхность Земли значительно теплее, а контраст температур между экватором и полюсом намного меньше. Это - результат поглощения солнечной энергии самой атмосферой. Кроме того, атмосфера и океан переносят тепло от одной области к другой, что также влияет на энергетический баланс. Поглощение солнечной энергии осуществляется главным образом водяным паром, углекислым газом и озоном, вследствие чего создается "парниковый эффект", приводящий к дополнительному нагреванию поверхности Земли. Поскольку воздух вблизи поверхности более теплый и легкий, чем воздух сверху, то он всплывает вверх (вертикальная конвекция), и нижний слой атмосферы перемешивается. Поэтому распределение температуры, изображенное на рис. 2.16, является результатом динамического равновесия атмосферы в поле силы тяжести, при котором соблюдается баланс энергии. Радиационное равновесие можно рассчитать, если принять во внимание, что в нижнем слое атмосферы основным физическим фактором, отвечающим за достижение равновесия, является поглощение радиации водяным паром. На больших высотах доминирующим является поглощение углекислым газом и озоном.

Рис. 2.16.

Атмосфера делится на отдельные участки, как это видно из рис. 2.16. Нижний слой атмосферы, называемый тропосферой, содержит 80% массы атмосферы, почти весь водяной пар и облака и характеризуется сильным вертикальным перемешиванием. Сверху тропосфера ограничена тропопаузой, где температура атмосферы меняется очень мало. Выше расположена стратосфера, которая слабо перемешивается. Ее устойчивость обусловливается повышением температуры с высотой в результате радиационного баланса. Возрастание температуры заканчивается в стратопаузе. Выше находится мезосфера, где температура опять падает. Мезосфера содержит лишь 0,1% массы всей атмосферы. Выше мезосферы (H>100 км) находится термосфера, в которой температура опять растет с высотой, достигая 600 К в период спокойного Солнца и более 2000 К в период солнечной активности. Для вычисления изменения атмосферного давления с высотой воспользуемся условием равновесия (2.24) в виде:

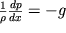
$\frac{1}{\rho}\frac{dp}{dx}=-g$

(2.31)

Связь между давлением и плотностью для сухого воздуха задается уравнением состояния идеального газа

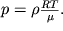
$p=\rho \frac{RT}{\mu}.$

(2.31)

Справедливость использования этого уравнения обусловлена тем, что влияние влажности на плотность воздуха существенно лишь в тропиках вблизи поверхности Земли, однако даже здесь ошибка при использовании (2.32) не превосходит 2%. Подставляя значение плотности $\rho$ из (2.32) в (2.31), получаем уравнение

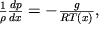
$\frac{1}{\rho}\frac{dp}{dx}=-\frac{g}{RT(x)},$

(2.33)

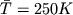
которое можно проинтегрировать, если известна T(x). В качестве грубого приближения в (2.33) можно использовать среднее значение температуры ${\bar T} = 250 K$ , при этом отклонение максимальной температуры у поверхности или минимальной температуры на высоте H = 100 км от среднего значения составляют около 15%. Интегрируя (2.33), получаем распределение давления изотермической атмосферы

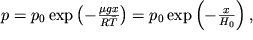
$p=p_0\exp\left(-\frac{\mu gx}{R{\bar T}}\right)=p_0\exp\left(-\frac{x}{H_0}\right),$

(2.34)

носящее название барометрической формулы. Высота H₀, на которой давление падает в e раз, называется приведенной высотой атмосферы и равна:

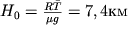
$H_0 = \frac{R{\bar T}}{\mu g} = 7,4 км$

(2.35)

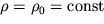
Отметим, что если бы плотность не менялась с высотой ( $\rho = \rho_0 ={\rm const}$ ), то интегрирование (2.31) привело бы к линейному (как для несжимаемой жидкости) закону убывания давления с высотой:

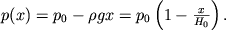
$p(x)=p_0-\rho gx=p_0\left(1-\frac{x}{H_0}\right).$

(2.36)

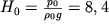
В этом случае вся атмосфера была бы ограничена высотой $H_0=\frac{p_0}{\rho_0 g}=8,4$ км, что, конечно, противоречит реальной ситуации. Для практических целей используются унифицированные атмосферные параметры и их высотные зависимости. Так, Международная организация гражданской авиации (МОГА) для нужд авиации определила в 1952 г. стандартную атмосферу до высоты 20 км, а в 1963 г. дала новое определение до высоты 32 км. Стандартная атмосфера есть условная атмосфера, для которой давление и температура на уровне моря, градиент температуры и другие значения были выбраны намеренно так, чтобы получить схематичную модель атмосферы, которая наилучшим образом согласуется со средними значениями ее параметров, наблюдаемыми на средних широтах. Эта модель, в частности, широко используется для градуирования альтиметров (приборов для определения высоты летательного аппарата). В этой модели принимается, что до высоты h = 11000 стандартных геопотенциальных метров над уровнем моря, где температура воздуха равна -56,5 ${}^\circ$ С, градиент температуры dT/dh равен -0,0065 ${}^\circ$ С на стандартный геопотенциальный метр. До высоты 20000 стандартных геопотенциальных метров dT/dh=0, а выше, вплоть до 32000 стандартных геопотенциальных метров, градиент температуры равен +0,001 ${}^\circ$ С на стандартный геопотенциальный метр. Геопотенциальный метр является единицей измерения геопотенциала, определяемого уравнением

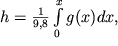
$h=\frac{1}{9,8}\int\limits_{0}^{x}g(x)dx,$

(2.37)

где ускорение свободного падения

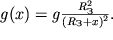
$g(x)=g\frac{R_З^2}{(R_З + x)^2}.$

(2.38)

Здесь R_З - радиус Земли, g - ускорение свободного падения на среднем уровне моря, x - высота над уровнем моря. Если бы ускорение g не менялось с высотой, то высота h в геопотенциальных метрах была бы равна геометрической высоте над уровнем моря x. В модели стандартной атмосферы соотношения между давлением p, температурой Т, плотностью $\rho$ и геопотенциалом h задаются следующим образом:

В двух атмосферных слоях с постоянным градиентом температур
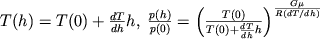
$T(h)=T(0)+\frac{dT}{dh}h,\; \frac{p(h)}{p(0)}=\left(\frac{T(0)}{T(0) + \frac{dT}{dh}h}\right)^{\frac{G\mu}{R(dT/dh)}}$ (2.39)
В изотермическом атмосферном слое, где dT/dh = 0 и T(0) = const,
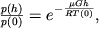
$\frac{p(h)}{p(0)}=e^{-\frac{\mu Gh}{RT(0)}},$ (2.40)

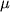
и работает барометрическая формула. Здесь p(0) и T(0) - давление и температура у основания каждого слоя, R - универсальная газовая постоянная для сухого воздуха, h - разница геопотенциала между рассматриваемой точкой слоя и его основанием, $\mu$ - молекулярная масса сухого воздуха, коэффициент G = 9,80665, если геопотенциал выражен в геопотенциальных метрах. Учет изменения температуры с высотой приводит к высотной зависимости давления (2.39), которая является лучшей аппроксимацией реальной атмосферы, чем барометрическая формула. Для более глубокого ознакомления с использованием модели стандартной атмосферы для практических целей воздухоплавания и др. рекомендуем читателю обратиться к международным метеорологическим таблицам.

Назад | Вперед