Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect2-1.html

Механика сплошных сред

Лекция 2

Жидкость и газ в состоянии равновесия. Условия равновесия. Распределение давлений в жидкости, находящейся во внешнем поле. Плавание тел. Распределение плотности и давления в атмосфере. Воздухоплавание. Центрифугирование. Под действием внешних сил в жидкости и газах, как и в твердых телах, могут возникать внутренние напряжения. Рассматривая их как сплошные среды, мы отметим, что жидкости, не имея определенной формы, сохраняют практически неизменным свой объем. Газы же не имеют ни определенной формы, ни фиксированного объема. В жидкости (далее этот термин будет использоваться и для газов, за исключением только отдельно оговариваемых случаев) силы сцепления между молекулами малы, и жидкость не оказывает сопротивления растяжению Однако при сжатии силы отталкивания между молекулами могут быть весьма значительными. По этой причине говорят не о растягивающих напряжениях $\sigma_{ij}$ , а о давлениях $p_{ij} = - \sigma_{ij}$ , как об отрицательных (сжимающих) напряжениях. Совокупность давлений p_ij, действующих на площадки, ограничивающие элемент жидкости, называется тензором давлений. Опыт показывает, что в покоящейся или медленно движущейся жидкости тангенциальные давления p_ij (i\ne j), связанные с вязкостью жидкости, отсутствуют. В этом можно убедиться, заставив, например, массивное тело, плавающее на поверхности жидкости, перемещаться вдоль поверхности под действием сколь угодно малой силы. В этой ситуации касательные напряжения, передаваемые от верхнего (увлекаемого телом) слоя к нижним слоям жидкости, пренебрежимо малы.

Закон Паскаля.

Если пренебречь вначале силами тяготения, действующими на каждую частицу жидкости (или силами инерции, если таковые существуют), то из простейших соображений относительно условий равновесия элемента жидкости следует, что

p₁₁ = p₂₂ = p₃₃ = p,

(2.1)

при этом давление p, являющееся скалярной величиной, одинаково во всех точках объема, занятого покоящейся жидкостью. Условие (2.1) автоматически обеспечивает не только равенство нулю суммы сил давления, приложенных к данному элементу, но равенство нулю суммарного момента этих сил. Для его доказательства рассмотрим неподвижную жидкость, помещенную в цилиндрический сосуд сечением S₁, закрытый сверху поршнем (рис. 2.1, левый сосуд). Если надавить на поршень с силой F₁, то в жидкости будут созданы внутренние напряжения (давления). На единицу поверхности элемента жидкости будет действовать сжимающая сила f_ii = - p_iin_i, направленное противоположно внешней нормали n_i к i-ой поверхности (на рис. 2.1 изображены только две силы).

Рис. 2.1.

Поскольку силы, действующие на противоположные грани кубика, равны по величине, то p₁₁=F₁/S₁. Равенство давлений p₁₁ и р₂₂ следует из условия равновесия половины кубика, выделенного более темным цветом и изображенного на фрагменте. Действительно, f₁₁=f₂₂=f/ $\sqrt{2}$ , поэтому р₂₂=р₁₁. Рассматривая равновесие элементарных объемов в различных точках жидкости, получим условие:

$p_{ii} = p = \frac{F_1}{S_1},$

(2.2)

которое и является математическим выражением закона Паскаля. Если этот сосуд соединить при помощи трубки с другим цилиндрическим сосудом сечением S₂, то при открывании крана K внутренние напряжения по жидкости, находящейся в соединительной трубке, в соответствии с законом Паскаля передадутся во второй сосуд (рис. 2.1). На поршень, его закрывающий, жидкость будет давить вверх с силой

$F_2 = pS_2 = \frac{F_1}{S_1}S_2.$

(2.3)

Если S₂>S₁, то развиваемое усилие F₂>F₁. Этот выигрыш в силе используется во многих гидроприводящих устройствах (гидроприводах): в приводе ковша экскаватора, рулей ракет и самолетов. На этом же принципе работает гидравлический пресс, гидравлический домкрат и т.д. В системе СИ за единицу давления принимается Паскаль (Па), при этом 1Па=1Н/1м². В технике в качестве единицы давления используется техническая атмосфера: 1ат=1кГс/1см²=9,8*10⁴ Па.

Жидкость во внешнем поле.

Рассмотрим напряжения, возникающие в жидкости, находящейся в поле тяжести или в поле сил инерции, когда сосуд с жидкостью может двигаться с ускорением. Пусть к кубическому элементу жидкости объемом dV=dxdydz приложена внешняя сила FdV (F - сила, приложенная к единице объема жидкости, (рис. 2.2). В результате возникающих внутренних напряжений на нижнюю грань кубика с координатой x и площадью dy*dz в положительном направлении оси x действует сила давления величиной p(x,y,z)dydz, а на верхнюю грань - p(x+dx,y,z)dydz. При равновесии кубика, очевидно, необходимо, чтобы

Рис. 2.2.

p(x,y,z)dydz - p(x+dx,y,z)dydz + F_xdxdydz = 0

(2.4а)

Аналогичные по смыслу равенства должны быть записаны и по двум оставшимся осям координат:

p(x,y,z)dxdz - p(x,y+dy,z)dxdz + F_ydxdydz = 0

(2.4б)

p(x,y,z)dxdy - p(x,y,z+dz)dxdy + F_zdxdydz = 0

(2.4в)

Разделив левые и правые части записанных выше равенств на объем элемента, получаем условия равновесия в виде дифференциальных уравнений

$- \frac{\partial p}{\partial x} + F_x = 0; - \frac{\partial p}{\partial y} + F_y = 0; - \frac{\partial p}{\partial z} + F_z = 0.$

(2.5)

Уравнения (2.5) показывают, что давление не остается постоянным и изменяется в тех направлениях, по которым действует внешняя сила. Если ввести вектор градиента давления

${\rm grad} p = \nabla p = \frac{\partial p}{\partial x}e_x + \frac{\partial p}{\partial y}e_y + \frac{\partial p}{\partial z}e_z,$

(2.6)

где e_x, e_y и e_z - единичные векторы вдоль осей координат, то уравнения (2.5) запишутся в более компактном векторном виде

-grad p + F = 0

(2.7)

В соответствии со смыслом введенного в предыдущих лекциях вектора градиента скалярной величины из (2.7) следует, что давление наиболее быстро нарастает в направлении действия внешней силы F, а в перпендикулярных направлениях остается постоянным. Таким образом, можно говорить о поверхностях равного давления, нормаль к которым в каждой точке совпадает с направлением приложенной в этой точке внешней силы. Несложно рассчитать распределение давлений по объему жидкости, если принять во внимание, что компоненты внешней силы F выражаются через производные пока неизвестной скалярной функции координат p(x,y,z). Это означает, что сила F должна быть потенциальной и, следовательно, может быть выражена через потенциальную функцию U (потенциальную энергию единицы объема жидкости во внешнем поле) следующим образом:

F = -grad U

(2.8)

Подставив (2.8) в (2.7), получим

grad (p + U) = 0, или p + U = const.

(2.7)

Константа в (2.9) определяется из условия нормировки потенциала и давления.

Жидкость в поле силы тяжести.

Пусть несжимаемая жидкость (например, вода) находится в поле тяжести $F = \rho g$ , при этом $\rho = {\rm const}$ . Для расчета распределения давлений удобно направить ось x вдоль силы тяжести, совместив ее начало со свободной поверхностью жидкости. Поскольку потенциальную функцию можно записать в виде $U(x) = -\rho gx$ (нормировка потенциала такова, что U(0)=0), то распределение давлений по глубине определяется из соотношения

$p(x) - \rho gx = {\rm const}$

(2.10)

Константа C определяется из условия равенства давления на поверхности воды атмосферному давлению p₀. Следовательно,

$p(x) = p_0 + \rho gx.$

(2.11)

Если принять атмосферное давление $p_0 \approx 10^5$ Па, плотность воды $\rho = 10^3$ кг/м³, то из (2.11) легко посчитать, что с увеличением глубины на каждые 10 метров ( $\Delta x$ =10 м) давление увеличивается на величину атмосферного давления ( $\Delta p = p_0$ ). Важно отметить, что возрастание давления с глубиной не зависит от формы сосуда, в который налита жидкость. Яркой иллюстрацией справедливости этого утверждения является одинаковость уровней жидкости в двух сообщающихся сосудах произвольной формы (рис. 2.3). Действительно, равенство двух горизонтальных сил давления, обеспечивающих равновесие кубика жидкости в нижней части сообщающихся сосудов возможно лишь при равенстве высот столбов воды в обоих сосудах.

Рис. 2.3.

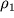
Проиллюстрируем несколько экспериментов с сообщающимися сосудами. Пусть оба колена U-образного сосуда (рис. 2.4) разделены подвижной перегородкой П, при этом правое колено заполнено водой, а левое - ртутью, плотность которой $\rho_1$ более чем в 10 раз превышает плотность воды $\rho$ ( $\rho_1 = 13,6\rho$ ). Очевидно, равновесие в этой ситуации достигается при высоте столба ртути $h_1 = \frac{\rho}{\rho_1}h$ , значительно меньшей высоты столба воды h. Уместно помнить, что столб ртути высотой h₁=760 мм уравновешивает давление 10-метрового столба воды, или почти 10-километрового столба атмосферы. Поэтому для измерения атмосферного давления используют ртутные манометры, а атмосферное давление измеряют в миллиметрах ртутного столба. Такой манометр представляет собой два сообщающихся сосуда, заполненных ртутью. Один из сосудов в виде тонкой трубки заполнен сверху и из него удален воздух, а второй сообщается с атмосферой (рис. 2.5).

Рис. 2.4.

Рис. 2.5.

Если измеряемые давления на 1-2 порядка меньше атмосферного давления, то можно использовать и водяные манометры (см. Последующие лекции). Завершая описание равновесия жидкости, отметим, что в Мировом океане из-за больших глубин формула (2.11) нуждается в уточнении, т.к. плотность увеличивается с глубиной. За исключением нескольких необычных мест она может меняться от географического положения в пределах 2% от постоянной величины $\rho$ = 1035 кг/м3. Обычно колебания плотности обусловлены колебаниями температуры и солености воды.

Назад | Вперед