Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect1-2.html

Механика сплошных сред

Упругие тела

Как уже отмечалось выше, при деформациях возникают внутренние напряжения, силы которых, в общем случае, зависят не только от деформаций, но и от скоростей, с которыми эти деформации происходят. В этом легко убедиться, если взять полимерное вещество, которое при обычных условиях медленно растекается подобно замазке, принимая форму сосуда, в котором оно находится. Можно без особых усилий изменить его форму, если делать это медленно. Однако, если вылепить шарик, то легко обнаружить, что такой шарик обладает хорошими упругими свойствами, подскакивая практически после удара об пол на ту же высоту, с которой он был брошен без начальной скорости. Этот опыт показывает, что силы деформации, подобно силам вязкого трения, возрастают по мере увеличения скорости деформации. В ряде практически важных случаев силы напряжения определяются только деформациями. Такие тела, в которых это имеет место, называются абсолютно упругими телами, или упругими телами. Замечательным свойством таких тел является способность полностью восстанавливать свою форму после снятия внешних усилий, прикладываемых к телу. Рассмотрим, например, растяжение (или сжатие) стержня (рис. 1.1) с силой F, приложенной перпендикулярно к торцевой грани с площадью сечения S. Опыт показывает, что при последовательном возрастании нагрузки вначале деформации развиваются равномерно по длине стержня и растут пропорционально нагрузке, т.е.

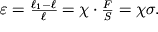
$\varepsilon = \frac{\ell_1 - \ell}{\ell} = \chi \cdot \frac{F}{S} = \chi\sigma.$

(1.18)

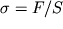
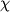
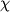
Величина $\sigma= F/S$ называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций $\varepsilon$ соответствующим напряжениям выражает закон Гука. Коэффициент пропорциональности $\chi$ называется коэффициентом удлинения и для каждого материала определяется опытным путем. Так как численные значения $\varepsilon$ гораздо меньше $\varepsilon$ , то $\chi$ - весьма малая величина. 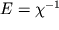Поэтому обычно вводят модуль упругости (модуль Юнга) $E=\chi^{-1}$ , и закон Гука окончательно записывают в виде

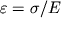
$\varepsilon = \sigma / E$

(1.19)

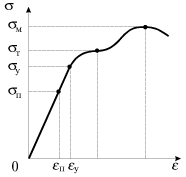
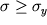
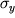
Опыт показывает, что этот закон выполняется лишь в определенном интервале напряжений. Если растягивать стержень, последовательно увеличивая от нуля возрастающую силу, то каждый раз, после снятия нагрузки, деформация исчезает. Однако при некотором напряжении $\sigma \ge \sigma_y$ появляется заметное остаточное удлинение. Это напряжение $\sigma_y$ называется пределом упругости. На рис. (1.7) изображена зависимость деформаций от напряжений, называемая диаграммой растяжений. 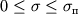Следует отметить, что закон Гука выполняется только в части области упругости - области пропорциональности, когда $0\le\sigma\le\sigma_{п}$ .

Рис. 1.7.

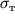
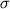
При возрастании нагрузки наблюдается явление текучести, т.е. внезапный рост удлинения образца при постоянной нагрузке $\sigma_т$ , называемой пределом текучести. Отметим, что течение материала происходит равномерно по всей длине стержня. За пределами области текучести дальнейшее удлинение стержня сопровождаетсяувеличением $\sigma$ . Однако деформации будут распределены уже неодинаково по дине стержня (рис. 1.8.) - в некотором месте можно заметить образование шейки. 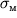При напряжении $\sigma_м$ , называемом пределом прочности, в этом ослабленном сечении происходит разрыв.

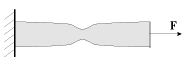Рис. 1.8.

То напряжение, которое данный материал может выдержать на практике, не разрушаясь и не получая опасной деформации, называют допустимым и обозначают $[\sigma]$ . Обычно $[\sigma]<\sigma_п$ , и все расчеты проводят на основе законов Гука. Чтобы обеспечить прочность при всех обстоятельствах допустимое напряжение выбирается как часть предела прочности, в частности, для металлов $[\sigma]=0.2 \sigma_м$ , а для дерева $[\sigma]=0.1 \sigma_м$ . Следует отметить, что наибольшие деформации, которые может выдержать материал, не определяются протяженностью области текучести. Если область текучести велика, то материал называется пластичным. Такой материал, как, например, сталь, способен выдерживать большие нагрузки без разрушения. Наоборот, если область текучести невелика, то этот материал хрупок. 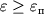Хрупкие материалы, как чугун, например, разрушаются при деформациях $\varepsilon\ge\varepsilon_п$ . 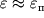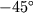Однако в ряде случаев пластичные материалы могут разрушаться и при малых деформациях $\varepsilon\approx\varepsilon_п$ (например, сталь при температуре ниже $-45^{\circ}$ С). Аналогичными свойствами обладают и сдвиговые деформации. В частности, в области пропорциональности связь между деформациями сдвига и касательным напряжением (рис. 1.2) задается соотношением

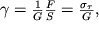
$\gamma = \frac{1}{G}\frac{F}{S}=\frac{\sigma_\tau}{G},$

(1.20)

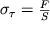
в котором $\sigma_\tau=\frac{F}{S}$ - касательное напряжение, аналогичное по смыслу введенному выше нормальному напряжению, а G - модуль сдвига, являющийся, как и модуль Юнга, также характеристикой материала.

Материал	Модуль упругости E	Модуль сдвига G	Предел пропорциональности 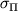$\sigma_П$	Предел текучести 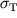$\sigma_Т$	Предел прочности при растяжении 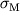$\sigma_М$
Сварочная сталь	2000	770	1,3...1,6	1,8...2,6	3,3...4,0
Пружинная сталь незакаленная	2200	850	5,0 и выше	-	до 10 и выше
Пружинная сталь закаленная	2200	850	8,5 и выше	-	до 17
Медь	1100...1300	415...440	-	0,7	22
Серый чугун	750...1050	290...400	-	-	1,2...2,4
Свинец	140...180	55...80	-	0,05	0,14...0,18

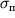
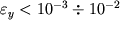
В таблице приведены характеристики упругости и прочности некоторых материалов. Из этой таблицы можно сделать два важных вывода. Во-первых, поскольку предел пропорциональности $\sigma_п$ на 2-3 порядка меньше модуля упругости, то в области упругости деформации $\varepsilon_y<10^{-3}\div 10^{-2}$ .

Рис. 1.9.

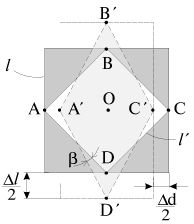
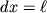
Во-вторых, просматривается связь между величиной модуля Юнга E и модуля сдвига G - чем больше E, тем больше и G. Это не случайно, т.к. между обеими величинами существует жесткая связь. Чтобы ее установить, рассмотрим растяжение маленького кубика с длиной стороны $dx=\ell$ , как это было изображено на рис. 1.9. Обратим внимание, однако, на то, что квадратная грань ABCD параллелепипеда, находящегося внутри рассматриваемого кубика, превращается при деформациях в ромбическую грань A'B'C'D'. Совершенно ясно, что параллелепипед испытывает сдвиговую деформацию, а его объем при этом практически не изменился (см. также формулу (1.17)). 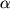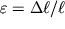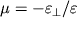Величину угла сдвига $\alpha$ можно легко связать с деформацией удлинения $\varepsilon=\Delta \ell / \ell$ и коэффициентом Пуассона $\mu=-\varepsilon_\perp / \varepsilon$ . Из треугольника A'OD' следует, что

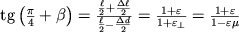
${\rm tg}\left( \frac{\pi}{4}+\beta \right) = \frac{\frac{\ell}{2}+\frac{\Delta\ell}{2}}{\frac{\ell}{2}-\frac{\Delta d}{2}} = \frac{1+\varepsilon}{1+\varepsilon_\perp}=\frac{1+\varepsilon}{1-\varepsilon\mu}$

(1.21)

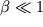
Поскольку $\beta\ll 1$ , то

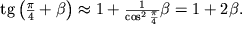
${\rm tg}\left( \frac{\pi}{4}+\beta \right) \approx 1 + \frac{1}{\cos^2\frac{\pi}{4}}\beta = 1 + 2 \beta.$

(1.22)

Приравнивая правые части (1.21) и (1.22), находим

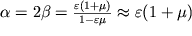
$\alpha=2\beta=\frac{\varepsilon(1+\mu)}{1-\varepsilon\mu} \approx \varepsilon(1+\mu)$

(1.23)

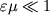
В последней формуле учтено, что $\varepsilon\mu\ll 1$ .

Рис. 1.10.

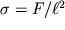
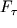
Сила F, растягивающая кубик (рис. 1.10), создает нормальное напряжение $\sigma=F/\ell^2$ . Это напряжение передается на грани AB и BC параллелепипеда, однако силы, действующие на каждую из его граней, имеют не только нормальную к грани, но и направленную вдоль грани параллельную составляющую $F_\tau$ . Касательное напряжение оказывается при этом равным

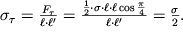
$\sigma_\tau=\frac{F_\tau}{\ell\cdot\ell'}=\frac{\frac{1}{2}\cdot\sigma\cdot\ell\cdot\ell\cos\frac{\pi}{4}}{\ell\cdot\ell'}=\frac{\sigma}{2}.$

(1.24)

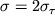
Поскольку деформации $\varepsilon$ в формуле (1.23) пропорциональны напряжениям, a $\sigma=2\sigma_\tau$ , то

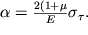
$\alpha = \frac{2 (1+\mu}{E}\sigma_\tau.$

(1.25)

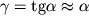
Сравнивая последнее равенство с соотношением (1.20) при учете, что $\gamma={\rm tg}\alpha\approx\alpha$ , находим искомую связь между модулями Юнга и сдвига:

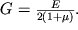
$G=\frac{E}{2(1+\mu)}.$

(1.26)

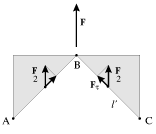
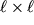
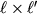
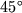
В рассмотренном примере следует обратить внимание на то, что величина и направление силы, приложенной к некоторой площадке, зависит от ориентации и величины этой площадки. Так, на грань $\ell\times\ell$ куба действует сила F, перпендикулярная к грани, в то время как на грань параллелепипеда $\ell\times\ell'$ действует сила F/2, направленная под углом $45^\circ$ к этой грани. Этот частный вывод получит далее обобщение при обсуждении способов задания сил, действующих на каждый из элементов тела. Посмотрим, что будет происходить с тем же кубиком, если его растягивать одновременно силами, приложенными ко всем его граням. В этом случае относительные удлинения каждой из его сторон будет задаваться соотношениями:

$\varepsilon_1=\frac{\sigma_1}{E}-\frac{\varepsilon_2}{\mu^{-1}}-\frac{\varepsilon_3}{\mu^{-1}}=\frac{\sigma_1-(\sigma_2 + \sigma_3)\mu}{E},$

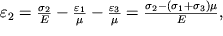$\varepsilon_2=\frac{\sigma_2}{E}-\frac{\varepsilon_1}{\mu}-\frac{\varepsilon_3}{\mu}=\frac{\sigma_2-(\sigma_1 + \sigma_3) \mu}{E},$

(1.27)

$\varepsilon_3=\frac{\sigma_3}{E}-\frac{\varepsilon_2}{\mu}-\frac{\varepsilon_3}{\mu}=\frac{\sigma_3-(\sigma_1 + \sigma_2) \mu}{E}.$

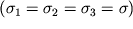
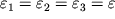
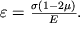
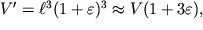
Формулы (1.27) описывают деформации кубика при его всестороннем растяжении или сжатии. Если напряжения одинаковы $(\sigma_1=\sigma_2=\sigma_3=\sigma)$ , то деформации также будут одинаковы: $\varepsilon_1=\varepsilon_2=\varepsilon_3=\varepsilon$ , и $\varepsilon=\frac{\sigma(1-2 \mu)}{E}.$ В результате всесторонней деформации новый объем кубика станет равным $V'=\ell^3(1+\varepsilon)^3 \approx V(1+3\varepsilon),$ а его относительное изменение составит величину

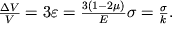
$\frac{\Delta V}{V} = 3\varepsilon = \frac{3(1-2\mu)}{E}\sigma=\frac{\sigma}{k}.$

(1.28)

Параметр

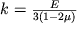
$k = \frac{E}{3(1-2\mu)}$

(1.28)

называется модулем всестороннего сжатия и играет важную роль в теории упругости. Важно отметить, что хрупкие материалы, подвергнутые всестороннему давлению, на которое дополнительно накладывается растяжение, сжатие или сдвиг, обнаруживают значительные пластические деформации. Такие деформации играют существенную роль, например, в процессах образования рельефа земной коры: граниты и базальты, хрупкие в обычных условиях, текут под действием колоссального давления в глубинных слоях Земли. Деформации растяжения и сдвига возникают в практически важных случаях изгибов балок строительных конструкций и окруживания валов машин и механизмов.

Назад | Вперед