Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect1-1.html

Механика сплошных сред

Лекция 1

Деформации твердого тела. Понятие о тензоре деформации. Абсолютно упругое тело и его деформации. Упругие напряжения. Модули Юнга, сдвига и коэффициент Пуассона. Деформации при изгибе и кручении, устойчивость тел при деформациях. Энергия упругих деформаций. В лекциях по механике твердого тела мы предполагали, что под действием приложенных сил в теле, хотя и происходят деформации, тем не менее мы не принимали их в расчет для описания движения этого тела как целого. Во многих важных случаях учет деформаций является определяющим, например, когда речь идет о целой области физики - о механике сплошной среды или о расчете прочности многочисленных конструкций и деталей машин и механизмов, базирующемся на отдельной инженерной науке, называемой сопротивление материалов и т.д. Вначале мы рассмотрим поведение твердых тел, которые деформируются под действием приложенных сил. Надо отметить, что основное положение механики деформируемых твердых тел, рассматриваемых как сплошные среды, были разработаны в начале XIX в. И составляют основу современной теории упругости. Опыт показывает, что под действием приложенных сил тела в той или иной степени меняют свою форму и объем, что на микроскопическом уровне означает относительное смещение атомов, составляющих тело. Для удобства описания деформаций мысленно разобьем тело на физически малые объемы (иногда их будем называть частицы), содержащие, однако, большое число атомов. В отсутствие деформаций атомы находятся в состоянии теплового равновесия, а все малые объемы - в механическом равновесии. Тогда сумма сил, действующих на выделенный объем со стороны примыкающих к нему других объемов будет равна нулю. Смена расположения атомов при деформациях приводит к тому, что в теле возникают внутренние силы, или внутреннее напряжение, стремящиеся вернуть тело в состояние равновесия. Важно отметить, что внутренние силы, как силы молекулярного взаимодействия, являются короткодействующими. Только соседние атомы или молекулы эффективно взаимодействуют друг с другом. Это упрощает ситуацию, поскольку позволяет считать, что силы, действующие на малый объем, приложены к ограничивающей его поверхности.

Элементарные деформации. Коэффициент Пуассона.

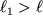
При всем многообразии случаев произвольную деформацию тела можно свести к двум элементарным деформациям - растяжению (сжатию) и сдвигу. Обратимся к опыту. Закрепим один конец резинового шнура длиной $\ell$ и потянем за другой конец с постоянной силой. Шнур придет в новое положение равновесия с длиной $\ell_1 > \ell$ (рис. 1.1). Такую простейшую деформацию можно охарактеризовать относительным удлинением

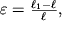$\varepsilon = \frac{\ell_1 - \ell}{\ell},$

(1.1)

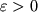
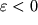
При этом растяжение соответствует $\varepsilon > 0$ , а сжатию - $\varepsilon < 0$ .

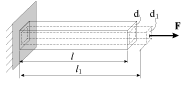Рис. 1.1.

Деформацию сдвига можно наблюдать в опыте с резиновым кубиком, если закрепить, например, его нижнее основание, а к верхнему основанию приложить касательную силу. (рис. 1.2)Деформация в этом случае будет характеризоваться параметром

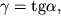$\gamma = {\rm tg} \alpha,$

(1.2)

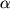
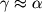
зависящим от угла сдвига $\alpha$ , который в большинстве практически важных случаев мал, и $\gamma \approx \alpha$ .

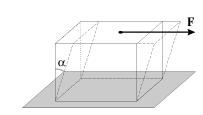Рис. 1.2.

Отметим также известный факт, что при растяжении резинового шнура его поперечный размер d уменьшается до величины d₁. Такое поперечное сжатие характеризуется параметром

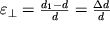$\varepsilon_\perp=\frac{d_1 -d}{d}=\frac{\Delta d}{d}$

(1.3)

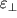
Опытным путем установлено, что отношение $\varepsilon_{\perp}$ к $\varepsilon$ приблизительно одинаково для разных деформаций одного и того же материала. В теории упругости материал характеризуется коэффициентом Пуассона

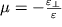$\mu =-\frac{\varepsilon_\perp}{\varepsilon}$

(1.4)

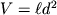
Каково численное значение коэффициента Пуассона? Чтобы ответить на этот вопрос, посчитаем изменение объема резинового шнура. В отсутствие деформации его объем $V = \ell d^2$ , объем же деформированного шнура

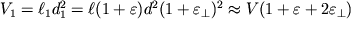$V_1=\ell_1 d^2_1=\ell (1+\varepsilon)d^2(1+\varepsilon_\perp)^2\approx V(1+\varepsilon +2\varepsilon_\perp)$

(1.5)

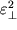
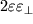
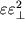
В последнем выражении мы пренебрегли малыми величинами $\varepsilon_\perp^2$ , $2\varepsilon\varepsilon_\perp$ и $\varepsilon\varepsilon_\perp^2$ . С учетом (1.4) относительное изменение объема запишется в виде

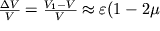$\frac{\Delta V}{V} = \frac{V_1 - V}{V} \approx \varepsilon (1 - 2\mu$

(1.6)

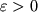
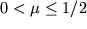
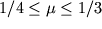
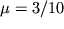
Поскольку при растяжении ( $\varepsilon > 0$ ) объем никогда не уменьшается, то $0 < \mu \le 1/2$ . Для изотропных материалов, имеющих одинаковые механические свойства по всем направлениям, коэффициент Пуассона $1/4 \le \mu \le 1/3$ , в частности, для металлов $\mu = 3/10$ .

Понятие о тензоре деформации

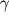
В рассмотренных выше случаях мы имели дело с одномерными однородными деформациями растяжения и сдвига (вдоль одного направления), где $\varepsilon$ и $\gamma$ оказывались одними и теми же для всех элементарных объемов резинового шнура. Во многих случаях ситуация гораздо сложнее: с одной стороны, деформации меняются от точки к точке (неоднородные деформации), а с другой стороны не являются одномерными. 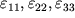Последнее означает, что деформации в некоторой точке P описываются тремя деформациями растяжения $\varepsilon_{11}, \varepsilon_{22}, \varepsilon_{33}$ маленького кубика с т. P внутри (рис. 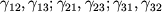1.3) и двумя сдвигами каждой из трех граней кубика: $\gamma_{12}, \gamma_{13}; \gamma_{21}, \gamma_{23}; \gamma_{31}, \gamma_{32}$ . Здесь первый индекс i означает, что грань кубика перпендикулярна оси X_i, второй индекс j означает, что грань смещается вдоль оси X_j. Таким образом, неоднородные деформации в каждой точке тела в общем случае характеризуются набором 9 величин деформаций, являющихся функциями координат. Эти девять величин составляют тензор деформаций, однако независимы лишь 6 его величин.

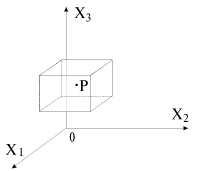Рис. 1.3.

Рассмотрим несколько подробнее подход, используемый для описания деформации в некоторой точке P, приводящий к введению понятия тензор деформаций. Пусть тело находится к недеформированном состоянии, и известно положение каждой из его частиц, задаваемых радиус-вектором r относительно некоторой системы координат как, например, положение т. P на рис 1.4. При деформировании все его точки, вообще говоря, смещаются. Смещение каждой точки можно охарактеризовать вектором смещения u(x₁, x₂, x₃), являющегося при неоднородных деформациях функцией координат. Однако деформации в точке будут определены лишь тогда, если известно смещение соседних с т. P частиц тела. Таким образом, задание смещения всех частиц тела полностью определяет его деформацию. В самом деле, рассмотрим две бесконечно близкие точки P(x₁, x₂, x₃) и P'(x₁+dx₁,x₂+dx₂,x₃+dx₃), имеющие смещения u(x₁,x₂,x₃) и u'=u(x₁+dx₁,x₂+dx₂,x₃+dx₃). 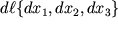Из рисунка нетрудно видеть, что если взаимное расположение точек в недеформированном состоянии задавалось радиус-вектором $d\ell\{dx_1,dx_2,dx_3\}$ проекции , то в результате деформаций новое взаимное расположение задается вектором

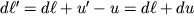$d\ell'=d\ell+u' -u=d\ell+du$

(1.7)

В частности, если u'=u, то деформации в т. P отсутствуют.

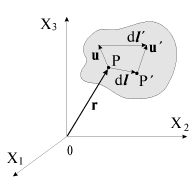Рис. 1.4.

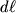
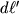
Для удобства описания деформаций возведем (1.7) в квадрат и будем оперировать модулями векторов $d\ell$ и $d\ell'$ .Тогда

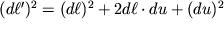$(d\ell')^2=(d\ell)^2+2d\ell\cdot du +(du)^2$

(1.8)

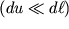
В равенстве (1.8) пренебрежем последним членом в правой части, поскольку снижаем деформации малыми $(du\ll d\ell)$ , а проекции вектора du представим в виде сумм

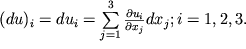$(du)_i=du_i=\sum\limits_{j=1}^3\frac{\partial u_i}{\partial x_j}dx_j; i=1,2,3.$

(1.9)

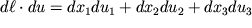
Выражение (1.9), по существу описывает приращение каждой из трех проекций вектора смещения при переходе из т.P в т.P', и содержит три слагаемых, каждое из которых есть произведение производной функции u_i в т.P на приращение соответствующего аргумента dx_j. Расписывая в (1.8) скалярное произведение в виде $d\ell\cdot du=dx_1 du_1+dx_2 du_2+dx_3 du_3$ и подставляя (1.9) в (1.8), получим

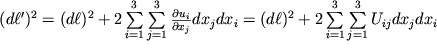$(d\ell')^2=(d\ell)^2+2\sum\limits_{i=1}^3\sum\limits_{j=1}^3 \frac{\partial u_i}{\partial x_j}dx_j dx_i=(d\ell)^2+2\sum\limits_{i=1}^3\sum\limits_{j=1}^3 U_{ij} dx_j dx_i$

(1.10)

где, по определению,

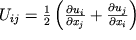$U_{ij}=\frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right)$

(1.11)

- тензор деформаций. Из его определения видно, что он является симметричным тензором (U_ij= U_ji). Для описания деформаций в каждой т.P можно выбрать такую систему координат, в которой только три диагональные компоненты тензора U₁₁, U₂₂ и U₃₃ отличны от нуля. Как и в случае приведения тензора инерции к главным осям, уместно напомнить, что для каждой точки тела P существуют свои три главные оси, относительно которых формула (1.10) имеет наиболее простой вид:

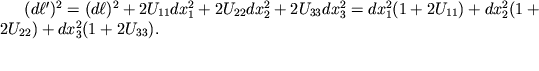$(d\ell')^2=(d\ell)^2 + 2U_{11}dx_1^2+ 2U_{22}dx_2^2 + 2U_{33}dx_3^2 = dx_1^2 (1+2U_{11}) + dx_2^2 (1+2U_{22}) + dx_3^2 (1+2U_{33}).$

(1.12)

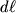
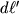
В качестве примера рассмотрим деформацию сдвига в резиновом кубе, изображенном на рис. 1.2. Для удобства нанесем на его боковую грань прямоугольную сетку, разбивающую эту грань на маленькие квадратики со сторонами, параллельными ее диагоналям (рис. 1.5а). При деформации квадратики превращаются в прямоугольники (рис. 1.5б). Если под $d\ell$ и $d\ell'$ понимать длины диагоналей элементарных квадратика и прямоугольника соответственно, то эти длины можно связать формулой (1.12) только в системе координат, оси которой X₁ и Х₂ направлены вдоль ребер элементарных ячеек (ось Х₃ перпендикулярна плоскости чертежа).

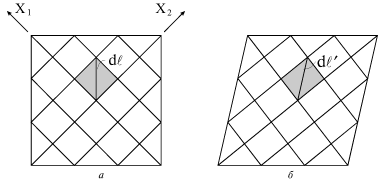Рис. 1.5.

Обобщая полученный результат, следует сказать, что при произвольных деформациях главные оси в любой точке Р должны быть направлены параллельно ребрам элементарного прямоугольного параллепипеда, который при деформации остается прямоугольным параллепипедом. Деформации сдвига относительно главных осей координат отсутствуют. Ниже мы установим связь между деформациями сдвига и недиагональными компонентами тензора деформаций. Выясним далее физический смысл диагональных компонент U₁₁, U₂₂ и U₃₃. Относительное удлинение каждой из граней призмы равно соответствующей диагональной компоненте тензора деформаций. В самом деле

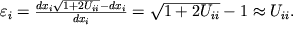$\varepsilon_i=\frac{dx_i \sqrt{1+2U_{ii}}-dx_i}{dx_i}=\sqrt{1+2U_{ii}}-1\approx U_{ii}.$

(1.13)

Пусть в окрестности т. P(x₁,x₂,x₃) деформации таковы, что кубик со сторонами dx₁, dx₂ и dx₃ превращается в параллелепипед.Для наглядности рассмотрим кратину деформации в плоскости X₁ X₂. Смещения вершин квадрата при деформации изображены соответствующими векторами. Длины прямоугольника в направлении главных осей X₁ и X₂ изменились до величин

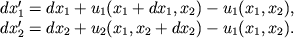$\begin{array}{l} dx'_1=dx_1 + u_1(x_1+dx_1,x_2)-u_1(x_1,x_2),\\ dx'_2=dx_2 + u_2(x_1,x_2+dx_2)-u_1(x_1,x_2). \end{array}$

(1.14)

Из (1.14) легко вычисляются относительные удлинения:

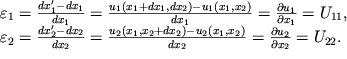$\begin{array}{l} \varepsilon_1=\frac{dx'_1-dx_1}{dx_1}=\frac{u_1(x_1+dx_1,dx_2)-u_1(x_1,x_2)}{dx_1}=\frac{\partial u_1}{\partial x_1}=U_{11},\\ \varepsilon_2=\frac{dx'_2-dx_2}{dx_2}=\frac{u_2(x_1,x_2+dx_2)-u_2(x_1,x_2)}{dx_2}=\frac{\partial u_2}{\partial x_2}=U_{22}. \end{array}$

(1.15)

С использованием соотношения (1.13) легко также связать изменение элементарного объема с диагональными компонентами тензора. Объем элементарного параллелепипеда

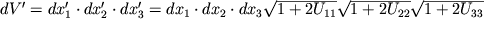
$dV'=dx'_1\cdot dx'_2 \cdot dx'_3 = dx_1\cdot dx_2 \cdot dx_3 \sqrt{1+2U_{11}}\sqrt{1+2U_{22}}\sqrt{1+2U_{33}}$

(1.16)

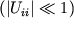
и также изменяется при деформациях. Относительное изменение этого объема при малых деформациях $(|U_{ii}|\ll 1)$ , как следует из (1.16), равно:

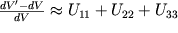
$\frac{dV'-dV}{dV}\approx U_{11}+U_{22}+U_{33}$

(1.17)

Важно отметить, что при сдвиге объем тела не меняется. Поэтому при деформациях сдвига сумма диагональных компонент тензора деформаций (иногда употребляют термин "след тензора"), приведенного к главным осям, равна нулю (см. ниже).

Рис. 1.6.

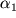
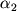
Поясним далее физический смысл недиагональных компонент тензора деформации. Пусть параллелепипед испытывает деформацию, в результате которой прямоугольник на рис. 1.6 превращается в параллелограмм. В рассматриваемом примере мы отвлекаемся, как и ранее, от смещения частиц вдоль оси X₃. Легко далее посчитать углы $\alpha_1$ и $\alpha_2$ , на которые повернулись стороны параллелограмма относительно сторон параллелепипеда. 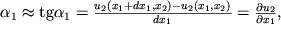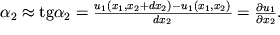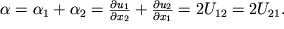Они, очевидно, равны $\alpha_1\approx {\rm tg} \alpha_1 = \frac{u_2(x_1+dx_1,x_2)-u_2(x_1,x_2)}{dx_1}=\frac{\partial u_2}{\partial x_1},$ $\alpha_2\approx {\rm tg} \alpha_2 = \frac{u_1(x_1,x_2+dx_2)-u_1(x_1,x_2)}{dx_2}=\frac{\partial u_1}{\partial x_2}.$ Тогда угол сдвига $\alpha=\alpha_1 + \alpha_2 = \frac{\partial u_1}{\partial x_2} + \frac{\partial u_2}{\partial x_1} = 2 U_{12} = 2 U_{21}.$ Таким образом, недиагональные компоненты тензора деформаций определяет сдвиговые углы $\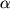alpha$ в соответствующих плоскостях.

Назад | Вперед