Астронет > Карта движений планет

Астронет: Е.И. Ковязин Место, содержание и методика преподавания вопросов движения небесных светил в курсе астрономии средней школы
http://variable-stars.ru/db/msg/1173487/chapter8.html

Методика преподавания движения небесных светил

<< Предыдущая

Содержание

Следующая >>

§ 2. Карта движений планет и методика работы с ней.

Впервые такое обобщенное пособие было предложено А.Д. Могилко (А.Д. Марленским - [179]). Описанная им "Карта движения планет" была предназначена для иллюстрации видимых и действительных движений планет солнечной системы.

В дальнейшем совместная работа автора с А.Д. Марленским привела к окончательному оформлению этого пособия, разработке системы упражнений, решаемых с его помощью, и к изданию его.

Предлагаемое нами пособие, полное описание которого предлагается ниже, мы назвали "Карта движений планет"¹ (см. приложение).

Карта иллюстрирует вопросы не только видимых или действительных движений планет, комет, астероидов и других естественных тел солнечной системы, но и позволяет наглядно раскрыть смысл связей между ними. Это осуществляется на примерах действительно происходящих движений этих тел.

Оказалось очень удобным использование Карты для изучения движений и искусственных тел солнечной системы (АМС, космические корабли, зонды и т. д.), так как их движения происходят по тем же законам классической механики (этим занимается небесная механика), что и движения естественный спутников нашего Солнца. Сам факт использования одного пособия для решения задач по движению как естественных, так и искусственных тел солнечной системы способствует более глубокому пониманию школьником универсальности закономерностей классической механики. Это является важным шагом на пути формирования диалектико-материалистического мировоззрения школьника.

Кроме того, сам характер выбранного нами выполнения данного пособия позволяет решить многие задачи практической астрономии, связанные с переходом от планетоцентрических координат любой из планет к гелиоцентрическим.

Таким образом, "Карта движений планет" является пособием, служащим для изучения истинных и связанных с ними видимых движений планет, для преобразования планетоцентрических (геоцентрических, ареоцентрических и т.д.) координат в гелиоцентрические и наоборот, а также может быть использована при приближенных нахождения орбит автоматических межпланетных станций, посылаемых к планетам солнечной системы.

Не трудно видеть, что по своим возможностям "Карта движений планет" значительно выходит за рамки школьного курса астрономии. Однако её использование на уроках астрономии при изучении целого ряда вопросов, связанных с движениями тел солнечной системы, оказывается очень удобным и оправданным, более подробно это будет показано ниже.

В наш век начавшегося покорения космического пространства и находящихся в нем тел, вопросы движений небесных тел, как естественных, так и искусственных интересуют не только школьников, но и большие круги людей различных специальностей.

В литературе отсутствуют пособия, позволяющие в наглядной форме и в то же время с достаточной точностью изучать вопросы небесной механики и космонавтики. Обычно движения небесных тел, рассматриваемые в курсах небесной механики, представлены в сложной математической форме, трудно доступной для понимания читателями, не владеющими соответствующим математическим аппаратом. Поэтому не все читатели могут познакомиться с теорией движения небесных тел и научиться решать задачи, связанные с полетами к планетам солнечней системы.

Предлагаемая "Карта движений планет" является пособием для первоначального ознакомления с трудными вопросами небесной механики и космонавтики. Она позволяет приближенно решать некоторые задачи по космонавтике с удовлетворительной для ознакомительных целей точностью, причем для их решения вполне достаточно математической подготовки в объеме курса элементарной математики в средней школе.

Поэтому данная Карта может широко применяться не только на занятиях по астрономии и космонавтике в высшей и средней школах, но и может быть использована любителями этих предметов на занятиях астрономических кружков, в планетариях и т. д.

Достоинством Карты является то, что она позволяет в наглядной форме одновременно показать действительные движения небесных тел по орбитам их движений вокруг Солнца и их видимые перемещения в проекции на пояс зодиакальных созвездий.

При этом видимые движения любого тела солнечной системы могут быть определены с какой- угодно планеты, а так же с любого положения автоматической межпланетной станции при всевозможных полетах.

Описание карты.

"Карта движений планет" расположена (см. приложение) на двух листах. На основном листе в центре Карты представлено Солнце, вокруг которого изображены орбиты первых четырех планет: Меркурия, Венеры, Земли, Марса и кольцо зодиакальных созвездий. На втором листе показаны орбиты следующих четырех планет: Юпитера, Сатурна, Урана, Нептуна и дана линия эклиптики. Орбита планеты Плутон не обозначена, т.к. эта планета является очень трудной для наблюдений.

В кольце зодиакальных созвездий тонкими сплошными синими линиями нанесена сетка экваториальных координат. Линии сетки проведены через 1 час по прямым восхождениям и через 15 градусов по склонениям. По внутреннему краю пояса зодиакальных созвездий проставлены цифры 0, 1, 2, ... 23, показывающие значения прямых восхождений в часах. На кругах склонений, проходящих через 0, 6, 12, 18 часов обозначены величины склонений. Общая ширина пояса зодиакальных созвездий около 47 градусов. Жирная синяя линия, проходящая эксцентрично по поясу зодиакальных созвездий - линия небесного экватора.

Эклиптика обозначена жирной красной линией. Она разбита на градусы от 0 до 360 градусов. Градусные деления представляют собой гелиоцентрические долготы, отсчитываемые от точки весеннего равноденствия.

На поясе зодиакальных созвездий тонкими пунктирными красными линиями показаны границы созвездий, а характер конфигураций ярких звезд в созвездиях выделен тонкими синими линиями.

Орбиты всех планет обозначены тонкими сплошными черными линиями, а рядом с орбитами проведены пунктирные линии, показывающие в масштабе карты гелиоцентрические широты планет - отклонения планет от плоскости эклиптики, если смотреть на планеты из центра Солнца.

Внешняя часть пунктира по отношению к орбите обозначает отклонение в северные широты от эклиптики, а внутренняя - в южные.

На орбите Земли проставлены календарные даты года, показывающие соответствующие положения Земли на её орбите. Так как гелиоцентрические долготы Земли для одних и тех же календарных дат из года в год колеблются незначительно (в масштабе карты этими колебаниями можно пренебречь), то можно считать, что в одинаковые календарные даты разных лет гелиоцентрические долготы Земли будут иметь одно и то же значение.

Гелиоцентрические долготы Меркурия, Венеры, Марса приведены на десять лет вперед (1970-1980 гг.) с интервалом в 20 суток в таблицах NN 12 - 22 приложения к диссертации.

На орбитах Юпитера, Сатурна, Урана и Нептуна проставлены даты, показывающие, когда планеты находятся в отмеченных точках своей орбиты.

В области зодиакальных созвездий на карте нанесены все звезды до 5,75 видимой звездной величины включительно, т. е. все звезды, видимые при хороших условиях наблюдения невооруженным глазом. Звезды обозначены черными кружками, размер которых зависит от блеска звезды, с градацией через 0,5 зв. величины. При этом

к 1-й зв. вел. относятся звезды от 0,76 до 1,25 зв. вел.
к 1,5 зв. вел. относятся звезды от 1,26 до 1,75 зв. вел.
к 2-й зв. вел. относятся звезды от 1,76 до 2,25 зв. вел.
.................
к 5,5 зв. вел. относятся звезды от 5,26 до 5,75 зв. вел.

На карте обозначено несколько шаровых и рассеянных звездных скоплений, суммарная звездная величина которых меньше или равна 6,0. Такие скопления могут быть видны невооруженным глазом при хороших условиях наблюдения.

На карту нанесены также некоторые двойные звезды, в основном такие, двойственность которых может быть обнаружена или невооруженным глазом, или с помощью бинокля с небольшим увеличением. Угловое расстояние между ними колеблется в пределах от 40" до 1300". В "Звездном атласе"² профессора А.А. Михайлова такие звезды названы "близкими" звездами.

Для более удобной работы карту следует наклеить на толстый лист картона и обрезать по окружности. Чтобы центральное отверстие не разнашивалось, в центре карты нужно укрепить металлическую пластину с отверстием. Гвоздем (его диаметр должен точно соответствовать диаметру отверстия) карта крепится к оклеенной бумагой стене так, чтобы она могла вращаться вокруг оси. Дополнительно к карте изготавливаются два набора фишек планет и фишка Солнца (см. рис. 9), насажанные на короткие и тонкие шпильки. Фишки можно сделать из отфиксированной и окрашенной фотопленки. Фишки одного набора проставляются на орбитах планет, другого набора - на фоне зодиакальных созвездий.

Рис. 9

Если карту наклеить на тонкий лист железа, а фишки на маленькие магнитики, то работа с картой будет более удобной.

Использование "Карты движений планет".

Рассмотрим ряд типовых задач, которые позволяет решать "Карта движений планет".

1. Преобразование гелиоцентрических экваториальных координат светил (звезд, планет, АМС) - a, d в гелиоцентрические эклиптические координаты – l, b и наоборот.

На "Карте движений планет", фактически нанесены две сетки координат: сетка гелиоцентрических экваториальных координат (тонкие синие линии) и равномерная концентрическая сетка эклиптических координат, причем на карте представлена лишь её основа - линия эклиптики. Поэтому "Карта движений планет" позволяет легко решать задачи, связанные с преобразованием данных координат. Пусть нам нужно определить гелиоцентрические эклиптические координаты точки, имеющей экваториальные гелиоцентрические координаты a = 14^ч47^м и d = -15⁰,7 (a Весов). Находим данную точку на поясе зодиакальных созвездий. Соединим её прямой линией с центром Солнца. Точка пересечения данной прямой с эклиптикой даст нам значение гелиоцентрической эклиптической долготы - l - 224⁰,4 . Так как нам известен масштаб карты, то, измеряя расстояние от построенной точки до эклиптики, определим значение гелиоцентрической эклиптической широты b = +0⁰,6.

Аналогичным образом решается и обратная задача.

Решение задач на преобразование гелиоцентрических экваториальных координат в эклиптические и, наоборот, с помощью "Карты движений планет" возможно для гелиоцентрических координат только звезд (но не планет, или других тел солнечной системы).

2. Нахождение положения планеты на её орбите по известной гелиоцентрической долготе.

Положение Юпитера, Урана, Сатурна и Нептуна проставлены на орбитах их движений на несколько лет вперед (для Юпитера на период с 1970 по 1981 гг.; для Сатурна - 1970-1999 гг.; Урана - 1970-2035 гг.; Нептуна - 1970-2045 гг. с интервалами в 1 месяц для Юпитера и 3 месяца для остальных). Поэтому определение положения вышеперечисленных планет на их орбитах сводится к отысканию отметок соответствующих дат, а при их отсутствии - к линейной интерполяции - т.е. отысканию положения планеты на орбите по известным двум положениям на ближайшие даты.

Для нахождения положения Венеры, Земли и Марса на орбитах их движений необходимо взять значение гелиоцентрической долготы планеты в интересующую нас дату из таблицы, рассчитанной на нужный год (таблицы NN 12 - 22 приложения к диссертации). При отсутствии значения долготы планеты в данную дату определяем её значение по двум соседним датам методом линейной интерполяции. Гелиоцентрические долготы Меркурия можно взять из "Астрономического календаря" на соответствующий год.

Затем, отмечаем на эклиптике точку с полученной гелиоцентрической долготой и соединяем её с центром Солнца. Планета будет находиться в точке пересечения данной прямой с орбитой планеты.

3. Определение гелиоцентрических эклиптических координат планет по известным положениям планет на их орбитах.

Для того, чтобы определить значение гелиоцентрической долготы планеты по известному положению планеты на её орбите, нужно провести прямую линию через центр Солнца и центр фишки, отмечающей положение планеты. Пересечение этой прямой с эклиптикой даст значение гелиоцентрической эклиптической долготы планеты.

Для определения гелиоцентрической широты планеты измеряем расстояние вдоль проведенной прямой между орбитой планеты и пунктирной линией, проведенной рядом с ней. Зная масштаб карты, выражаем значение гелиоцентрической широты в градусах.

4. Определение видимого положения Солнца на фоне зодиакальных созвездий для наблюдателя, находящегося на любой планете солнечной системы.

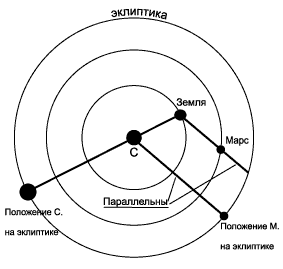Рис. 10. Определение видимого положения Солнца и планеты для земного наблюдателя.

Чтобы найти проекцию Солнца на пояс зодиакальных созвездий для наблюдателя, находящегося, например, на Земле, нужно отметить фишкой положение Земли в интересующую вас дату. Если провести прямую, проходящую через центры фишек, обозначающих Землю и Солнце, то точка пересечения этой прямой с эклиптикой (см. рис. 10) даст нам видимое положение Солнца на эклиптике.

Аналогично решается подобная задача и для любой другой планеты солнечной системы. При этом нужно помнить, что Солнце будет проектироваться не на эклиптику, а выше или ниже её, в зависимости от гелиоцентрической широты планеты. Точное положение Солнца определяется путем откладывания от эклиптики в противоположную сторону гелиоцентрической широты планеты в масштабе карты. Например, 18 октября Солнце для земного наблюдателя будет находится в созвездии Девы вблизи a Девы - Спики. Для марсианского наблюдателя 26 октября 1971 года Солнце было видно также в созвездии Девы вблизи h Девы .

5. Определение видимых положений планет среди звезд по их гелиоцентрическим долготам для наблюдателей, находящихся на любых планетах солнечной системы.

а) Земной наблюдатель.

Отмечаем с помощью фишек положение Земли и планеты на их орбитах на избранную дату. Проводим прямую линию через центры фишек планеты и Земли (см. рис. 10). Находим пересечение эклиптики с той из параллельных линий, которая проходит через центр Солнца. Получим значение гелиоцентрической долготы планеты. Так как плоскости орбит планет образуют небольшие углы с плоскостью эклиптики, то полученное положение уже является приближенным решением поставленной задачи.

Рис. 11 К определению
геоцентрической широты планеты.

Для уточнения положения планеты среди звезд необходимо найти её гелиоцентрическую широту по известным гелиоцентрическим координатам, если (см. рис. 11) планета находится над плоскостью эклиптики на высоте H и видна из центра Солнца пол углом b (о величине склонения мы судим по расстоянию от пунктира до орбиты - гелиоцентрической широте, см. карту), то с Земли, находящейся на другом расстоянии, она, конечно, будет видна под другим углом - b , большим (b > b), если планета находится ближе к Земле, чем к Солнцу, и меньшим (b < b), если она ближе к Солнцу, чем к Земле. Поэтому величину отклонения (b) нужно умножить на отношение расстояний планеты от Солнца и от Земли:

M₁, M₂ - два положения Земли относительно Солнца. Величины LC, LM измеряются линейкой по карте.

б) Внеземной наблюдатель.

Совершенно аналогичным образом решаются такие задачи и для внеземного наблюдателя. Так как в настоящее время подобные задачи встречаются редко, то можно ограничиться определением только планетоцентрических долгот рассматриваемых светил, хотя "Карта движений планет" позволяет определить и их планетоцентрические широты.

6. Определение гелиоцентрических координат планет по их видимым положениям среди звезд зодиакального пояса для земного наблюдателя.

Зная видимые экваториальные координаты планеты a , d , можно определить её гелиоцентрические эклиптические координаты: гелиоцентрическую долготу - l и гелиоцентрическую широту b. Для этого по известным a , d строим положение планеты среди звезд зодиакального пояса. Полученную точку соединяем прямой линией с центром Солнца. Через центр фишки, отмечающей положение Земли (положение Земли должно быть отмечено в соответствующую дату), проводим прямую линию, параллельную проведенной выше. Планета будет находиться в точке пересечения её орбиты с данной прямой.

Отмечаем положение планеты фишкой. Определение гелиоцентрических координат планеты по известному действительному положению планеты на её орбите было описано выше (см. пункт 3).

7. Определение действительного положения автоматической межпланетной станции среди тел солнечной системы по её геоцентрическим экваториальным координатам.

Большой интерес представляет применение "Карты движений планет" для решения задач, связанных с движением автоматических межпланетных станций. Точное решение таких задач - чрезвычайно сложная математическая задача, решение которой под силу лишь специалистам. Однако приближенное решение таких задач с помощью "Карты движений планет" очень наглядно и несложно.

В сообщениях ТАСС о полетах автоматических межпланетных станций обычно указывается расстояние от этих станции до Земли и их видимые экваториальные координаты в определенный момент времени. На основании знания этих данных можно построить гелиоцентрическое положение АМС. Решение таких задач значительно упрощается тем, что орбиты АМС образуют небольшие углы с эклиптикой.

Для определения гелиоцентрической долготы АМС на поясе зодиакальных созвездий строим точку по известным a , d , указанным в сообщении. Полученная точка - видимое геоцентрическое положение АМС среди звезд. Соединяем данную точку с Солнцем прямой линией. Через центр фишки, обозначающей положение Земли на орбите в соответствующий момент времени, проводим прямую линию, параллельную проведенной выше. На этой линии в масштабе карты откладываем расстояние, на котором находилась АМС в момент времени, указанный и сообщении. Полученную точку отмечаем. В ней находится станция. Для более точного решения поставленной задачи необходимо найти её гелиоцентрическую широту. Если (см. рис.11) L - АМС, находящаяся над плоскостью на высоте H, то

Величины ML, CL измеряются линейкой по карте.

8. Определение элементов орбиты АМС и построение орбиты.

Описанное выше определение положения АМС позволяет определить её гелиоцентрические координаты:

l - гелиоцентрическую долготу,
b - гелиоцентрическую широту,
r - радиус-вектор.

Двух таких определений вполне достаточно для того, чтобы найти все шесть элементов орбиты АМС (см. Вентцель М.К. "Основы теоретической астрономии", М., 1962, стр. 109-116). Но поскольку в таком случае решение получается очень сложным, лучше построить ещё одну, третью точку. В этом случае задача может быть решена элементарными методами.

Рассмотрим определение элементов орбиты АМС на основании знания трех положений её.

Рис.12. К определению элементов
орбиты АМС.

Поскольку полеты к планетам солнечней системы проходят под небольшими углами к плоскости эклиптики, то для первоначального ознакомления с орбитой вполне достаточно ограничиться определением трех элементов орбиты: большой полуоси - a, эксцентриситета - l, долготы перигелия - p . Знание уже этих трех элементов орбиты АМС позволяет простым методом вычертить данную орбиту на карте. Пусть (см. рис. 12) точки - A, B, C - три известные положения в движении АМС по её орбите. Дуги AB, AC, BC являются разностями истинных аномалий станции, находящейся в точках A, B, C , т.е. угол ASB = a , а угол ASC = b . Тогда уравнения эллипса в полярных координатах для указанных трех точек запишутся так:

P = r₁ (1+l*cosV);

P = r₂ {1+ l*cos(V+a )};

P = r₃ {1+ l*cos(V+b )}

Неизвестными величинами будут p, l, V. Приравнивая первые два уравнения выразим l. Приравнивая второе и третье уравнения также выразим l . Из полученных двух уравнений после несложных преобразований найдем:

Величины r, r₂ ,r₃ измеряются линейкой по карте, а углы a и b являются разностями гелиоцентрических долгот станции. Определив таким образом истинную аномалию V, по вышенаписанным формулам найдем вначале l, а из первого начального уравнения - P. Далее находим большую полуось орбиты АМС:

Зная истинную аномалию и гелиоцентрическую долготу АМС в точке A, определяем долготу перигелия:

p = l_A - p

Рис. 13. Построение орбиты АМС.

По найденном значениям l, a, p легко построить орбиту АМС на "Карте движений планет". Для этого откладываем на эклиптике вычисленное значение гелиоцентрической долготы перигелия и через полученную точку и центр Солнца проводим прямую. Эта прямая показывает направление большой оси орбиты АМС. Один из фокусов орбиты - Солнце. Для того, чтобы найти второй фокус (см. рис. 13), нужно отложить от центра Солнца вдоль по большой оси дважды величину:

c = a * l

Полученная точка является вторым фокусом орбиты АМС. Зная два фокуса эллипса и величину его большой полуоси, можно вычертить его следующим простым способом. В точки фокусов втыкаются две булавки, соединенные петлей из нитки. Длина нитки равняется удвоенной большой полуоси эллипса. С помощью карандаша вычерчиваем орбиту АМС. Точки A, B, C должны лежать на данном эллипсе. Если этого не произойдет, то вычисления и построения нужно повторить и найти ошибку.

Пример:

Пусть нам известны видимые экваториальные координаты трех положений автоматической межпланетной станции на её орбите и моменты времени, в которые станция находилась в этих точках (координаты даны на 0 часов по всемирному времени):

Таблица № 9.

Дата	Прямое восхождение	Склонение	Расстояние от Земли до АМС
20 декабря	05^ч10^м	+ 22⁰,8	23 млн.км.
14 февраля	05^ч25^м	+ 23⁰,0	83 млн.км.
1 мая	08^м19^м	+ 20⁰,3	205 млн.км.

Для построения орбиты АМС строим сначала на поясе зодиакальных созвездий три видимых положения АМС по известным экваториальным координатам a и d. Построенные точки лежат на линии эклиптики, значит, движение АМС происходит в плоскости эклиптики. Проводим прямую линию через центр Солнца и одну из построенных точек. На параллельной линии, проходящей через центр фишки, обозначающем положение Земли на орбите в момент наблюдения, откладываем в масштабе карты расстояние, на котором находилась АМС в соответствующее время. В полученной точке находится станция (см. п. 7). Аналогично строим второе и третье положения АМС.

Измеряя линейкой, расстояние от центра Солнца до построенных точек, найдем величины радиус-векторов.

r₁ = 1.130 а.е. r₂ = 1.324 а.е. r₃ = 1.580 а.е.

Продолжая прямые, соединяющие центр Солнца с построенными точками до эклиптики, определим значения гелиоцентрических долгот станции, находящейся в указанных точках:

l₁ = 86⁰,8 l₂ = 123⁰,2 l₃ = 162⁰,4

Вычисляем разности истинных аномалий станции a и b как разности гелиоцентрических долгот:

a = 36⁰,4 b = 75⁰,6

Пользуясь ранее полученными формулами, находим:

tg V = 2.013 откуда V = 63⁰,6

Далее определяем:

l = 0,265
p = 1,359 а.е.
l_p = 23⁰,2

Таким образом, мы определили три основные элемента орбиты станции.

На основании этих данных строим на "Карте движений планет" орбиту АМС (см. рис.13). Полученное решение является достаточно точным и полным для случая движения АМС в плоскости эклиптики.

При движении АМС под небольшими углами к плоскости эклиптики (что и имеет место в случае межпланетных перелетов) подобное решение также дает достаточно точное представление о движении АМС, но не является полным.

Рис. 14 К определению i, W , T₀
орбиты АМС.

Для тех, кто заинтересуется более точным и полным решением данной задачи, нужно определить ещё три элемента орбиты станции i, W , T₀ . Определим вначале i. Орбита АМС пересекает небесную сферу по линии C, B, A, K под углом i к эклиптике (см. рис. 14).

Наметим на чертеже полюс эклиптики - P и полюс орбиты АМС - L и соединим их дугами больших кругов с точками A₁, C₁.

Тогда:

И C₁L = LA₁ = 90⁰;
И PC = 90⁰ - b₃;
И A₁B = 90⁰ - b₁;

Дуга PL равна углу наклона орбиты к эклиптике:

И PL = i; И PLC₁ = j ; И C₁LA = Y

Так как угол Y равен дуге AC , то его можно определить из соотношения:

cos Y = sin b₁ sinb₃ + cos b₁ cos b₃ cos (l₁-l₃)

В сферическом треугольнике C₁PL :

cos (90⁰-b₃) = sin i * cos j

Откуда:

В сферическом треугольнике PAL:

cos (90⁰-b₁)=sin i * cos( j + Y );

т.е. sin b₁ = sin i (cos j cos y –sin j sin y )

Подставив в это уравнение выше полученные значения cos j и sin j, после сокращений и преобразований окончательно найдем:

Зная величину i можно легко определить долготу восходящего узла. Из прямоугольного сферического треугольника ADK найдем дугу DK по формуле:

sin (ИDK) =

Если величину этой дуги вычесть из долготы точки A₁, то это и будет долгота восходящего узла:

W = l_A – (ИDK)

Как видно из определения элементов i, W нам потребовались координаты только двух точек A₁ и С₁. Для контроля расчетов можно повторить вычисления по такой же схеме для точек B₁и C₁, A₁ и С₁. Результаты должны совпадать. При неизбежных небольших разбросах три полученные результата усредняют (лучше обработать на основе способа наименьших квадратов).

Чтобы определить время прохождения АМС через перигелий T₀ , находим первоначально эксцентрическую аномалию E₁:

и далее время движения от перигелия:

Вычтя найденное время от момента наблюдений в точке А₁,

определяем начальную эпоху Т₀:

Т₀ = Т₁ - t₁

где T₁ - момент наблюдения АМС в точке A₁.

Если отмечать моменты прохождения АМС через точки В, С, то для контроля определения начальной эпохи можно провести аналогичные вычисления:

Т₀ = Т₂ - t₂

T₀ = T₃ - t₃

T₂ и T₃- моменты нахождения АМС в точках В, С.

Результаты должны совпадать. При небольшом разбросе результатов для уточнения начальной эпохи их можно усреднить, взяв среднее арифметическое или обработав на основании способа наименьших квадратов.

Не трудно видеть, что по своим возможностям предлагаемая "Карта движения планет" значительно выходит за рамки школьного курса астрономии. Тем не менее, её использование оказывается очень удобным при изучении целого ряда вопросов в рамках не только кружков, факультативных курсов, спецкурсов, спецсеминаров, но и при работе по обязательной программе. В этом случае "Карта Движений планет" будет выступать в роли вспомогательного наглядного пособия.

Так, мы считаем, что "Карту движений планет" целесообразно использовать (если для этого найдутся возможности) для иллюстрации следующих вопросов темы "Введение": "Зависимость вида неба от времени года", "Видимое движение Солнца среди звезд", "Видимые движения планет относительно звезд".

Карта не просто дополняет другие наглядные пособия (например, диафильмы "Звездное небо" и "Видимые движения небесных светил"), но, что является очень важным, позволяет ставить и решать практические задачи на примерах действительно происходящих движений изучаемых светил.

Для таких демонстраций Карту необходимо наклеить на лист толстого картона или фанеры и аккуратно обрезать по окружности. В центре карты, там где расположено Солнце, сверлится небольшое отверстие, в котором закрепляется небольшая металлическая втулка. Карта прибивается к стене так, чтобы она могла легко вращаться вокруг своей оси. Аналогичным образом монтируется и дополнительный лист.

При объяснении вопроса о зависимости вида звездного неба от времени года учитель отмечает соответствующей фишкой положение Земли на какую-то дату и поясняет, что на ночном полуночном небе будут видны те созвездия, направление на которых противоположно направлению на Солнце. Так, например, чтобы определить примерный вид полуночного звездного неба 1 января, находим на орбите Земли (см. приложение - "Карту движений планет") дату 1 января. Фишкой отмечаем это положение Земли на её орбите. Проводим мысленную прямую через центр Солнца и через центр фишки, отмечающей положение Земли. Находим точки пересечения этой прямой с эклиптикой. Они лежат в созвездиях Скорпиона и Близнецов. Тогда можно понять, что для земного наблюдателя 1 января Солнце видно на фоне созвездия Скорпиона, а на южной части неба вблизи полуночи мы сможем увидеть созвездия Ориона, Тельца, Б. Пса и т.д.

Если провести аналогичные определения на какую-то другую дату (например, 10, 20, 30 января), то ученик легко увидит, что вид звездного неба и видимое положение Солнца среди звезд изменяются, и поймет, что оба эти явления есть следствие действительного движения Земли вокруг Солнца по своей орбите.

При объяснении вопроса о видимых движениях планет с использованием "Карты движений планет" целесообразно, прежде всего, показать учащимся, что угловые удаления внутренних планет от Солнца не могут превышать некоторой определенной для данной планеты величины. Для этого отмечаем на карте соответствующей фишкой произвольное положение Земли. Считая для простоты рассуждений Землю в дальнейшем неподвижной, показываем учащимся, что при любом возможном положении внутренней планеты на своей орбите её угловое удаление от Солнца не может быть больше чем 28њ для Меркурия и 47њ для Венеры. Очень важно подчеркнуть, что такие рассуждения позволяют предсказать условия видимости внутренних планет, - они могут наблюдаться только как утренние или вечерние светила и никогда не могут находиться в точке небосвода, противоположной Солнцу.

После таких объяснений полезно сделать несколько упражнений на определение условий видимости внутренних планет.

Например, определим условия видимости Венеры 10 сентября 1973 года. Для этого находим на орбите Земли (см. приложение - "Карту движений планет") ту точку, в которой находится Земля 10 сентября. По известной гелиоцентрической долготе, которая взята из таблицы N14 приложения к диссертации, определяем действительное положение этой планеты на её орбите (см. п.2 стр.162). Гелиоцентрическая долгота Венеры - 40⁰,1. Соответствующими фишками отмечаем положение Земли и Венеры на орбитах. Тогда для ученика становится понятным, что для земного наблюдателя Венера "видна" почти в направлении Солнца и примерно на 3⁰ выше его, если учесть значение гелиоцентрической широты планеты.

Очень полезно проследить видимое перемещение какой-либо из внутренних планет в течение длительного промежутка времени (несколько месяцев текущего года). Методика проведения таких построений была описана выше (см. п. 5"а"). Если построить целую серию последовательных видимых положений планеты с интервалом, предположим, 5 суток, то ученик сможет нарисовать траекторию видимого перемещения планеты на фоне звезд на любой заданный промежуток времени. Сознания того факта, что он предначертал путь планете, с которого она не сможет сойти, имеет для него громадное мировоззренческое значение.

Совершенно аналогичные рассуждения и иллюстрации можно провести и при изучении видимых перемещений и условий видимости внешних планет. В этом случае часто придется пользоваться вторым вспомогательным листом "Карты движений планет".

Как мы уже указывали ранее, очень полезным оказывается использование "Карты движений планет" при изучении многих вопросов, связанных с движениями искусственных тел солнечной системы. Если при работе по обязательным школьным программам недостаток времени не позволяет полностью использовать возможности данного пособия, а заставляет рассматривать его как вспомогательное, то при изучении целого ряда тем на занятиях астрономических кружков, спецкурсов, спецсеминаров или факультативных практикумов "Карта движений планет" может оказаться решающим, а зачастую и единственным пособием такого рода.

В случае углубленного изучения материала (например, в рамках факультативного курса "Основы космонавтики") целесообразно использовать метод группового или индивидуального решения задач с помощью карты. Для более бережного обращения с пособием все построения необходимо производить не на карте, а на листе кальки, положенной поверх карты.

¹ А.Д.Марленский, Е.И. Ковязин. Карта движений планет. М., "Наука", 1971 г.
²Михайлов А.А. Звездный атлас. Четыре карты звездного неба до 40 градусов южного склонения. Изд-во АН СССР, 1958 г.

<< Предыдущая

Содержание

Следующая >>