 |
Астронет: Е.И. Ковязин Место, содержание и методика преподавания вопросов движения небесных светил в курсе астрономии средней школы http://www.astronet.ru/db/msg/1173487/chapter3.html |
| << Предыдущая |
§ 3. Предлагаемая программа.
Таким образом, перед нами встает очередная проблема - каким образом исправить те недостатки, которые выявились в ходе анализа и педагогического эксперимента по действующей сейчас школьной программе по астрономии.
Что касается последнего вывода из анализа программы, мы уже рекомендовали проведение вступительной беседы по простейшим картинам мироздания перед началом изучения курса астрономии в 10-м классе.
Первые три отмеченные нами слабые стороны действующей программы можно исправить, во-первых, изменением объема материала вводных вопросов курса астрономии и, во-вторых, (и это главное) - изменением последовательности изложения материала в них.
Ниже нами предлагается проект программы вводных вопросов курса астрономии в средней школе:
- Звездное небо.
- Различия звезд по блеску и цвету.
- Суточные движения светил на различных широтах.
- Восход, кульминация и заход светил.
- Горизонтальные координаты.
- Экваториальные координаты.
- Созвездия.
- Звездные карты, изображения звезд на них.
- Зависимость вида неба от времени года.
- Видимое движение Солнца среди звезд.
- Видимое движение Луны среди звезд.
- Видимые движения планет среди звезд.
- Основные единицы измерения времени.
Для того, чтобы можно было более определенно говорить о преимуществах предлагаемой программы темы "Введение", проведем опять-таки матричное исследование её, аналогичное тому, которое мы проводили над действующей сейчас программой. Прежде всего необходимо отметить, что по объему материала предлагаемая нами программа отличается от действующей ныне введением только одного вопроса - "Горизонтальные координаты". Кроме того, вместо вопроса "Зависимость вида неба от положения наблюдателя на Земле" предлагается поставить вопрос "Суточные движения светил на различных широтах" как более глубокий и более целесообразный.
Итак, наша матрица будет содержать 13 строк и 13 столбцов. Покажем на примерах рассмотрения всех позиций порядок заполнения клеток матрицы:
- "Звездное небо" - исходная позиция
- "Различия звезд по блеску и цвету" - для объяснения материала этой позиции необходимо опираться на материал только 1-ой ("Звездное небо") позиции.
- "Суточные движения светил на различных широтах" - для объяснения материала этой позиции необходимо привлечь сведения только 1-ой ("Звездное небо") позиции
- "Восход, кульминация и заход светил" - для объяснения материала этой позиции необходимо привлекать материал 1-ой и 3-ей позиции.
- "Горизонтальные координаты" - для объяснения этого материала мы должны использовать понятия и материал 1-ой, 3-ей и 4-ой позиций.
- "Экваториальные координаты" - 1-ая, 2-ая, 4-ая позиции.
- "Созвездия" - 1-ая, 2-ая и 6-ая позиции.
- "Звездные карты, изображения звезд на них" - 1-ая, 2-ая, 7-ая и 6-ая.
- "Зависимость вида неба от времени года" - 1-ая,3-ая, 7-ая, 4-ая, 2-ая и 6-ая позиции.
- "Видимое движение Солнца среди звезд" - 1-ая,3-ая, 4-ая, 7-ая, 2-ая и 6-ая позиции.
- "Видимое движение Луны среди звезд" - 1-ая, 2-ая, 3-ья, 4-ая, 6-ая, 7-ая, 9-ая и 10-ая позиции.
- "Видимые движения планет среди звезд" - позиции 1,2,3,4,6,7,9 и10.
- "Основные единицы измерения времени" - позиции 1,2,3,4,6,7,9 и 10.
 |
|
матрица 2 |
Таким образом, мы снова получим матрицу, определенные клетки которой заштрихованы. Исходя из анализа данной матрицы, определим "ПОСЛЕДОВАТЕЛЬНОСТЬ" и "НЕРАЗРЫВНОСТЬ" предлагаемого нами варианта программы этой части курса.
1. Поскольку в нижней половине матрицы
отсутствуют штрихованные клетки, то m = 0, n = 0.
Тогда, согласно соотношению 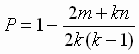 ,
P = 1;
,
P = 1;
"Последовательность" построения
предлагаемого нами варианта учебной
программы равняется единице.
2. Нетрудно подсчитать, что число клеток p,
характеризующих "Неразрывность"
построения предлагаемой программы
равняется р=6. Тогда согласно соотношению 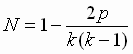 ,
N » 0.9
,
N » 0.9
"НЕРАЗРЫВНОСТЬ" построения предлагаемого нами варианта учебной программы равняется примерно 0,9.
Таким образом, основные характеристики предлагаемой нами программы вводных разделов астрономии превосходят аналогичные характеристики действующей сейчас школьной программы по астрономии (1,0 и 0,9 против 0,7 и 0,8). Безусловно, можно говорить о том, что подобная картина анализа и следующие из нее исправления не являются абсолютно правильными и полными. Поясним это на примере.
Если поменять местами 5-ую и 6-ую позиции, то вновь полученный порядок расположения материала может сказаться либо более, либо менее удобным в работе для отдельного педагога, чем предлагаемый нами вариант. Тем не менее, на наших соотношениях (если бы мы их рассчитали для вновь полученной матрицы) это никак не отразится. Возможно, кто-либо из учителей или методистов заинтересуется этим, хотя и сугубо частным, но достаточно интересным вопросом, и сможет аналитически подтвердить такие подсознательные, интуитивные предпочтения.
Очевидно, этот вопрос является частным случаем очень интересной и мало исследованной проблемы психологической организаций учебного материала. Некоторые общепедагогические разработки в этом плане уже имеются [83], но частные методики, насколько нам известно, подобными вопросами занимаются очень мало. Мы также оставляем эту проблему в стороне, тем более что её решение не входит в задачу настоящего исследования.
Более того, очевидно, требования психологической организации учебного материала могут оказаться столь сильными, что иногда смогут оттеснять на второй план требования логически стройного расположения материала. Это становится возможным, конечно, только в рамках определенных нестрогостей и условностей.
Например, если в нашем случае 7-ую позицию переставить на третье место, то многие учителя астрономии согласятся с тем, что вновь полученный порядок расположения учебного материала в условиях средней школы окажется более приемлемым. Но при этом придется первоначально дать определения понятия созвездия как участка на поверхности небесной сферы, не уточняя того факта, что строгие его границы определяются сеткой экваториальных координат. Именно такой вариант программы был использован нами в опытном двухгодичном обучении. Ниже он приводится:
"Звездное небо. Различия звезд по блеску и цвету. Созвездия. Суточные движения светил на различных широтах. Восход, кульминация и заход светил. Горизонтальные координаты. Экваториальные координаты. Звездные карты и изображения звезд на них. Зависимость вида звездного неба от времени года. Видимое движение Солнца среди звезд. Видимое движение Луны среди звезд. Видимые движения планет относительно звезд. Основные единицы измерения времени".
Легко понять, что выбор такого варианта учебной программы не был достаточно аргументирован только в одном плене - был оставлен в стороне вопрос о соотношениях между требованиями логичности и неразрывности программы курса с требованиями психологической организации учебного материала.
Нам представляется оправданной следующая взаимосвязь между этими критериями. В подавляющем большинстве случаев на первое место необходимо ставить требование создания логически стройного курса с возможно меньшим числом временных разрывов.
Требования психологической организации могут выступать на первый план только тогда, когда возможно такое неполное (или не совсем строгое) объяснение изучаемого вопроса, которое в дальнейшем будет только уточняться, но не отрицаться. Имея это в виду, Л.И. Резников писал: "Процесс формирования научного понятия многогранен. Не всегда имеются педагогические возможности дать определение понятая с такой полнотой, чтобы в дальнейшем не приходилось в корне его изменять".1
Необходимость такого шага в каждом конкретном случае будет определяться методикой изложения данного вопроса и привычными методическими приемами педагога. Можно указать еще на некоторые возможности применения результатов матричного анализа в работе учителей и методистов.
1. Распределение штрихованных клеток по строкам матрицы говорит о частоте использования материала той или иной позиции, а значит и о важности его в общем курсе. Поэтому такие позиции в первую очередь нуждаются в оснащении их необходимыми наглядными пособиями. Так, например, в матрице 2 можно рекомендовать изготовление наглядных пособий по материалам позиций 1, 2, 3, 4, 6, и т.д.. Необходимо отметить, что подобные выводы можно делать только (и то очень осторожно) из анализа матриц с достаточно большим количеством позиций и только в отношении небольшого числа первых позиций. В противном случае могут быть получены не совсем правильные выводы, ибо само местоположение последних позиций исключает большое число ссылок на них, а значит и рекомендаций на изготовление наглядных пособий по материалам этих позиций. По-видимому, встречающееся в методической литературе утверждение о том, что по числу заполненных клеток в строке можно говорить о мобильности необходимого наглядного пособия [26], иллюстрирующего эту позицию, по приведенным выше соображениям является не совсем четким и правильным. Очевидно, более точным будет требование создания для иллюстрации вопросов, на которые в дальнейшем мы ссылаемся очень часто, таких пособий, которые были бы не столько максимально мобильными, сколько максимально действенными.
2. Если в распоряжении педагога имеется заполненная по данной теме курса матрица, то он всегда сможет быстро сориентироваться в том, какой материал необходимо повторить учащимся, чтобы успешно усвоить материал нового урока. Например, при изучении на будущем уроке позиции 13 ("Основные единицы измерения времени") учителю целесообразно задать на дом повторять материал 3-ей ("Суточные движения светил на различных широтах"), 4-ой ("Восход, кульминация и заход светил"), 6-ой ("Экваториальные координаты"), 8-ой ("Зависимость вида звездного неба от времени года") и 10-ой ("Видимое движение Солнца среди звезд") позиций, или хотя бы наиболее важных из них.
Таким образом, использование матричного
метода при анализе программ курсов
позволяет не только получить
количественные оценки качеств построения
программ, но и оказывается удобным на
главных этапах подготовки к процессу
обучения:
а) при составлении учебных программ и
оценке их;
б) при разработке необходимых наглядных
пособий;
в) при подготовке к уроку.
Необходимо отметить также, что, очевидно, существуют определенные взаимоотношения между предлагаемым применением матричного метода и различными не только методическими школами, но и даже приемами, которыми пользуются при объяснении того или иного вопроса. В зависимости от того, какими методическими приемами пользуется методист, применяющий матричный метод к анализу качества программ - конечный результат может отличаться от полученного нами. Однако, такие соображения не могут привести к отрицанию подобной методики вообще.
Таким образом, в первой главе диссертации решены следующие задачи:
1. Показано, что в сложившихся условиях вопросы сферической и практической астрономии должны быть сведены к изучению общих закономерностей видимых движений небесных светил. Такой подход является наиболее целесообразным первым шагом в изучении закономерностей движений небесных светил, овладение которыми - очень важный этап в раскрытии философского содержания термина "движение", а, значит, в формировании материалистического мировоззрения школьника.
2. Разработан математический метод, позволяющий получить количественные критерии для оценок и составления учебных программ.
3. В результате применения этого метода к анализу действующей школьной программы по астрономии выявлены некоторые недостатки программы и предложены пути их исправления. Предлагается вариант программы вводных вопросов школьного курса астрономии.
4. Показана необходимость проведения вступительной беседы по основам астрономии перед началом изучения этого курса. Определено содержание беседы.
1 Л.И.Резников. Выступление на совещании по обсуждению новых школьных программ. "Физика в школе", №5, 1969 г.
| << Предыдущая |