 |
Астронет: Е.И. Ковязин Место, содержание и методика преподавания вопросов движения небесных светил в курсе астрономии средней школы http://www.astronet.ru/db/msg/1173487/chapter2.html |
| << Предыдущая |
§2. Анализ организации материала вводных вопросов в новой школьной программе.
После того, как мы определили объем и глубину изложения вводных вопросов темы "Введение" (т.е. после решения проблемы отбора учебного материала), попытаемся проанализировать организацию материала в программу этой части курса астрономии средней школы.
Под проблемой организации учебного материала мы понимаем выбор такой последовательности расположения его вопросов, которая бы обеспечила бы оптимальный вариант учебной программы.
Знакомство с педагогической и частнометодической литературой показало, что подавляющее большинство требований к организации учебного материала вводится к соблюдению логики учебного материала и логики процесса познания. Между тем организация учебного материала - одна из основных задач не только частнометодических, но и педагогических исследований, должна пониматься более глубоко и в то же время более конкретно.
Для оценки качества организации материала в учебных программах нами предлагается использовать три критерия: психологическую организацию, последовательность и неразрывность.
Вопросы психологической организации учебного материала были проанализированы В.В. Репкиным [83].
Остановимся подробнее на критериях "последовательность" и "неразрывность".
Изучение педагогической литературы [22, 26, 76, 91] подсказало нам наглядный и удобный, на наш взгляд, метод анализа качества построения программ курса или отдельных тем его. Речь идет о так называемом матричном методе. Первоначально он был введен и успешно апробирован для разработки и выделения отдельных вопросов-позиций при программированном обучении. [91]
Мы попытаемся применить его к анализу построения курса вообще и вводных вопросов астрономии в частности . Насколько нам известно, раньше подобных попыток не предпринималось .
Выделим те вопросы-позиции, которые относятся непосредственно к вводным вопросам астрономии, и расположим их в том порядке, как это делает новая программа:
1. Звездное небо
2. Вращение звездного неба.
3. Изображение звездного неба на звездных
картах.
4. Созвездия.
5. Различие звезд по блеску и цвету.
6. Кульминация, восход и заход светил на небе.
7. Видимое движение Солнца среди звезд.
8. Видимое движение Луны относительно звезд.
9. Видимое движение планет относительно
звезд.
10. Экваториальные координаты.
11. Зависимость вида неба от времени года.
12. Зависимость вида неба от положения
наблюдателя на Земле.
13. Основные единицы измерения времени.
Составим квадратную таблицу – матрицу, - состоящую из 13 строк и 13 столбцов. При заполнении клеток матрицы будем руководствоваться следующим соображением: если для того, чтобы объяснить ученику, предположим, 13-ую позицию ("Основные единицы измерения времени") учитель должен в той или иной мере обратиться к понятиям и материалу 1-ой ("Звездное небо"), 2-ой ("Вращение звездного неба"), 7-ой ("Кульминация, восход и заход светил"), 8-ой ("Видимое движение Солнца среди звезд") и 12-ой ("Зависимость вида неба от времени года") позиций, то в 13-ом столбце мы заштриховываем клетки строк 1, 2, 7, 8, 12.
Мы будем в дальнейшем исходить из того, что полное (в рамках требований какой-то программы) объяснение вопроса в педагогической и дидактической точек зрения целесообразнее осуществлять по возможности сразу, не оставляя непонятных оговорок и моментов на последующие уроки. При объяснении любого вопроса необходимо по возможности реже прибегать к таким ситуациям, когда учитель вынужден говорить учащимся, чтобы они пока просто запомнили излагаемые им сведения, а понять их полностью они смогут позднее, после изучения еще какого-то материала. В методической литературе неоднократно отмечалась вредность подобных ситуаций. В частности, С.Л. Рубинштейн писал: "Усвоение знаний, за которым не стоит аналитико-синтетическая работа мысли, - то и есть знание минус мышление, или, поскольку никакое усвоение знаний невозможно без мышления, знания плюс неадекватный им минимум мышления".1
 |
|
матрица 1 |
Покажем на примерах всех позиций порядок заполнения клеток матрицы по столбцам:
1. "Звездное небо - исходная позиция.
2. "Вращение звездного неба" - для объяснения материала этой позиции мы должны привлечь сведения только 1-ой позиции. Поэтому во втором столбце матрицы заштриховывается только первая клетка.
3. "Изображение звездного неба на звездных картах" - для полного объяснения (в рамках требований новой программы) этого материала мы должны использовать понятия и сведения 1-ой ("Звездное небо"), 4-ой ("созвездия"), 5-ой ("Различия звезд по блеску и цвету) , 10-ой (Экваториальные координаты) позиций и 2-ой.
4. "Созвездия" - для объяснения материала этой позиции необходимо оперировать материалом 1-ой ("Звездное небо"), 5-ой ("различие звезд по блеску и цвету") и 10-ой ("Экваториальные координаты") позиций и 2-ой.
5. "Различия звезд по блеску и цвету" - при изложении материала этой позиции учителю придется опираться на материал только 1-ой ("Звездное небо позиции").
6. "Кульминация, восход и заход светил" - при объяснении этого материала учитель будет вынужден обращаться к материалу и понятиям 1-ой ("Звездное небо") и 2-ой ("Вращение звездного неба позиций").
7. "Видимое движение Солнца среди звезд" - для понимания этого вопроса школьник должен знать материал 1-ой ("Звездное небо"), 2-ой ("Вращение звездного неба"), 4-ой ("Созвездия"), 6-ой ("Кульминация, восход и заход светил"), 11-ой ("Зависимости вида звездного неба от времени года") позиций. Кроме того, поскольку знание 4-ой ("Созвездия") позиции невозможно (см. п. 4) без знания 5-ой ("Различия звезд по блеску и цвету") и 10-ой ("Экваториальные координаты") позиций, то в этом столбце мы должны, кроме перечисленных выше, заштриховать еще 5-ую и 10-ую клетки.
8."Видимое движение Луны относительно звезд". Изложение данного вопроса в новом школьном учебнике производится на основании сравнения видимого движений Луны с видимым движением Солнца. Поэтому в этом столбце мы штрихуем все клетки, что и в предыдущем ("Видимое движение Солнца среди звезд") и, кроме того, клетку 7-ой строки.
9."Видимое движением планет относительно звезд" - при объяснении материала этой позиции учитель в качестве опорного будет использовать материал тех же позиций, что и при изучении вопросов-позиций "Видимое движением Солнца среди звезд" и "Видимое движение Луны среди звезд". Поэтому в этом столбце мы должны заштриховать клетки строк 1, 2, 4, 5, 6, 7, 8,9,10 11.
10. "Экваториальные координаты" - для полного знакомства школьника с этим вопросом в объеме требований новой программы по астрономии, как показали наши исследования, вполне достаточно опираться на материал 1-ой ("Звездное небо") и 2-ой ("Вращение звездного неба") позиций.
11. "Зависимость вида звездного неба от времени года" - для ознакомления школьника с этим материалом учитель будет опираться на материал 1-ой ("звездное небо"), 2-ой ("вращение звездного неба"), 4-ой ("Созвездия") и 6-ой ("Кульминация, восход и заход светил") позиций. Кроме того. так как изложение 4-ой ("Созвездия") позиции опирается на материал 5-ой ("Различие звезд по блеску и цвету и 10-ой ("Экваториальные координаты") позиций, то мы должны также заштриховать клетки 5-ой и 10-ой строк этого столбца.
12. "Зависимость вида звездного неба от местоположения наблюдателя на Земле" - при изложении материала этой позиций учитель будет опираться на сведения 1-ой ("Звездное небо"), 2-ой ("Вращение звездного неба"), 4-ой ("Созвездия") и 6-ой ("Восход, кульминация и заход светил") позиций. Кроме того, по причинам, упоминаемым в предыдущем пункте, мы должны включить в этот список 5-ую и 10-ую позиции.
13. "Основные единицы измерения времени" - при объяснении этого вопроса в объеме требований новой программы учитель будет опираться на понятия и материал 1-ой ("Звездное небо"), 2-ой ("Вращение звездного неба"), 6-ой ("Восход, кульминация и заход светил на небе") и 7-ой ("Видимое движение Солнца среди звезд") позиций. Кроме того, так как для объяснения материала 7-ой позиции мы используем сведений 10-ой ("Экваториальные координаты") и 4-ой ("Созвездия"), 5-ой ("Различия звезд по блеску и цвету") и 2-ой ("Зависимость вида звездного неба от времени года") позиции, то в этом столбце мы должны, кроме перечисленных выше, заштриховать клетки 4-ой. 5-ой. 10-ой и 11-ой строк.
Таким образом, была получена матрица, определенные клетки которой заштрихованы.
Не трудно видеть, что в случае последовательно построенного курса в матрице будут штриховаться только те клетки, которые лежат над диагональю матрицы. Если заштрихованная клетка лежит под диагональю матрицы, то это значит, что для объяснения какого-то вопроса необходимо использовать материал позиций, которые будут изучаться позднее.
Можно видеть, что в нашем случае наблюдается некоторая непоследовательность построения курса. Действительно, например, объяснение 3-ьей позиции ("Изображение звездного неба на звездных картах") невозможно без знания материала позиций 4-ой ("Созвездия"), 5-ой ("Различия звезд по блеску и цвету") и 10-ой ("Экваториальные координаты").
В принципе подобный метод исследований построений курса достаточно понятен и не является чем-то особенным. Подобные выводы можно получить и при простом вдумчивом анализе построения курса. Но нельзя не считать его наглядным, убедительными и позволяющим охватить всю картину анализа в целом.
Кроме того, такое картинное представление результатов анализа имеет ещё одну положительную сторону. Оно может показать некоторые недостатки построения курса даже в том случае, если он безупречен с точки зрения последовательности построения его.
Действительно, в идеальном случае мы должны иметь матрицу с полностью заштрихованными клетками верхней её половины. Отсутствие заштрихованных клеток в нижней половине матрицы говорит о логичности построения курса, а полное заполнение - о таком построении его, когда для объяснений каждой последующей позиции необходимо обязательно привлекать материал предыдущей позиции, а значит и всех предыдущих.
В реальных курсах такой случай, конечно, не реализуется, но, тем не менее, подобные соображения позволяют нам сделать некоторые выводы не только о логичности построения курса, но и о его разрывности.
Действительно, если для объяснения, например, 6-ой позиции ("Кульминация, восход и заход светил") необходимо привлечь материал только 1-ой ("Звездное небо") и 2-ой ("Вращение звездного неба") позиций и совершенно не используется материал 3-ей ("Изображение звездного неба на звёздных картах"), 4-ой ("Созвездия") и 5-ой ("Различия звезд по блеску и цвету") позиций, то 6-ую позицию целесообразно перенести на 3-е место. Подобный разрыв двух непосредственно связанных между собой вопросов - "Вращение звездного неба" и "Восход, заход и кульминация светил", - материалами нескольких уроков, явно говорит о некоторой прерывности курса.
С нашей точки зрения представляется очень интересным и важным введение некоторых количественных величин, характеризующих качество построения курса. Назовем эти величины "ПОСЛЕДОВАТЕЛЬНОСТЬ" и "НЕРАЗРЫВНОСТЬ".
"Последовательность" в простейшем
случае мы смогли бы количественно
охарактеризовать дробью, в числителе
которой проставлено число штрихованных
клеток в нижней половине матрицы, а в
знаменателе - полное число клеток в
половине матрицы. Тогда, если:
m - число заштрихованных клеток в нижней
половине матрицы,
k - число позиции в матрице,
то "Последовательность" можно
охарактеризовать дробью: 
Покажем, что такая характеристика будет не совсем полной и точной. Из анализа матрицы 1 видно, что мы ссылаемся раньше времени на 4-ую позицию (см. 4-ую строку нижней половины матрицы) только один раз - при объяснении материала третьей позиции. На 10-ую позицию преждевременно мы ссылаемся пять раз - при изучении 3-ей, 4-ой, 7-ой, 8-ой и 9-ой позиций. Т. е. одна не на месте стоящая позиция вызывает необходимость штриховать различное количество клеток в нижней половине матрицы.
Поэтому более полно "Последовательность"
нужно характеризовать суммой двух дробей.
Одна из них приведена выше, а другая будет
иметь вид ![]() ,
,
где: n - число позиций, клетки которых
штрихованы в нижней половине матрицы.
Сумма их:  .
.
Не трудно видеть, что последняя дробь
будет изменяться от 0 до 2. В идеально
хорошем случае (по нашим представлениям -
это такой вариант программы какого-то курса,
когда каждый последующий вопрос вытекает
только из каждого предыдущего, а значит и из
всех предыдущих) в матрице будет
заштрихована только ее верхняя половина и m
= n = 0. Тогда дробь будет также равна нулю. В
идеально плохом случае (когда будут
заштрихованы все клетки только нижней
половины матрицы) -  ;
;
![]() , - дробь
будет равняться двум.
, - дробь
будет равняться двум.
Более привычной ситуацией для нас будет такая, когда "ПОСЛЕДОВАТЕЛЬНОСТЬ" более удачно составленной программы будет выражаться не меньшим, как в нашем случае, а большим положительным числом.
Поэтому в окончательном виде "
ПОСЛЕДОВАТЕЛЬНОСТЬ " - в дальнейшем - P -
условимся характеризовать соотношением:
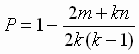 (1)
(1)
Не трудно видеть, что "ПОСЛЕДОВАТЕЛЬНОСТЬ" принимает значение P=1 в том случае, если m=0 и n= 0. Это соответствует случаю логически безупречного построения курса.
В другом крайнем случае (если представить
себе такую невозможную картину), когда
заштрихованы все клетки только нижней
половины матрицы, т. е.  ;
;
![]() ,
,
то в этом случае: P=0.
Фактически это случай изложения логически стройного и идеально неразрывного (понимание нами термина "неразрывность" раскрывается подробно ниже) курса с конца.
Таким образом, величина P - "ПОСЛЕДОВАТЕЛЬНОСТЬ" построения программы курса может изменяться в пределах от 0 до 1. Очевидно, в действительности будут реализоваться такие ситуации, когда 0 < Р Ј 1
Введенная нами выше величина Р - "ПОСЛЕДОВАТЕЛЬНОСТЬ не может дать нам полного представления о качестве построения программы.
Действительно, программа может быть построена логически безупречно (т. е. Р=1), но при этом могут наблюдаться такие случаи, как, например, случай с позициями 6 и 10 в матрице 1. При объяснении материала этих позиций учитель будет опираться только на материал 1-ой и 2-ой позиций. Поэтому нет никакой не только необходимости, но и целесообразности помещать эти позиции на 6-ое и 10-ое места. Их можно поставить на 3-е и 4-ое места. Это, во-первых, позволит уменьшить временно разрыв в изучении двух связанных между собой позиций и, во-вторых, (это можно легко показать) приведет к увеличению величины P.
Другую количественную характеристику качества построения программ курсов мы называем "НЕРАЗРЫВНОСТЬ". Её введение диктуется необходимостью более полной количественной характеристики программы курса.
Нетрудно понять, что величину N - "НЕРАЗРЫВНОСТЬ
можно достаточно полно и однозначно
характеризовать числом свободных клеток
между самой нижней штрихованной клеткой
данного столбца и диагональю матрицы.
Обозначим это число - р. Тогда величину N
можно определить из соотношения:
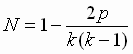 (2)2
(2)2
Если каждый вопрос курса сугубо
самостоятелен и не связан ни о одной из
ранее излагаемых позиций (этот фиктивный
случай представляет чисто теоретический
интерес и в реальных курсах, конечно, нt
реализуется), то не трудно видеть, что в этом
случае величина N = 0, т. к.  матрица будет совсем незаполненной, чистой.
матрица будет совсем незаполненной, чистой.
Если каждый последующий вопрос вытекает только из предыдущего (а значат и из всех предыдущих), то в этом случае будет штриховаться вся верхняя половина матрицы и p = 0. Тогда: N = 1
Такой случай также практически вряд ли возможен.
Очевидно, в действительности будут реализоваться такие ситуации, когда 0<N<1.
Определим величины P и N для действующей
сейчас новой школьной программы по
астрономии. Из анализа матрицы находим:
k=13; m=11; n=4; p=17.
Тогда: P»0,7; N»0,8.
Мы выбрали пределы изменения основных
характеристик качества построения
программ от 0 до 1 произвольно. При желании
можно перейти к любой другой шкале оценок.
Для этого в соотношения 1 и 2 необходимо
ввести множитель – постоянное число,
максимально возможное в выбранной шкале
оценок. Так, если эти соотношения записать:
 ,
,
то величины P и N будут изменяться в
пределах от 0 до 5.
Не трудно показать, что обе введенные нами величины P и N являются тесно связанными между собой. Не являясь единственно возможными характеристиками, они все же достаточно полно характеризуют качество построения программ. Но тот факт, что программа будет характеризоваться двумя величинами, может быть чреват некоторыми нежелательными последствиями. В самом деле (если отвлечься от других методов анализа и от других оценок программ), какой из двух предложенных программ курса отдать предпочтение, если, например, для первого варианта программы P1=1.0; N1=0.5, а для второго P2=0.8; N2=0.7.
Следует оговорить также, что мы довольно аксиоматично приняли соображение о том, что эти величины обладают одинаково важной характеризующей способностью. Достоверность подобного соображения можно считать проблематичной и спорной, но, во всяком случае, все доводы, как "за", так и " против", в большой степени неопределенны и субъективны.
Кроме того, следует помнить, что величины P и N, хоть и не в значительной степени, зависят от разбивки темы на позиции, от масштабности каждой позиции, а значит и от числа позиций по данной теме.
Но существуют некоторые закономерности в применении предлагаемого метода анализа качества построения программ, которые в значительной степени сводят к минимуму как субъективные ошибки, возникающие при выделении отдельных позиций, так и слабые стороны, присущие предлагаемым соотношениям вообще.
Дело в том, что данный метод целесообразно применять всегда для сравнивания каких-то программ, составленных из одинаковых позиций. Поэтому субъективные аспекты и некоторые "нестрогости" метода будут примерно в одинаковой количественной степени сказываться на результатах исследования как опытного, так и контрольного курсов.
Таким образом, в результате проведенного исследования новой школьной программы по астрономии мы убедились, что ей присущи некоторые недостатки, снижающие педагогическую действенность ее. Речь идет о следующих моментах:
1. Довольно существенным недостатком принятой программы является некоторая непоследовательность ее. Действительно, из анализа матрицы 1 видно, что часть штрихованных клеток находится ниже диагонали матрицы. Это (как мы показали ниже) говорит о непоследовательности построения программы. Отметим такие " непоследовательные" позиции:
"Изображение звезд на звездных картах – (позиция 3) - при изложении материала этой позиции необходимо опираться на материал и понятия 4-ой ("Созвездия"), 5-ой ("Различие звезд по блеску и цвету") и 10-ой ("Экваториальные координаты") позиций, которые будут излагаться на последующих уроках.
"Созвездия" - (позиция 4) - объяснение этого вопроса невозможно без ссылок на материал 5-ой ("Различия звезд по блеску и цвету") и 10-ой ("Экваториальные координаты") позиций, которые излучаются позднее.
"Видимое движение Солнца среди звезд" - ( позиция 7) - полное ( в объеме требований действующей школьной программы) объяснение этого вопроса невозможно без ссылок на материал 10-ой ( "Экваториальные координаты") и 11-ой ( "Зависимость вида звездного неба от времени года") позиций, которые излучаются позднее.
"Видимое движение Луны среди звезд" - ( позиция 8). При изложении этого вопроса необходимо знание материала 10-ой ("Экваториальные координаты") и 11-ой ("Зависимость вида звездного неба от времени года") позиций, излучаемых позднее.
"Видимое движение планет относительно звезд" - (позиция 9) - объяснение материала этой позиции требует оперирования материалом и понятиями позднее изучаемых (не считая изучаемых ранее) 10-ой ("Экваториальные координаты") и 11-ой ("Зависимость вида звездного неба от времени года") позиций.
2. Другим недостатком данной программы являются элементы разрывности. ("Кульминация, восход и заход светил") требуется оперирование материалом только 1-ой ("Звездное небо") и 2-ой ("Вращение звездного неба") позиций. Нет никакой необходимости помешать эту позицию на 6-е место, тем более, что она следует прямо из 2-ой ("Вращение звездного неба") позиции.
Еще более нагляден пример с 10-ой позицией ("Экваториальные координаты"). Для её объяснения необходимо оперировать понятиями и материалом только 1-ой ("Звездное небо") и 2-ой ("Вращение звездного неба") позиций. Почему же вопрос об экваториальных координатах отодвинут на 10-е место, а не находится ни третьем ни на четвертом месте? Тем более что перемещение его на третье или четвертое место уменьшит число штрихованных в нижней половине матрицы клеток, что приведет к увеличению величины "ПОСЛЕДОВАТЕЛЬНОСТИ" программы (это можно легко показать).
3. Следующим (на наш взгляд) существенным недостатком новой программы является то, что она, как это ни странно, не предполагает знакомства школьника с горизонтальными координатами. Тем более, что это не просто желательно, а совершение необходимо по следующим соображениям:
а) изучение основ сферической астрономии согласно требованиям новой программы должно базироваться на практических наблюдениях школьников. Во время практических наблюдений, желаем мы того или не желаем, положение светил или каких-либо других объектов мы отмечем всегда по отношении к плоскости горизонта, говорим об определенной "высоте" их и положению по отношению к сторонам свети.
б) Школьные кабинеты астрономии вскоре будут оснащаться школьным теодолитом [174, 189], работа с которым требует знания системы горизонтальных координат.
в) Мы не имеем права забывать о большом военно-патриотическом значении этого вопроса. Умение ходить по азимуту, ориентироваться по сторонам света под открытым небом, умение приблизительно определять горизонтальные координаты объектов - эти качества совершенно необходимы будущему воину.
И.Д. Ильевский отмечает: "Если несколько лет назад понятие астрономических координат относилось к суть академическим, то сегодня понятие об этих координатах становится необходимым каждому грамотному человеку, читающему журналы, интересующемуся последними достижениями науки и техники" [162].
Поэтому вопрос о горизонтальных координатах должен быть обязательно включен в новую школьную программу по астрономии.
В связи с этим необходимо отметить печальную судьбу этого вопроса во время перестройки школьной программы по астрономии. Дело в том, что в проект программы, предложенный для обсуждения общественности [168], этот вопрос был включен. Знакомство с отзывами учителей и методистов на проект программы (В.Д. Кулаков. Е.Л. Корякина, Д.А. Мурашов, А.Н. Кремов, М.У. Тульчинский, Г.С. Яхно, Ш.К. Намитоков, Ю.Н. Клевенский, А.А. Серяков, С.А. Попов и др.) показывает, что против включения этого вопроса никто (!) не возражал. Поэтому в приказе министерства просвещения РСФСР за № 3 от 12.03.1964г., посвященному содержанию учебных программ для средней школы, этот вопрос также оставлен.
Тем не менее, в вышедшей буквально вслед за этим приказом школьной программе по астрономии [148] вопрос о горизонтальных координатах отсутствует. Не понятны ни причина, ни пути того, как это было сделано.
Необходимо отметить ещё одно
обстоятельство, имеющее, как показали наши
исследования, важное методическое значение.
Дело в том, что вновь принятая школьная
программа по астрономии предполагает (это
можно легко понять из внимательного
анализа программы) знание школьником
некоторых начальных сведений из области
астрономии, которые были сообщены ему на
уроках природоведения или географии. Это
следующие факты:
а) Земля - шар. Вращается вокруг своей оси со
скоростью 1 об/сутки в направлении с запада
на восток.
б) Земля обращается вокруг Солнца по орбите,
завершая полный оборот за 1 год.
в) Луна - самое близкое к нам небесное, также
шарообразное тело. Она обращается вокруг
Земли по своей орбите, совершая полный
оборот за один месяц.
г) Вокруг Солнца на резвых расстояниях от
него обращаются и другие планеты.
д) Звезды - очень далекие от нас небесные
светила, подобные нашему Солнцу. Они лежат
на различных расстояниях от нас и излучают
различное количество света.
Педэксперимент показывает, что такими простейшими миропредставлениями владеет большая часть учащихся, начинающих учиться в 10-м классе. Тем не менее, нами была проведена специальная проверочная работа, которая позволила выяснить положение дел в этом плане. Материал этой работы служил нам одновременно предэкспериментальным срезом.
Эта проверка происходила следующим образом. В каждом из восьми выпускных классов на первом уроке проводилось сочинение по астрономии. Темы сочинения: "Мои представления о строении мира". Время, отводимое на работу, - 15 мин. Перед началом сочинения учащимся указывалось, в каком плане оно должно быть построено: ученик должен был показать свое положение в пространстве при переходе ко всё более крупным и крупным системам, и сообщить всё, что ему известно о размерах, составе и строении объектов систем.
Ученики также предупреждаются, что работа внепрограммная, не оценивается, совершенно не учитывается при дальнейшей работе с классом, и для большей убедительности работы не подписывались.
В нашем распоряжении оказалось около 250 сочинений учеников 10-х классов. Анализ этих работ в целом подтвердил наши предположения. Значительная часть школьников успешно справилась с предложенной темой и дала удовлетворительнее по качеству ответы, в которых отражены все или почти все выделенные нами факты. Однако разброс по качеству откатов оказался большим, чем мы ожидали. Некоторые сочинения давали вполне современное, грамотное описание строения, размеров и состава не только Землю и Солнечной системы, но даже Галактики и систем галактик. В качестве примера приведем полностью сочинение ученицы 10"б" класса Нины Б.3
Мои представления о строении мира.
"Наша планета входит в состав Солнечной системы. Вместе с ней в эту систему входят Меркурий, Венера, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон. Из-за некоторых странностей в "поведении" Меркурия существует предположение, что между ним и Солнцем существует ещё одна планета. Она ещё не открыта, но название ей дали Вулкан. На Меркурии земная жизнь не возможна, так как очень высокая температура поверхности. На Венере тоже, т.к. атмосфера Венеры состоит из углекислоты, большое давление. На Юпитере, Сатурне, Уране, Нептуне, Плутоне – атмосфера состоит из метана и водорода, поэтому жизнь, такая как на Земле там не возможна, также как из-за очень низкой температуры. Остается один Марс. У Марса есть атмосфера, в которой присутствует кислород, но она очень разрежена. У Марса два больших спутника, вращающихся вокруг планеты по линии экватора. Причем открыты они совсем не давно. Существует два мнения об этих спутниках: они или искусственные, или естественные. Наша солнечная система входит в состав Галактики. Солнце в Галактике – небольшая звезда – "желтый карлик". Самая ближайшая звезда Галактики - a Центавра (4 световых года). Галактики объединяют огромное количество систем, подобных солнечной, поэтому возможно, что в системе какой-нибудь звезды галактики существует жизнь, подобная земной. Галактик во Вселенной множество. Они всегда в движении. Это видно по изменению цвета спектра. Вселенная всегда изменяется. Звезды рождаются и погибают – "взрываются". Звезда могут посылать электромагнитные волны определенной частоты. В последнее время ученых интересуют квазары. Свет от квазаров очень яркий, расположены они далеко. Значит у тел, испускающих такой свет очень большая масса. Существует мнение, что квазары или звезды с огромной массой, или далекий атомный взрыв, свет от которого идет до нас до сего времени".
Не трудно видеть, что основные замечания, которые можно сделать после знакомства с этим сочинением, будут касаться либо стиля изложения, либо незначительных фактических неточностей. Показательным является также тот факт, что учащиеся, давшие положительные ответы на предлагаемые вопросы, предпочитают больше говорить о Галактике, её строении и составе, о кривизне пространства-времени, о конечности и бесконечности вселенной и т.д. и совсем мало о строении, размерах, составе Земли, Луны, планет и даже Солнечной система. Это может говорить только о том, что последние положения являются для них уже достаточно привычными и не настолько интересными, чтобы заставить детское воображение заинтересоваться ими так, как это происходит со сведениями космологического характера.
С другой стороны, необходимо отметить, правда, небольшое количество, неудовлетворительных ответов, количество неудовлетворительных отметок колебалось в пределах 5%. Эту цифру необходимо считать несколько заниженной по следующим соображениям. Несмотря на то, что примерный план, структура и форма сочинения доводилась до каждого ученика (конечно, без упоминания и уточнения фактического материала), тем не менее, можно было встретиться с достаточно большим количеством таких ответов, которые были безошибочными, но далеко не полными. Это вполне понятно. Учащийся пытается умолчать про те факты, в достоверности которых он не уверен. Этот психологический аспект достаточно силен и никакими вступительными беседами свести на нет его невозможно. И все же в таких случаях нельзя быть уверенным, что мы имеем дело с незнанием материала. Поэтому такие ответы хотя и считались нами неполными, но в число отрицательных не вносились.
В качестве примера приведем отдельные фрагменты из тех сочинений, в которых дан неполный или неправильный ответ на некоторые вопросы:
" ... А что же такое планеты? Это звезды, ... они могут быть в несколько раз больше Земли ... . В одной из них (галактик - Е. К.) - галактике Солнца - расположена и наша Земля ... " . (Саша К.)
"… каждая звезда - планета. Одни звезды расположены ближе к нам - они изучены, другие настолько далеко, что их невозможно изучить. Известно, например, что на Луне и на Венере жизнь невозможна, а на Марсе под вопросом ... " (Лариса Б.)
" … В нашей галактике находится несколько планет, вращающихся вокруг Солнца. В нашей галактике жизнь существует лишь на нашей планете - Земле ..." (Лена Ч)
"… Мне кажется, что вся наша солнечная система вращается вокруг большей звезды, чем наше Солнце ..." (Люда М.).
Мы привели наиболее типичные ошибочные фрагменты из ответов учащихся. Как видно, наиболее часто встречаемая ошибка заключается в том, что ученики не понимают различия между планетой и звездой и отождествляют понятия Галактики и Солнечной системы. По сравнению с этими, другие ошибочные утверждения были более редкими, либо вообще носили исключительный характер. Гораздо чаще встречались очень неполные ответы, например:
"Во Вселенной расположены планеты и звезды. Они удалены на разные расстояния от Земли и от Солнца. Вращаются вокруг Солнца и вокруг оси. Полный оборот планеты вокруг своей оси считают годом. Звезды - это планеты больших или меньших размеров. На этих планетах, как и на нашей Земле есть горы и океаны". (Юра П.) .
Понятно, что такой ответ на поставленный вопрос нельзя считать удовлетворительным ни по объему, ни по качеству. Такое сильное различие знаний учащихся по данным вопросам можно объяснить большим интересом некоторых школьников к соответствующей научно-популярной литературе, кинофильмам, радио- и теле - передачам. Несмотря на очень широкий характер распространения информации такого рода далеко не все учащиеся получают её. Поэтому мы должны были сделать совершенно однозначный вывод:
Несмотря на то, что все обсуждаемые нами вопросы в той или иной степени объясняются на уроках обществоведения или географии, перед началом изучения курса астрономии и 10 -м классе учитель должен провести с учащимися вступительную беседу. В ней он сообщает и повторяет ранее полученные учащимися сведения о картинах мироздания, знание которых является не просто желательным, но совершенно необходимым для успешного понимания не только вводных, но и многих других вопросов курса астрономии в средней школе.
О целесообразности проведения беседы такого рода писал Е.П. Левитан, придя к такому выводу с несколько иных позиций: "…Чтобы важнейшие вопросы, касавшиеся устройства мира, были достаточно глубоко усвоены учащимися, желательно на первом урока в общих чертах дать учащимся представление о строении Вселенной, а все последующее изложение курса астрономии построить как доказательство справедливости сформулированных положений" [176, стр. 105].
1 С.Л. Рубинштейн.
Психологические воззрения И.М. Сеченова и
советская психологическая наука. "Материалы
совещания по психологии", М., АПР РСФСР, 1957 г.
2 Соображения, по которым
мы пришли к выражению именно такого
аналитического вида, совершенно аналогичны
проведенным ранее рассуждениям в отношении
окончательного вида аналитического
выражения величины "P" и поэтому здесь
не приводятся.
3 Стиль сочинения оставлен
нами без каких-либо изменений и исправлений.
| << Предыдущая |