 |
Астронет: Геологический факультет МГУ Геофизические методы исследования земной коры. Часть 1 http://www.astronet.ru/db/msg/1173309/page3.html |
Глава 1. Гравиразведка
- 1. Основы теории гравитационного поля Земли и гравиразведки
- 1.1. Сила тяжести, ее потенциал и производные потенциала
- 1.2. Нормальное значение силы тяжести, редукции, аномалии силы тяжести и плотность горных пород
- 1.2.1. Нормальное значение силы тяжести
- 1.2.2. Редукции силы тяжести
- 1.2.3. Аномалии силы тяжести
- 1.2.4. Плотность горных пород
- 1.3. Принципы решения прямых и обратных задач гравиразведки
- 1.3.1. Аналитические способы решения прямых задач гравиразведки
- 1.3.2. Прямая и обратная задачи над шаром
- 1.3.3. Прямая и обратная задачи над горизонтальным бесконечно длинным круговым цилиндром
- 1.3.4. Прямая и обратная задача над вертикальным уступом (сбросом)
- 1.3.5. Графическое определение аномалии силы тяжести двухмерных тел с помощью палетки Гамбурцева
- 1.3.6. Численные методы решения прямых и обратных задач гравиразведки
- 2. Аппаратура, методика и обработка данных гравиразведки
- 2.1. Принципы измерений силы тяжести и аппаратура для гравиразведки
- 2.1.1. Измеряемые в гравиразведке параметры
- 2.1.2. Динамические методы
- 2.1.3. Статистические гравиметры
- 2.1.4. Вариометры и градиентометры
- 2.2. Методика гравиметрических съемок
- 2.2.1. Общая характеристика методики гравиразведки
- 2.2.2. Наземная гравиметровая съемка
- 2.2.3. Обработка данных гравиметровых съемок
- 2.3. Методики других видов гравиразведки
- 3. Интерпретация и задачи, решаемые гравиразведкой
Гравиметрическая или гравитационная разведка (сокращенно гравиразведка) - это геофизический метод исследования земной коры и разведки полезных ископаемых, основанный на изучении распределения аномалий поля силы тяжести Земли вблизи земной поверхности, акваториях, в воздухе. Поле силы тяжести обусловлено в основном Ньютоновским притяжением Землей всех тел, обладающих массой. Так как Земля сферически неоднородна, да еще вращается, то поле силы тяжести на земной поверхности непостоянно. Изменения эти малы и требуют высоко-чувствительных приборов для их изучения. Основными измеряемыми параметрами гравитационного поля являются ускорение силы тяжести и градиенты (изменения ускорения по разным направлениям). Величины параметров поля силы тяжести зависят, с одной стороны, от причин, обусловленных притяжением и вращением Земли (нормальное поле), а с другой стороны - от неравномерности изменения плотности пород, слагающих земную кору (аномальное поле). Эти две основные причины изменения силы тяжести на Земле послужили основой двух направлений гравиметрии: геодезической гравиметрии и гравитационной разведки.
От других методов разведочной геофизики гравиразведка отличается сравнительно большой производительностью полевых наблюдений и возможностью изучать горизонтальную (латеральную) неоднородность Земли. Гравиразведка применяется для решения самых различных геологических задач с глубинностью исследований от нескольких метров (например, при разведке окрестностей горных выработок) до 200 километров (например, при изучении мантии).
1. Основы теории гравитационного поля Земли и гравиразведки
1.1. Сила тяжести, ее потенциал и производные потенциала
1.1.1. Сила тяжести.
Силой тяжести (![]() ) называют равнодействующую двух сил - силы ньютоновского
притяжения всей массой Земли (
) называют равнодействующую двух сил - силы ньютоновского
притяжения всей массой Земли (![]() ) и центробежной
силы, возникающей вследствие суточного вращения Земли (
) и центробежной
силы, возникающей вследствие суточного вращения Земли (![]() ).
Отнесенные к единице массы, эти силы характеризуются ускорениями
силы тяжести g=F/m, ньютоновского притяжения
f=Fн/m и центробежным P=P/m. Ускорение силы тяжести равно геометрической
сумме ускорения притяжения и центробежного ускорения (рис. 1.1).
Обычно в гравиметрии, когда говорят "сила тяжести", подразумевают
именно ускорение силы тяжести.
).
Отнесенные к единице массы, эти силы характеризуются ускорениями
силы тяжести g=F/m, ньютоновского притяжения
f=Fн/m и центробежным P=P/m. Ускорение силы тяжести равно геометрической
сумме ускорения притяжения и центробежного ускорения (рис. 1.1).
Обычно в гравиметрии, когда говорят "сила тяжести", подразумевают
именно ускорение силы тяжести.
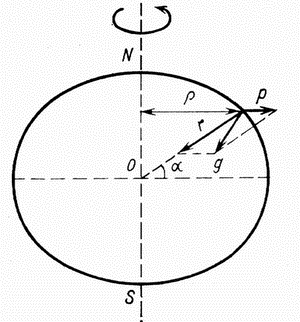 |
| Рис. 1.1 Ускорение силы тяжести и его составляющие |
Единицей ускорения в системе СИ является м/с2. В гравиметрии традиционно используют более мелкую единицу - Гал, равный 1 см/с2. В среднем на Земле g=981 Гал. В практике гравиразведки применяется величина в 1000 раз меньшая, получившая название миллигал (мГал).
Сила притяжения какой-либо
массы (![]() ) всей массой Земли (
) всей массой Земли (![]() ) определяется законом
всемирного тяготения Ньютона:
) определяется законом
всемирного тяготения Ньютона:
| (1.1) |
где
Центробежная сила (![]() ) направлена по радиусу,
перпендикулярному оси вращения (
) направлена по радиусу,
перпендикулярному оси вращения (![]() ), и определяется формулой
), и определяется формулой
| (1.2) |
где
Величина ![]() изменяется от нуля на полюсе
(R=0) до максимума на экваторе. Отношение
изменяется от нуля на полюсе
(R=0) до максимума на экваторе. Отношение ![]() , поэтому сила тяжести почти целиком определяется
силой притяжения, а ускорение силы тяжести практически равно ускорению
притяжения
, поэтому сила тяжести почти целиком определяется
силой притяжения, а ускорение силы тяжести практически равно ускорению
притяжения ![]() .
.
Земля в первом приближении является эллипсоидом
вращения, причем экваториальный радиус ![]() , а полярный
, а полярный ![]() , a-c=21 км. Разная величина радиуса Земли на полюсе и экваторе наряду
с изменением центробежной силы приводит к увеличению
, a-c=21 км. Разная величина радиуса Земли на полюсе и экваторе наряду
с изменением центробежной силы приводит к увеличению ![]() на
полюсе (gп=983 Гал) по сравнению с
на
полюсе (gп=983 Гал) по сравнению с ![]() на экваторе (gэ= 978 Гал). По известным
на экваторе (gэ= 978 Гал). По известным
![]() и
и ![]() были определены масса Земли М=5,98*1024 кг и ее средняя плотность
были определены масса Земли М=5,98*1024 кг и ее средняя плотность ![]() .
.
1.1.2. Потенциал силы тяжести.
Потенциал силы тяжести (![]() ) был введен в теорию
гравиметрии для облегчения решения теоретических задач. В точке А, расположенной на расстоянии rA от центра
Земли, выражение для потенциала принимается равным: WA=GM/rA, а в любой точке B, расположенной на продолжении радиуса
) был введен в теорию
гравиметрии для облегчения решения теоретических задач. В точке А, расположенной на расстоянии rA от центра
Земли, выражение для потенциала принимается равным: WA=GM/rA, а в любой точке B, расположенной на продолжении радиуса ![]() ,
, ![]() .
Поэтому разность потенциалов будет равна:
.
Поэтому разность потенциалов будет равна:
В пределе при малом
отсюда g=-dW/dr, т.е. сила тяжести есть производная потенциала силы тяжести по направлению к центру Земли.
С другой стороны, работа,
которая может быть произведена при движении притягиваемой точки
по отрезку ![]() , равна
, равна ![]() . Поэтому
. Поэтому ![]() , или работа
силы тяжести по перемещению единичной массы на отрезке
, или работа
силы тяжести по перемещению единичной массы на отрезке ![]() равна разности значений потенциала на концах этого отрезка.
равна разности значений потенциала на концах этого отрезка.
При перемещении точки в направлении, перпендикулярном силе тяжести, dW=0. Это означает, что W=const. Поэтому гравитационное поле можно представить в виде набора бесконечного числа поверхностей, на которых потенциал остается постоянным, а ускорение силы тяжести направлено перпендикулярно этой поверхности. Такие поверхности называют эквипотенциальными или уровенными. В частности, поверхность жидкости на Земле, например, моря, совпадает с уровенной поверхностью. У Земли есть одна уникальная уровенная поверхность, которая совпадает с невозмущенной волнениями поверхностью океанов. Она называется геоидом.
Таким образом, геоид - это условная уровенная поверхность, которая совпадает со средним уровнем океанов и открытых морей, проходит под сушей и по определению везде горизонтальна, а ускорение силы тяжести к ней перпендикулярно.
1.1.3. Производные потенциала силы тяжести.
Производные потенциала силы тяжести по трем координатным
осям ![]() ,
, ![]() ,
, ![]() однозначно определяют его полный вектор.
однозначно определяют его полный вектор.
В частности, если ось z направить к центру Земли, то ![]() , а
, а ![]()
В гравиметрии кроме первых производных изучаются
вторые производные потенциала или их разности:
| (1.3) |
Физический смысл этих выражений легко получить, если иметь в виду, что
Аналогичный смысл имеют вторые производные ![]() и
и ![]() .
.
Вторые производные ![]() ,
, ![]() характеризуют форму уровенной поверхности
(геоида), изучаемую в геодезической гравиметрии. Практической единицей
измерения градиента силы тяжести принимается 1 этвеш (Е)=10-9/c2, что соответствует изменению силы тяжести
в 0,1 мГал на 1 км.
характеризуют форму уровенной поверхности
(геоида), изучаемую в геодезической гравиметрии. Практической единицей
измерения градиента силы тяжести принимается 1 этвеш (Е)=10-9/c2, что соответствует изменению силы тяжести
в 0,1 мГал на 1 км.