Астронет > Горячие "черные дыры". Новое в понимании природы теплоты

Астронет: Д. А. Киржниц/СОЖ Горячие "черные дыры". Новое в понимании природы теплоты
http://variable-stars.ru/db/msg/1171229/kirzhnits.html

Горячие "черные дыры". Новое в понимании природы теплоты

Д.А.КИРЖНИЦ

Московский государственный университет им. М.В. Ломоносова

Дается краткий научно-популярный обзор одного из крупнейших достижений астрофизики последних двух десятилетий - создания термодинамики гипотетических небесных объектов "черных дыр", которая описывает их необычные тепловые свойства. Общеизвестный механизм появления тепла - хаотическое движение частиц нагретого тела - оказывается далеко не единственным.

Современная наука знает, что пресе- чение информации есть путь энтро- пии, всеобщего разрушения и xaoca ...
	А.И. Солженицын. Нобелевская лекция

Среди великого многообразия небесных тел особое место занимает класс объектов, называемых черными дырами (ЧД). Их поле тяготения столь велико, что никакая частица, включая частицу (квант) света, не может вырваться изнутри такого объекта и уйти на бесконечность. Поэтому его поверхность действует как своего рода клапан, пропускающий вещество лишь в одну сторону - внутрь ЧД (отсюда и это название: вещество валится в ЧД как в дыру, а свет из нее выйти не в состоянии). Это уникальное свойство ЧД прямо ведет к удивительному факту - внешнему наблюдателю она представляется как горячее тело, служащее источником теплового излучения. Это и другие тепловые свойства ЧД описываются специальной теорией - термодинамикой черных дыр, краткий очерк которой и составляет содержание статьи.

1. Черные дыры

Небесные тела со свойствами ЧД рассматривались в рамках механики Ньютона еще в XVIII веке как объекты, вторая космическая скорость которых (необходимая, чтобы любое тело покинуло их поверхность и ушло на бесконечность) $\upsilon_2 = \sqrt{2GM/R}$ превышает скорость света c = 3 $\cdot$ 10¹⁰ см/с. Здесь G = 6,7 $\cdot$ 10^{- 8} эрг $\cdot$ см/г² - постоянная тяготения, М - масса объекта, R - его радиус. Приведенному условию удовлетворяет объект, масса которого сконцентрирована в очень малом объеме с радиусом

$R\leq r_g = 2GM / c^{2}\simeq 3\left(M/M_{\odot}\right)~\textrm{км,}$

(1)

где $r_g$ - так называемый гравитационный радиус тела, $M_{\odot}$ = 2 $\cdot$ 10³³ г - масса Солнца. Сферу радиуса $r_g$ называют горизонтом событий: именно ею ограничено поле зрения внешнего наблюдателя, лишенного информации о ее внутренней части. Условие (1) оказалось справедливым и в рамках общей теории относительности.

Для подавляющей части небесных тел это условие резко нарушено. Так, для Солнца (радиус 7 $\cdot$ 10⁵ км) и Земли (масса 6 $\cdot$ 10²⁷ г, радиус 6 $\cdot$ 10³ км) величина r_g составляет соответственно всего 3 км и 1 см. Еще контрастнее соответствующие цифры для "земных" объектов. Поэтому ЧД возникает лишь при крайне необычных условиях сверхвысокой плотности вещества. Такие условия имеются прежде всего на конечном этапе эволюции звезд с массой, превышающей примерно 3 $M_{\odot}$ : неудержимое гравитационное сжатие такой звезды - коллапс ведет в конечном счете к выполнению условия и (1) образованию звездной ЧД. Масса таких объектов лежит в диапазоне от 3 до 100 $M_{\odot}$ . Более тяжелые массивные и сверхмассивные ЧД с массами до 10⁸ $M_{\odot}$ возникают в результате коллапса больших масс газа в центре шаровых скоплений, ядрах галактик и квазарах. Легкие же ЧД с массами до 3 $M_{\odot}$ могли бы образоваться в результате нарастания флуктуаций плотности сверхсжатого вещества ранней Вселенной (первичные ЧД).

Абсолютно твердых доказательств существования ЧД в космосе пока нет. Однако большинство ученых сходятся на том, что рентгеновские источники в некоторых двойных системах представляют собой звездные ЧД, а активность многих (если не всех) ядер галактик и квазаров - результат существования массивных и сверхмассивных ЧД в центрах этих объектов.

Предшественник ЧД (массивная звезда, газ, флуктуация плотности) обладает множеством наблюдаемых параметров, относящихся как к его глобальным свойствам, так и к характеристикам ее внутреннего строения. Информация о подавляющей части таких параметров теряется внешним наблюдателем в процессе образования ЧД, которая, как уже подчеркивалось, не выпускает изнутри себя никаких сигналов, характеризующих состав и структуру вещества, распределение электрических токов и др. Этот факт образно описывают словами "ЧД не имеет волос". Фактически наблюдатель может измерить лишь такие глобальные характеристики ЧД, как ее масса М, вращательный момент и полный электрический заряд Q.

2. Эффект Хокинга

Нарисованная выше картина ЧД имеет классический, неквантовый характер. Квантовая механика вносит в нее некоторые коррективы: при сохранении горизонта событий ЧД перестает быть "черной", становясь источником излучения. Оно имеет ту же природу, что и электрон-позитронные пары, рождаемые сильным электрическим полем, которое увеличивает энергию виртуальных (короткоживущих) пар в вакууме, превращая их в реальные (долгоживущие). Аналогично рождает пары (в том числе и пары фотонов) и сильное поле тяготения ЧД, действующее на частицы любого сорта. Один из компонентов пары становится реальной частицей снаружи (и вблизи) горизонта событий и, имея положительную энергию, может уйти на бесконечность, другая появляется внутри (и вблизи) горизонта и падает с отрицательной энергией внутрь ЧД (рис. 1).

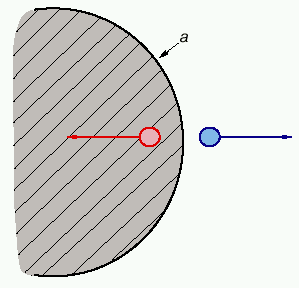Рис. 1. Рождение пар частиц в поле черной дыры. а - горизонт событий. Заштрихована черная дыра

В итоге ЧД становится источником непрерывного потока частиц, уходящего на бесконечность. Подчеркнем, что при формировании такого излучения никакая частица не пересекает горизонта событий, который тем самым по-прежнему обладает свойствами клапана.

В 1974-1975 годах английский теоретик С. Хокинг проводил вычисления характеристик излучения ЧД, руководствуясь нарисованной выше физической картиной. К своему удивлению он обнаружил, что свойства такого излучения в точности такие же, как у излучения горячего черного тела радиуса r_g , нагретого до температуры

$kT\simeq 0,5\cdot 10^{-7}\left(M_{\odot} / M\right)~\mathrm{K},$

(2)

где $k = 1,4 \cdot 10^{-16}$ эрг/К - постоянная Больцмана. Примечательно, что в описанном явлении, которое называют эффектом Хокинга, температура обратно пропорциональна массе. В процессе излучения масса ЧД уменьшается, а ее температура растет, что усиливает излучение и тем самым ускоряет убыль массы. Поэтому со временем ЧД "разгорается", ее температура быстро растет и за конечное время

$\tau\approx 10^{72}\,\left(M_{\odot} / M\right)^{3}~\textrm{секунд}$

(3)

ЧД прекращает существование, исчерпав свою массу.

Существенно, что последние мгновения перед исчезновением ЧД будут протекать в режиме мощного взрыва с выделением энергии порядка 10³⁰ эрг за время порядка 0,1 с. Такие взрывы можно было бы наблюдать и на большом удалении от Земли. Впрочем, это не относится к звездным и тем более массивным и сверхмассивным ЧД: уже при $(M_{\odot} / M)$ температура составляет ничтожные доли градуса, а время жизни ЧД намного больше времени существования Вселенной (см. (2),(3)). Поэтому взрываться в нашу эпоху способны лишь первичные ЧД с массой порядка 10¹⁵ г (масса средней горы). К сожалению, такие взрывы до сих пор не наблюдались.

Как ни впечатляющи следствия эффекта Хокинга, в теоретическом плане наибольший интерес представляет природа теплового характера ЧД: имеем ли мы здесь дело с чисто случайным сходством или же по каким-то причинам ЧД действительно представляет собой горячее тело? Ответ на этот вопрос и служит содержанием оставшейся части статьи.

3. Термодинамика черных дыр

После открытия эффекта Хокинга научное общественное мнение склонялось скорее к тому, что имеет место чисто внешняя аналогия с термодинамическими соотношениями. Ведь ни в самой постановке задачи об излучении ЧД, ни в чисто динамическом методе ее решения нет, казалось бы, ни малейшего намека на термодинамику. Однако такая точка зрения просуществовала недолго. Пришлось вспомнить, что еще до открытия Хокинга высказывалось немало соображений, свидетельствующих о тесном переплетении физики ЧД и термодинамики.

Все началось, по-видимому, с задачи, которую поставил известный американский теоретик Дж. Уилер перед своим аспирантом Дж. Бекенштейном за несколько лет до работ Хокинга. Пусть первоначально имеются ЧД и вдали от нее горячее тело, обладающее некоторым запасом энтропии. Эта величина, о которой упоминается в эпиграфе статьи, представляет собой меру того хаоса, который мы связываем с понятием теплоты (о количественном определении энтропии см. ниже раздел 5). ЧД притянет к себе тело, которое в конце концов уйдет под горизонт событий. Тогда наблюдатель столкнется с явным нарушением второго начала термодинамики, согласно которому полная энтропия замкнутой системы (в данном случае системы ЧД + тело) не может уменьшаться со временем - порядок в отличие от хаоса не может возникать сам собой. Ведь в начале энтропия системы равнялась энтропии тела, а в конце она исчезла, так как внутренность ЧД наблюдателю недоступна. На это хочется возразить, что на самом деле энтропия тела не исчезла, а передалась внутренней части ЧД. Но этот аргумент не более чем отговорка: физический мир внешнего наблюдателя не включает в себя внутренности ЧД, а общие законы физики должны выполняться именно в этом мире.

Существовали и другие, более формальные свидетельства того, что в физике ЧД, так сказать, "пахнет" термодинамикой. Например, как показал сам Хокинг, поверхность ЧД (для нескольких ЧД - сумма поверхностей)

$F=4\pi r_{g}^2$

(4)

ведет себя подобно энтропии, не уменьшаясь ни при каких естественных процессах с участием ЧД - при падении вещества в ЧД, при слиянии двух ЧД в одну и т.п. (в этом легко убедиться с помощью соотношений (1), (4)). Однако до поры до времени такие свидетельства воспринимались как проявление чисто формальной аналогии.

По-видимому, только Бекенштейн почувствовал, что за всем сказанным стоит глубокая физика. Отвергнув возможность нарушения второго начала, он дал следующее решение задачи Уилера. При падении тела внутрь ЧД такие его характеристики, как масса, вращательный момент и заряд, не исчезают, а передаются ЧД как целому, меняя соответствующим образом значения ее наблюдаемых параметров $М,\overrightarrow{m}, Q$ (см. конец раздела 1). Бекенштейн расширил список таких характеристик тела, включив в него и энтропию, одновременно введя ее и в список наблюдаемых параметров ЧД. Спасение второго начала происходит при этом потому, что падающее тело меняет (увеличивает) энтропию самой ЧД на величину, не меньшую исходной энтропии тела.

Но Бекенштейн на этом не остановился, всерьез восприняв ЧД как термодинамический объект. Он определил температуру ЧД (она практически совпала с результатом Хокинга, см. (2)), придумав особого рода машину, которая способна (мысленно, конечно) превращать тепло в работу в поле ЧД (грубо говоря, это заполненный горячим излучением контейнер на длинной нити, который после его спуска до горизонта событий опорожняется, потом поднимается обратно уже в облегченном виде; выигрыш в энергии при спуске поэтому не меньше ее затрат при подъеме, рис. 2).

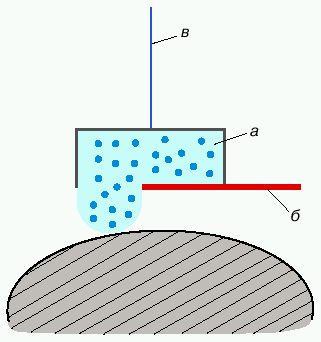Рис. 2. Тепловая машина Бекенштейна: а - контейнер с горячим излучением, б - заслонка, в - нить

Температура ЧД определяется коэффициентом полезного действия такой машины (теорема Карно). Одновременно, используя (4) , Бекенштейн нашел и энтропию ЧД, оказавшуюся пропорциональной ее поверхности.

$S \approx k\cdot 10^{75}\,\left(M_{\odot} / M\right)^{2}\propto F\,.$

(5)

Этот факт снимает покров таинственности со сказанного выше о свойствах поверхности ЧД, оказывающихся прямым следствием второго начала термодинамики.

Определив температуру и энтропию ЧД, Бекенштейн, однако, не сделал последнего шага - не предсказал самого эффекта Хокинга, который по справедливости должен был бы носить имя обоих ученых.

4. Коллапс тел малой массы

Выводом о неравенстве нулю температуры ЧД (и тем самым о существовании эффекта Хокинга) результаты термодинамики ЧД далеко не ограничиваются. Эта теория, как и любой другой раздел термодинамики, позволяет делать общие и достаточно сильные утверждения без проведения конкретных микроскопических расчетов. Еще один пример такого рода приводится в этом разделе.

Выше уже говорилось, что коллапс могут испытывать лишь тела с массой, превышающей примерно $3M_{\odot}$ . В 1962 году советский теоретик Я.Б. Зельдович показал, что такая граница относится лишь к быстрому коллапсу. В действительности неудержимо сжиматься, хотя и чрезвычайно медленно, способно тело произвольно малой массы - состояние ЧД энергетически предпочтительно при любом значении М.

Термодинамика ЧД вносит существенные коррективы в этот вывод. Применим к процессу коллапса второе начало термодинамики, требующее, чтобы энтропия исходного состояния была не больше энтропии возникающего из него состояния ЧД. Первую из этих величин можно оценить, считая, что на каждую степень свободы классической системы частиц приходится энтропия порядка постоянной Больцмана

$S \sim kM\cdot 10^{57}\,\left(M_{\odot}/M\right)\,,$

(6)

где m = 1,6 $\cdot$ 10^-24 г - масса нуклона. Вторая величина дается формулой (5) . Отсюда прежде всего видно, что процесс коллапса с образованием звездной ЧД сильно необратим: энтропия в итоге такого процесса возрастает почти на 20 порядков для $М ~ M_{\odot}$ .

Будем теперь уменьшать массу М. При этом, как видно из формул (5), (6),<энтропия ЧД будет уменьшаться быстрее энтропии исходного тела и при значении М ~ 10¹⁵ г эти величины становятся равными друг другу. При дальнейшем уменьшении М энтропия в процессе коллапса должна была бы уменьшиться, что противоречит второму началу термодинамики. Таким образом, нижняя граница массы коллапсирующего тела хотя и смещается вниз по отношению к величине 3 $M_{\odot}$ , но остается отличной от нуля. Подчеркнем, что приведенные рассуждения относились лишь к коллапсу изолированного тела и никоим образом неприложимы к первичным ЧД (см. раздел 1).

5. Термодинамика и информация

Существование области, информация из которой не доходит до наблюдателя, имеет для термодинамики ЧД принципиальное значение. Это видно уже из формулировки задачи Уилера, описанной в разделе 3, разделе 3, которая послужила отправным пунктом аргументации Бекенштейна. В более общем плане это ясно из следующих квантовомеханических соображений. Горячая ЧД, как и любое горячее тело, должна описываться не волновой функцией, а особой величиной - матрицей плотности, которая осуществляет неполное описание системы. Такая неполнота в случае обычного горячего тела связана с невозможностью детального описания составляющих его частиц, в случае ЧД как динамической системы - с существованием указанной выше области.

Существует достойная особого внимания возможность прямого перехода от утверждения "наблюдатель не имеет информации о внутренней части ЧД" к утверждению "ЧД обладает запасом энтропии, а значит, и отличной от нуля температурой". Эта возможность опирается на сформулированный американским физиком Л. Сциллардом особый информационный подход к термодинамике, который восходит к классикам теории теплоты и развивался многими физиками и математиками. Такой подход по сути сводится к установлению прямой связи величины энтропии системы с недостатком информации о ее внутренней структуре. Сразу же подчеркнем, что речь идет об объективном, принципиально невосполнимом недостатке информации, а не просто об отказе от возможной в принципе регистрации характеристик системы.

Идею информационного подхода сформулируем сначала на примере обычной термодинамики, точнее говоря, на примере перехода динамической системы в состояние термодинамического равновесия. Будем опираться на реальный пример - метод получения высокотемпературной плазмы путем инжекции в специальную камеру сгустка ускоренных частиц с его последующей термализацией. Первоначальный сгусток - для определенности монохроматический и поляризованный - представляет собой динамическую систему, описываемую волновой функцией. В процессе нелинейного взаимодействия частиц сгустка в камере и развития соответствующих неустойчивостей система частиц хаотизуется и переходит в термодинамически равновесное состояние, описываемое матрицей плотности, причем соответствующая температура определяется первоначальной энергией сгустка. В итоге система "забывает" свое начальное состояние, характеризуясь существенно меньшим числом параметров (энергия или температура, давление или объем и т.п.), чем полное число ее степеней свободы. Существенно, что каждому набору таких параметров отвечает огромное число N различных микросостояний системы - комплексий по терминологии Больцмана, которые реализуют этот набор и которые мы в принципе не можем различать. Равновероятность различных комплексий, невозможность предпочесть одну из них другой и есть точный и наиболее общий смысл понятия "хаос".

Число комплексий N определяет по существу степень неполноты наших сведений о микроструктуре системы при заданном наборе указанных макроскопических параметров. Более удобной мерой такой неполноты информации о системе служит уже многократно упомянутая выше энтропия системы, определяемая соотношением

$S = k \ln N$

(7)

и измеряемая в единицах постоянной Больцмана (см. формулу (5)). Мы подошли, таким образом, к информационному толкованию энтропии.

Чтобы дать такому толкованию количественную формулировку, введем следующее простейшее определение изменения количества информации $\Delta I$ в результате некоторого процесса. Пусть до его начала имелось P равновероятных ответов на некоторый вопрос о рассматриваемой системе, ни один из которых нельзя предпочесть другому. Пусть по окончании процесса число таких ответов стало p. Тогда изменение информации о системе имеет вид

$\Delta I = k\ln(P/p)$ .

Если P > p, то имеется прирост информации $\Delta I$ > 0 - наши сведения о системе стали более определенными, а в обратном случае - ее убыль.

Приложим такое определение к рассмотренному выше процессу перехода системы в термодинамически равновесное состояние. Вначале она была чисто динамической, ее энтропия равнялась нулю, и мы знали единственный ответ на вопрос о ее микросостоянии: P = 1. В конце энтропия системы увеличилась на величину $\Delta S$ , а число ответов на поставленный вопрос выросло до p = N. Поэтому убыль информации после термализации равна $\Delta I = k\ln N$ , и мы пришли к основному соотношению информационного подхода (см. (7))

$\Delta S=-\Delta I\,,$

(8)

то есть уменьшение количества информации о системе равно приросту ее энтропии и обратно. Важно, что при выводе (8) не использовался никакой конкретный механизм потери информации, что побуждает считать это соотношение универсальным.

Проиллюстрируем соотношение (8) простым примером необратимого расширения на весь объем газа, первоначально сосредоточенного в половине объема (рис. 3).

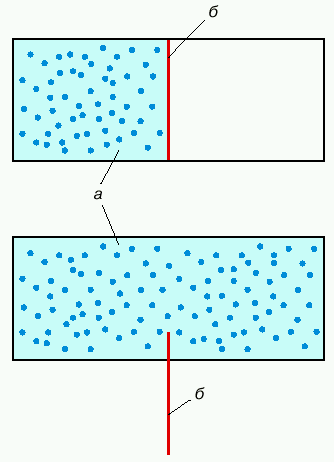Рис. 3. Расширение газа в удвоенный объем. а) - газ, б) - заслонка

Очевидно, что число равновероятных ответов на вопрос о поперечной по отношению к заслонке координате молекулы газа увеличивается после поднятия заслонки вдвое. Соответствующая убыль информации равна kln 2, что в соответствии с (8) точно равно известному из термодинамики выражению для приходящегося на одну молекулу прироста энтропии в рассматриваемом процессе.

Важно подчеркнуть, что из соотношения (8) никоим образом не следует возможность нарушить второе начало термодинамики, то есть уменьшить энтропию замкнутой системы путем увеличения объема информации о ней. Дело в том, что за получение информации надо платить определенную цену, в том числе энтропийную, поскольку сам этот процесс необратим. Так, например, при определении координаты молекулы путем ее освещения придется считаться с тем, что рассеянный молекулой свет в конце концов диссипирует, поглотится системой, повысив ее энтропию на величину, не меньшую выигрыша за счет соотношения (8). Самое большее, чего можно достичь, - это перераспределить энтропию (степень хаотичности) с одних степеней свободы на другие. Именно к этому и сводится работа технических устройств, упорядочивающих систему по некоторым параметрам, - регуляторов, которые обязательно имеют специальный орган (датчик), считывающий информацию о регулируемой величине.

Перейдем, наконец, к изложению информационного подхода применительно к процессу образования ЧД. Ситуация здесь очень близка к рассмотренному примеру термализации сгустка (от несущественной разницы - возможности ненулевой температуры у предшественника ЧД - можно отвлечься). Как было отмечено в конце раздела 1, и в случае ЧД нам был доступен огромный объем информации о микросостоянии ее предшественника, "забытый" в процессе образования ЧД, которая помнит лишь малое число наблюдаемых параметров. Поэтому применительно к образованию ЧД можно повторить почти все сказанное выше. Во всяком случае сам факт обладания ЧД отличной от нуля энтропией нужно считать естественным и неизбежным.

Остается, однако, количественная проблема доказательства совпадения информационной (см. (7) или (8)) и термодинамической (см. (6)) формул для энтропии. Для этого нужно прежде всего выявить те микросостояния, информации о которых лишен внешний наблюдатель. Уже из факта сильной необратимости процесса образования звездной ЧД (см. раздел 4) следует, что они не связаны со степенями свободы предшественника ЧД. Этот вопрос оказался далеко не простым, поэтому решение обсуждаемой проблемы затянулось на долгие годы. Такое решение было предложено лишь в самое последнее время. Исследования сотрудников Физического института им. П.Н. Лебедева РАН, российских теоретиков И.Д.Новикова и В.П.Фролова показали, что микросостояния, играющие роль комплексий Больцмана (см. раздел 5), связаны с компонентами пар, которые рождены около горизонта событий (рис. 1), падающими внутрь ЧД. Подсчет их вклада в энтропию ЧД ведет к формуле (5).

6. Некоторые другие примеры

Утверждение об универсальной связи (8) изменений энтропии и информации подкрепим двумя указанными канадским физиком У. Унру примерами, не относящимися к физике ЧД. Первый из них можно считать газодинамическим аналогом ЧД. Рассмотрим объем газа высокого давления, окруженный звукопоглощающей стенкой с отверстием, сквозь которое вырывается газ со сверхзвуковой скоростью, приобретаемой, например, при протекании через сопло Лаваля (рис. 4). В рамках газодинамики (от оптических явлений мы отвлекаемся) срез сопла можно считать горизонтом событий: никакой звуковой сигнал не может проникнуть снаружи внутрь объема. Согласно информационному подходу, наша система должна обладать запасом энтропии. И действительно, квантовый расчет звукового поля около отверстия показывает, что оно служит источником фононов, находящихся в состоянии термодинамического равновесия с некоторой отличной от нуля температурой.

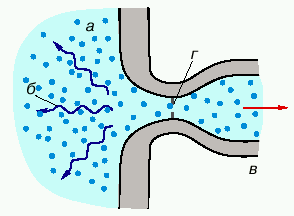Рис. 4. Газодинамическое устройство Унру: а - газ, б - звук, в - сопло Лаваля, г - его сверхзвуковой срез, играющий роль горизонта событий

Второй пример более сложен. Хорошо известно, что явления в поле тяготения и ускоренной системе отсчета имеют очень близкую и глубокую аналогию, которая подсказала Эйнштейну путь к созданию общей теории относительности. Проявлением такой аналогии служит, например, невесомость в орбитальном полете: тяготение и центробежная сила точно компенсируют друг друга. Поэтому можно ожидать, что силу тяготения как причину эффекта Хокинга можно заменить переходом к ускоренной системе отсчета, движущейся с ускорением a. И в самом деле расчет показывает, что равномерно ускоренный в вакууме наблюдатель увидит тепловое излучение, отвечающее температуре

$kT\propto a$ .

Для пояснения отметим без доказательства, что и в рассматриваемом случае имеется горизонт событий: существует область пространства-времени, для которой испущенный из нее свет никогда не догонит ускоренного наблюдателя. К тому же в вакууме всегда есть физические короткоживущие поля (нулевые колебания), которые не регистрируются обычным, движущимся инерциально прибором, настроенным на эти колебания как на "нуль" (начало отсчета). Тот же прибор, движущийся ускоренно, зарегистрирует такие колебания как тепловое излучение.

7. Заключение

Существование ЧД, предсказанных в их современном понимании общей теорией относительности, с большой долей вероятности уже подтверждено наблюдениями (см. раздел 1). Если эта вероятность превратится в полную уверенность, то уже роль ЧД как источников активности ядер галактик и квазаров позволит считать их важнейшим элементом мироздания. Не исключено, что еще не открытые первичные ЧД, если они действительно существуют, имеют куда большую значимость для космофизики, чем это кажется сегодня.

Однако уже сейчас можно говорить и о совсем иной, общефизической роли ЧД, обогативших наши общие представления о неорганическом мире. Появление ЧД как продукта теоретической мысли подняло на новый уровень понимание теплоты. С XVIII-XIX веков - времени победы кинетической теории над теорией теплорода - наука знала единственный механизм появления тепла - хаотизацию движения частиц, обладающих запасом кинетической энергии. Такой механизм проявляется и при трении двух кусков дерева, с помощью чего наши предки добывали огонь, и при химических и ядерных реакциях. С наиболее общей, информационной точки зрения появление тепла во всех таких случаях отвечает утрате микроскопической информации о состоянии частиц горячего тела.

Физика ЧД указала новый механизм возникновения тепла, когда информация о внутреннем состоянии ЧД отсекается от наблюдателя мощными силами тяготения (а сам этот объект может быть уподоблен "черному ящику", как в кибернетике называют устройство с неизвестной внутренней структурой). Этот новый механизм действует по схеме

черная дыра $\rightarrow$ черный ящик $\rightarrow$ черное тело

и также имеет дело с хаосом, которому отвечает равновероятность с точки зрения внешнего наблюдателя различных микросостояний внутренней части ЧД, совместимых с заданными значениями массы, момента и заряда (см. раздел 5, конец третьего абзаца).

Сказанному точно соответствуют слова великого русского писателя, физика по образованию, взятые эпиграфом к статье (хотя сам он, конечно, вкладывал в них совсем иной, общественно-политический смысл).

Литература


[1]	Новиков И.Д., Фролов В.П. Физика черных дыр. М.: Наука, 1986.
[2]	Киржниц Д.А., Фролов В.П. // Природа. 1981. No 11. С. 2.
[3]	Киржниц Д.А., Фролов В.П. // Прошлое и будущее Вселенной. М.: Наука, 1986. С. 61.
[4]	Бриллюен Л. Наука и теория информации. М.: Физматгиз, 1960.
[5]	Hawking S. // Sci. Amer. 1977. Vol. 236, No 1. P. 34.
[6]	Bekenstein J. // Phys. Today. 1980. No 1. P. 24.