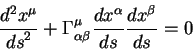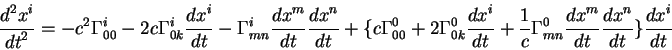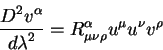Астронет > 8. Уравнение движения в общей теории относительности

Астронет: М. В. Сажин/ГАИШ Теория относительности для астрономов
http://variable-stars.ru/db/msg/1170927/node9.html

Теория относительности для астрономов

<< 7. Тензор кривизны | Оглавление | 9. Уравнения гравитационного поля >>

Разделы

8. Уравнение движения в общей теории относительности

Влияние гравитационного поля на движение частиц в ньютоновской механике хорошо изучено. Уравнение движения частицы представляет собой уравнение в левой части которого стоит ускорение пробной частицы умноженное на массу частицы (в данном случае это инертная масса), в правой части уравнения стоит гравитационная сила. Гравитационная сила, в свою очередь, представляет из себя произведение массы пробной частицы (в данном случае - гравитационной массы) на ускорение со стороны тяготеющего тела: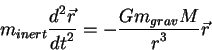

$\begin{displaymath} m_{inert}{\displaystyle d^2 \vec r\over\displaystyle dt^2}= -{\displaystyle Gm_{grav}M\over\displaystyle r^3} \vec r \end{displaymath}$

Поскольку инертная масса тела равна его гравитационной массе (это формулировка принципа эквивалентности, многократно проверенного экспериментально), то движение пробной частицы не зависит от массы этой частицы - перо птицы и кирпич падают в гравитационном поле с одинаковым ускорением (конечно, если пренебречь сопротивлением воздуха).

В общей теории относительности роль гравитационной силы играет кривизна пространства - времени. Движение в гравитационном поле - это движение в искривленном пространстве, отклонение от движения по прямой линии - это отклонение в движении возникающее в искривленном пространстве времени.

Вспомним вначале уравнения движения в специальной теории относительности.

8.1 Уравнение движения пробной частицы в СТО

В специальной теории относительности уравнение движения пробной частицы имеет вид:

$\begin{displaymath} m_{inert}c^2{\displaystyle d u^{\alpha}\over\displaystyle ds}=F^{\alpha}, \end{displaymath}$

(8.1)

где $u^{\alpha}$ - 4 скорость частицы (физическое определение) или вектор, касательный к траектории частицы (математическое определение). Отметим, что $u^{\alpha}$ - величина безразмерная, а имеет размерность [см]. Другими словами, слева стоит величина, которая имеет размерность силы г $\cdot{\displaystyle\mbox{см}\over\displaystyle\mbox{сек}^2}$ .

Уравнения движения электрона в электромагнитном поле имеют вид:

$\begin{displaymath} m_e c^2 {\displaystyle d u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath}$

(8.2)

Сила, которая стоит в левой части уравнения является 4 инвариантной силой Лоренца, построенной из тензора Максвелла $F^{\alpha \beta}$ .

В случае, когда действующие силы равны нулю $F^{\alpha}=0$ , то движение частицы происходит по инерции. Тогда решение уравнения 8.1 имеет тривиальный вид:

$\displaystyle u^{\alpha}(s)= u^{\alpha}_0$			(8.3)
$\displaystyle x^{\alpha}(s) = u^{\alpha} \cdot s +x^{\alpha}_0$			(8.4)

Движение по инерции - это движение по прямой линии. Прямая линия является линией кратчайшей длины между двумя точками в эвклидовой и псевдоэвклидовой геометрии. В неэвклидовой геометрии линия кратчайшей длины называется геодезической линией. Движение в случае, когда внешние силы равны нулю, в неэвклидовой геометрии заменяется общековариантным уравнением - движением по геодезической линии.

Отметим также, что решение (8.3) описывает также движение фотона, если полагать, что $u^{\alpha}$ - единичный вектор в направлении распространения фотона, а - афинный параметр вдоль траектории.

8.2 Уравнение движения пробной частицы в ОТО

Движение по геодезической линии описывает движение пробной частицы в гравитационном поле. Это движение является аналогом движения по инерции в пространстве с эвклидовой метрикой.

Выпишем уравнение движения в общей теории относительности, просто написав ковариантное обобщение уравнения 8.1:

$\begin{displaymath} m_{inert}c^2{\displaystyle D u^{\mu}\over\displaystyle ds}=F^{\mu} \end{displaymath}$

(8.5)

Здесь , как мы договорились выше, являются обозначением ковариантного дифференциала. Поэтому уравнения движения в общей теории относительности можно написать более детально в виде:

$\begin{displaymath} m_{inert}c^2{\displaystyle d u^{\mu}\over\displaystyle ds} +... ...c^2 \Gamma^{\mu}_{\alpha \beta} u^{\alpha} u^{\beta}=F^{\mu} \end{displaymath}$

(8.6)

Заметим, что теперь уравнения движения являются нелинейными (по скоростям), второй член в левой части уравнений содержит квадратичные произведения скоростей.

Теперь уравнения движения, например, электрона в электромагнитном поле имеют вид:

$\begin{displaymath} m_e c^2 {\displaystyle D u^{\alpha}\over\displaystyle ds}=e F^{\alpha \beta} u_{\beta} \end{displaymath}$

(8.7)

Здесь $F^{\alpha \beta}$ - тензор электромагнитного поля, а и масса и заряд электрона соответственно.

Отметим, что теперь движение пробной частицы в отсутствии внешних сил $F^{\alpha}=0$ уже не является движением по прямым линиям, как это было в эвклидовой геометрии (8.3). Движение в отсутствии внешних сил представляет из себя систему дифференциальных уравнений второго порядка для всех четырех координат, которые описывают четырехмерную траекторию пробной частицы.

8.2.1 Уравнения движения в трехмерном виде

Рассмотрим уравнения движения пробных частиц, написанные в трехмерном виде. Будем считать, что частица является нерелятивистской (т.е. интервал между двумя событиями: выходом частицы из точки и появление частицы в точке не равен нулю). Уравнения движения пробных частиц - уравнения геодезических линий имеют вид (8.6). В качестве афинного параметра вдоль геодезической возмем - интервал между событиями (т.к. он не равен нулю). Кроме того, напомним, что 4 скорость - это единичный вектор касательный к траектории движения, по определению:

$\begin{displaymath} u^{\alpha}={\displaystyle d x^{\alpha}\over\displaystyle d s} \end{displaymath}$

Это значит, что уравнения движения можно переписать в виде, который содержит ускорения (вторую производную от координаты частицы по афинному параметру):

$\begin{displaymath} {\displaystyle d^2 x^{\mu}\over\displaystyle ds^2} + \Gamma^... ...style ds} {\displaystyle d x^{\beta}\over\displaystyle d s}= 0 \end{displaymath}$

(8.8)

Преобразуем вторую производную от координаты с пространственным индексом по интервалу к второй производной по координате с нулевым индексом:

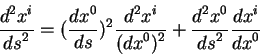
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2}=({\displayst... ...splaystyle ds^2} {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

Здесь $d x^0\over\displaystyle d s$ - нулевая компонента 4 скорости, а $d^2 x^0\over\displaystyle ds^2$ - 4 мерное уравнение движения с индексом 0.

Это уравнение можно обратить, получая уравнения для ускорений пробной частицы в виде:

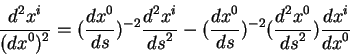
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = ({\disp... ...ystyle d s^2}) {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

Подставим в это уравнение выражение для

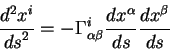
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d s^2} = - \Gamma^i... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}$

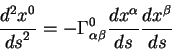
$\begin{displaymath} {\displaystyle d^2 x^0\over\displaystyle d s^2} = - \Gamma^0... ...style d s} {\displaystyle d x^{\beta}\over\displaystyle d s} \end{displaymath}$

После завершения всех выкладок, окончательно получаем уравнение движения в виде:

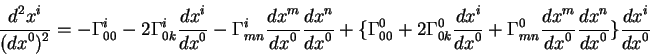
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle(d x^0)^2} = -\Gamma... ...e d x^0}\rbrace {\displaystyle d x^i\over\displaystyle d x^0} \end{displaymath}$

До сих пор дифференцирование проводилось по координате с нулевым индексом, поскольку эта координата имеет такую же размерность как и остальные координаты [см]. Однако, для получения обычного трехмерного уравнения движения необходимо перейти к дифференцированию по времени . Умножим обе части полученного уравнения на квадрат скорости света и получим уравнение движения в обычном трехмерном виде:

$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2} = -c^2 \Gamm... ...tyle d t} \rbrace {\displaystyle d x^i\over\displaystyle d t} \end{displaymath}$

(8.9)

Сравнивая обычное уравнение движения в ньютоновской гравитации:

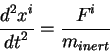
$\begin{displaymath} {\displaystyle d^2 x^i\over\displaystyle d t^2}= {\displaystyle F^i\over\displaystyle m_{inert}} \end{displaymath}$

можно сделать вывод о том, что аналогом ньютоновской силы является член вида:

$\begin{displaymath} F^i_{grav}= - m_{grav} c^2 \Gamma^i_{00} \end{displaymath}$

Из приведенного уравнения видно, что (8.9) содержит члены разных порядков по отношению характерной скорости движения пробной частицы к скорости света. Самый большой член - сила Ньютона, но существуют и более слабые силы, которые, тем не менее вносят вклад в движение частицы в гравитационном поле. Они называются постньютоновскими поправками.

Более полный анализ уравнений движения, в частности вклада постньютоновских поправок мы проделаем позже.

8.3 Девиация геодезический линий

Девиацией двух бесконечно близких геодезических линий называется отклонение этих линий между собой.

Рассмотрим две бесконечно близкие геодезические линии. Одна линия характеризуется несколькими параметрами. Выберем два из них. Один параметр назовем $\lambda$ , он будет афинным параметром вдоль линии. Второй параметр выберем так, чтобы он отсчитывался вдоль направления вектора, который соединяет две указанные геодезические линии и является перпендикулярным вектору, касательному первой геодезической линии. Этот параметр назовем $\eta$ . Теперь уравнение геодезической являетмя функцией двух параметров $x^{\alpha}(\lambda, \eta)$ . Первый параметр $\lambda$ отчитывает длину вдоль геодезической, второй параметр $\eta$ отсчитывает "номер" геодезической линии, координату в перпендикулярном направлении.

Вектор касательный к траектории геодезической линии, как прежде будем обозначать $u^{\alpha}$ . Введем второй вектор $v^{\alpha}$ , который будет касательным к линии, соединяющие две геодезические. Отметим полезное равенство:

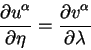
$\begin{displaymath} {\displaystyle\partial u^{\alpha}\over\displaystyle\partial ... ...ystyle\partial v^{\alpha}\over\displaystyle\partial \lambda} \end{displaymath}$

Докажем еще одно равенство, важное для наших рассуждений. Рассмотрим ковариантную производную от вектора $v^{\alpha}$ вдоль геодезической:

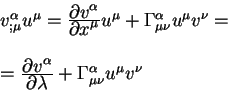
$\begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}= {\displaystyle\... ...ambda} + \Gamma^{\alpha}_{\mu \nu} u^{\mu} v^{\nu} \end{array}\end{displaymath}$

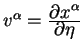Спомним теперь, что вектор $v^{\alpha}={\displaystyle\partial x^{\alpha}\over\displaystyle\partial \eta}$ . Поскольку можно поменять частные производные местами, то производную от вектора $v^{\alpha}$ по параметру $\lambda$ можно записать, как производную от вектора $u^{\alpha}$ по параметру $\eta$ . Поэтому можно продолжить верхнее равенство как:

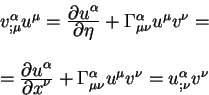
$\begin{displaymath} \begin{array}{l} v^{\alpha}_{; \mu} u^{\mu}={\displaystyle\p... ...u \nu} u^{\mu} v^{\nu} =u^{\alpha}_{;\nu}v^{\nu} \end{array} \end{displaymath}$

Теперь выпишем само равенство, которое было доказано:

$\begin{displaymath} v^{\alpha}_{; \mu} u^{\mu} = u^{\alpha}_{; \mu} v^{\mu} \end{displaymath}$

(8.10)

Рассмотрим теперь как меняется вектор $v^{\alpha}$ вдоль геодезической линии. Поскольку длина этого вектора является расстояние между геодезическими, то сам вектор показывает как меняется расстояние и ориентация двух пробных частиц, которые движутся по геодезическим линиям в гравитационном поле. В обычной ньютоновской теории тяготения, изменение расстояния между пробными частицами вызывается приливными силами. Найдем аналог приливных сил в ньютоновской механики в общей теории относительности.

Для этого рассмотрим вначале первую ковариантную производную от вектора $v^{\alpha}$ вдоль геодезической:

$\begin{displaymath} {\displaystyle Dv^{\alpha}\over\displaystyle d \lambda} = v^{\alpha}_{;\gamma}u^{\gamma} \end{displaymath}$

Поскольку производная по параметру $\lambda$ может быть выражена как производные по координатам, умноженные на вектор вдоль геодезической. Точно так же можно выразит и вторую производную.

Рассмотрим теперь вторую производную от вектора $v^{\alpha}$ вдоль геодезической:

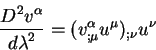
$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = (v^{\alpha}_{;\mu}u^{\mu})_{; \nu} u^{\nu} \end{displaymath}$

В этом равенстве прием перехода от дифференцирования по афинному параметру к дифференцированию по координатам применен дважды. Воспользуемся также равенством (8.10) и выразим величину в круглых скобках через производную от вектора касательного к геодезической, тогда получим:

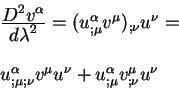
$\begin{displaymath} \begin{array}{l} {\displaystyle D^2 v^{\alpha}\over\displays... ...u^{\nu} + u^{\alpha}_{;\mu}v^{\mu}_{; \nu} u^{\nu} \end{array}\end{displaymath}$

В первом члене меняем порядок ковариантного дифференцирования:

$\begin{displaymath} u^{\alpha}_{;\mu ; \nu} = u^{\alpha}_{;\nu ; \mu} - R^{\alpha}_{\rho \mu \nu} u^{\rho}, \end{displaymath}$

а ко второму вновь применяем равенство (8.10). Получаем, что вторая ковариантная производная от вектора $v^{\alpha}$ есть:

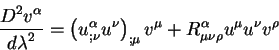
$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2}... ...v^{\mu} + R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath}$

Обратим внимание на то, что в тензоре кривизны изменен порядок индексов, поэтому и знак перед тензором поменялся. Первый член равен нулюб в силу уравнения геодезической линии (см. (6.17)).

Поэтому окончательно вторая ковариантная производная от вектора $v^{\alpha}$ равна:

$\begin{displaymath} {\displaystyle D^2 v^{\alpha}\over\displaystyle d \lambda^2} = R^{\alpha}_{\mu \nu \rho} u^{\mu} u^{\nu} v^{\rho} \end{displaymath}$

(8.11)

Умножая это уравнение на величину $\Delta \eta$ - расстояние между геодезическими получаем уравнение для вектора, который соединяет две пробные частиц, которые свободно движутся по двум близким геодезическим линиям.

Это уравнение называется уравнение девиации близких геодезических линий.

<< 7. Тензор кривизны | Оглавление | 9. Уравнения гравитационного поля >>