Astronet Астронет: М. В. Сажин/ГАИШ Теория относительности для астрономов
http://variable-stars.ru/db/msg/1170927/node5.html
Теория относительности для астрономов
<< 3. Ускоренные системы отсчета | Оглавление | 5. Неэвклидова геометрия >>

Разделы

4. Эксперименты по ОТО

Насколько все теоретические оценки, которые обсуждались в предыдущих главах соответствуют действительности? Подтверждены ли эти формулы экспериментом? Как мы уже писали, специальная теория относительности используется при расчетах больших машин для физического эксперимента. Использование общей теории относительности задержалось. Ее начали применять в технологии только последние двадцать лет. Использование ее началось с определения скорости течения времени в гравитационном поле с различным потенциалом. Расскажем об экспериментах, которые положили начало применению общей теории относительности в прикладных целях.

4.1 Эксперименты по проверке скорости хода времени

Первый эксперимент был сделан в 1971 г.[3]. Четверо часов сделанных на основе цезиевых стандартов частоты были помещены на два самолета и совершили кругосветное путешествие. Одни часы путешествовали в восточном направлении, другие обогнули Землю в западном направлении. Разница в скорости хода времени возникала из-за добавочной скорости вращения Земли. Это был эффект, скорее специальной теории относительности, чем общей, однако, член зависящий от величины земного потенциала в изменении скорости хода часов также присутствовал и внес значимый вклад. Надо сказать, что в первом эксперименте было очень много неопределенностей связанных с неточностью измерения скорости самолетов, высотой самолетов над поверхностью Земли и их положением. Отсутствовал также внешний контроль хода часов и т.п. Тем не менее, удалось подтвердить общую теорию относительности, удалось измерить различие в скорости хода часов на борту двух самолетов. Теоретические вычисления задержки часов были:

Эффект Восток Запад
Потенциальный 144 $\pm$ 14 ns 179 $\pm$ 18 ns
член    
Допплеровский -184 $\pm$ 18 ns 96 $\pm$ 10 ns
член    
Полная -40 $\pm$ 23 ns 275 $\pm$ 21 ns
задержка    

Эксперимент дал следущий результат:

  Восток Запад
Полная -59 ns 273 ns
задержка    

Продемонстрируем на простых выкладках, как меняется собственное время часов, которые находятся на борту двух самолетов, один из которых летит на запад, другой на восток. Скорость самолета относительно земной поверхности обозначим $\vec v_a$. Самолет двигается с поверхности вращающейся Земли, его скорость относительно покоющейся системы координат складывается со скоростью вращения Земли $\vec v_E=\vec \Omega \times \vec r$. Выбирая соответсвующие знаки можно это равенство записать также $v_E=\Omega r \cos \varphi$. Здесь $\varphi$ - геоцентрическая широта, которая может быть отождествлена с обычной географической широтой, поскольку сжатие Земли мало $\sim 0.003$ и при наших вычислениях им можно пренебречь.

В системе координат, которая связана со центром Земли, который находится в состоянии свободного падения в поле тяжести Солнца и планет, время отсчитывается собственными часами $t$. В этой же системе координат скорость самолета есть:

\begin{displaymath} \vec V_a = \vec v_a + \vec \Omega \times r_a \end{displaymath}

Разность собственного времени двух часов $\tau_1$ и $\tau_2$ определяется равенством:

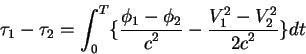
\begin{displaymath} \tau_1 - \tau_2 = \int_0^T \lbrace{\displaystyle\phi_1 - \ph... ...\displaystyle V_1^2 - V_2^2\over\displaystyle 2c^2}\rbrace d t \end{displaymath}

Подставляя формулу для скорости самолета относительно центра системы координат получаем, что на борту самолета который летит на восток, скорость течения времени отличается от скорости течения времени на борту самолета, который летит на запад. Эта разность составляет

\begin{displaymath} 2 v_{ae} \Omega r_a \cos \varphi \end{displaymath}

Здесь $v_{ae}$ - компонента скорости самолета, направленная на восток. При этом считается, что скорости самолета, который летит на запада и самолета, летящего на восток равны друг другу.

Отсюда видно, что предсказания общей теории относительности были подтверждены с высокой (для того времени) точностью.

Измерения временной задержки зависящей от потенциала были сделаны четыре года спустя [4]. Исследователи синхронизовали двое часов, затем поместили одни часы на вершину горы, а вторые оставили на физическом факультете, расположенном у подножья горы. Разница в высоте составляла 3250 м. Время за которое измерялась задержка часов составляло 66 дней. Из - за различия в потенциале гравитационного поля Земли скорости хода часов были различны. Измерения опять подтвердили общую теорию относительности и измерили задержку с точностью $15\%$.

Два года спустя подобный эксперимент был повторен в Японии [5]. Исследователи поместили одни часы на гору, а другие под гору. Разница высот составляла 2818 м, а время измерения эффекта было две недели. Поскольку часы, используемые японскими исследователями были значительно точнее, точность измерений составляла 5%. Вновь предсказания общей теории относительности были подтверждены.

Одни из наиболее точных измерений были сделаны во время высотного полета ракеты [6]. На борту ракеты находился водородный мазер, который использовался в качестве высокостабильных часов. Ракета поднялась на 10 000 м, а затем упала в Атлантический океан. Для измерений потенциального члена в задержке часов пришлось компенсировать вклад допплеровского члена (ракета двигалась быстро), а также ионосферные эффекты. Тем не менее измерения были благополучно проведены и правильность формулы для времени задержки была подтверждена с точностью 0.01%.

Измерения времени задержки проводились также позже на самолетах. В полете осуществлялся постоянный контроль хода часов и стабильности параметров. В частности, был проведен эксперимент по проверке "парадокса близнецов". Были синхронизованы часы, после чего одни часы поместили на борт самолет, а вторые оставили на Земле. Часы, которые находились на борту самолета, по прилету показали, что на борту прошло больше времени, чем на Земле!

В чем дело? Может быть общая теория относительности неверна? Нет, измерения вновь полностью подтвердили справедливость общей теории относительности, просто надо делать правильные выводы из теоретических положений.

Классическая формулировка парадокса близнецов относиться к системам координат, которые свободны от неоднородного гравитационного поля. На Земле, разумеется, неоднородное гравитационное поле присутствует. Поэтому надо не только сравнивать задержку времени возникающую на борту самолет из - за движения самолет, но также и задержку времени возникающую из - за потенциального члена. Если самолет движется относительно лаборатории (пробных часов), то часы на его борту будут отставать от часов в лаборатории (это эффект пропорциональный $-{\displaystyle v^2\over\displaystyle 2c^2}$), но самолет летит выше лаборатории, он летит в поле тяжести с ослабленным потенциалом, а значит, часы, находящиеся в лаборатории будут идти медленнее по сравнению с часами, находящимися на борту $+{\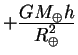displaystyle GM_{\oplus} h\over\displaystyle R^2_{\oplus}}$ (Здесь $h$ -разница высот между самолетом и лабораторией). Сравнить вклад потенциального члена и члена из - за скорости легко. Необходимо сравить величину характерной скорости в данном потенциале (вторая космическая скорость) с реальной скоростью аппарата.

Для самолет потенциальный член всегда больше. Скорость самолет значительно меньше скорости ракеты, поэтому часы, поднятые на самолете над лабораторией (если они, конечно, подняты на достаточно большую высоту) будут отставать по сравнению с часами, находящимися в лаборатории.

Теперь формулы для изменения темпа течения времени в зависимости от скорости и высоты используются в навигационной технологии GPS и ГЛОНАСС.

4.1.1 Парадокс близнецов

Рассмотрим теперь "парадокс близнецов" в его классической формулировке. Итак, рассматриваются двое часов, одни для простоты будем обозначать $A$, вторые $B$. Часы $A$ все время покоются относительно инерциальной системы координат $K$. Часы $B$ вначале тоже покоются. Часы синхронизируются, затем часы $B$ начинают ускоряться вдоль положительных значений оси $Ox$ системы координат $K$. Через некоторое время ускорение пропадает и часы $B$ по инерции движутся со скоростью $v$ вдоль оси $Ox$ некоторое время. Затем часы вновь ускоряются, но теперь в противоположном направлении, что приводит к их замедлению и полной остановке, а затем к началу движения в противоположном направлении. Часы $B$ ускоряются пока не достигнут скорости $-v$. Затем часы $B$ движутся в направлении к часам $A$. В заранее расчитанный момент времени часы $B$ вновь начинают ускоряться в направлении противоположном движению так, чтобы скорость их уменьшалась. Ускорение вновь подбирается так, чтобы часы $B$ оказались в одной точке с часами $A$ c нулевой скоростью. После этого показания часов сравниваются. Ускорения в этом мысленном эксперименте можно сделать достаточно большими, так что влияние участков движения с ненулевым ускорением на процесс вычисления задержки часов можно считать пренебрежимо малым. Тогда часы $B$ должны отстать от часов $A$ на некоторый интервал времени. Итак, для наблюдателя, сопутствующего часам $A$ движущиеся часы должны отстать.

Рассмотрим этот же процесс с точки зрения наблюдателя сопутствующего часам $B$. Он имеет противоположные характеристики, так что с его точки зрения "отстать" должны часы $A$. Ниже мы проанализируем правильный ход рассуждений и покажем, что на самом деле для обеих наблюдателей часы $B$ должны отстать по сравнению с часами $A$. Причиной неправильных рассуждений является наличие поля ускорения в системе координат сопутствующей часам $B$. Поэтому изменения интервалов времени в системе сопутствующей $B$ надо считать уже по формулам общей теории относительности, а не только по формулам специальной теории относительности.

Одно из лучших изложений "парадакса близнецов" привел А.Эйнштейн в своей популярной статье "Диалог по поводу возражений против теории относительности" приведенной в книге [7]. Будем следовать этому изложению, подкрепляя его расчетами. Весь процесс путешествия и возвращения часов можно разделить на пять стадий.

С точки зрения $A$      С точки зрения $B$
1. Часы $B$ ускоряются внешними силами в направлении положительных значений оси $Ox$, пока не приобретут скорость $v$. Часы $A$ покоются.     1. В отрицательном направлении оси $Ox$ возникает гравитационное поле, в котором $A$ падает ускоренно. Часы $B$ удерживаются внешними силами в покое. Когда $A$ приобретают скорость $v$ гравитационное поле исчезает.
2. Часы $B$ движутся с постоянной скоростью до точки 2. Часы $A$ покоятся.     2. Часы $A$ движутся с постоянной скоростью до точки $\hat 2$. Часы $B$ покоятся.
3. Часы $B$ ускоряются внешними силами пока не приобретут скорость $-v$.     3. Появляется однородное поле тяжести направленое в сторону положительных значений оси $Ox$, под действием которого $A$ ускоряются в положительном направлении до тех пор пока не приобретут скорость $+v$. После этого поле исчезает. Внешние силы удерживают часы $B$.
4. Часы $B$ движутся назад с постоянной скоростью $v$, пока не приблизятся к $A$. Часы $A$ покоятся.     4. Часы $A$ движутся со скоростью $v$ в направлении положительных значений оси $Ox$, до тех пор, пока не приблизятся к $B$. Часы $B$ остаются в покое.
5. Часы $B$ останавливаются внешними силами.     5. Возникает поле тяжести, которое останавливает часы $A$. Часы $B$ удерживаются внешними силами.

Как видим, две системы координат неэквивалентны друг другу. С точки зрения наблюдателя сопутсвующего часам $A$ гравитационное поле отсутствует, с точки зрения наблюдателя сопутствующего часам $B$ гравитационное поле не равно нулю. Для вычисления скорости хода часов с точки зрения наблюдателя $A$ достаточно формул, выведенных в рамках СТО, с точки зрения наблюдателя $B$ при вычислении скорости хода времени необходимо учитывать эффекты ОТО.

Вновь аккуратно учитывая разницу между системами координат вычислим скорость хода часов в системе $K$ и в системе $\hat K$ и сравним какие из часов отстануть от других.

Расчет будем вести применяя приближенные формулы СТО и ОТО для того, чтобы расчеты были легче и не затемнялся смысл формул, мы будем считать, что скорость $v$ значительно меньше чем скорость света.

Вначале рассчитаем задержку времени по формулам СТО с точки зрения наблюдателя сопутствующего часам $A$. Будем считать, что время ускорения пренебрежимо мало. Тогда разность скорости хода часов во время первой стадии, а также во время третьей и пятой стадии ппренебрежимо мало. Тогда интервал времени показанный часами в течении всего путешествия $B$ зависит от интервала времени показанному часами $A$ как:

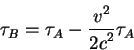
\begin{displaymath} \tau_B=\tau_A - {\displaystyle v^2\over\displaystyle 2c^2}\tau_A \end{displaymath}

Здесь $\tau_A$ - полное время путешествия туда - обратно.

Итак с точки зрения наблюдателя сопутствующего часам $A$ часы $B$ отстают.

Проведем расчет скорости хода обеих часов с точки зрения наблюдателя сопутствующего часам $B$. Во время первой стадии разность хода пренебрежимо мала. Оба чдена дают пренебрежимо малый вклад. Потенциальный - потому что часы $A$ и $B$ находятся практически только в одной точке, а вклад от потенциального члена пропорционален разности расстояний, член зависящий от скорости тоже мал.

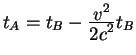Во время второй стадии движения по инерции, которая длится время, скажем, $t_B$ часы $A$ отстают от часов $B$ как $t_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B$.

Будем считать, что третья стадия длится интервал времени $t_r$. Во время третьей стадии вклад члена пропорционального скорости часов в разность хода часов пренебрежимо мал. Однако велик вклад потенциального члена. Действительно за время $t_B$ часы $A$ прошли относительно часов $B$ расстояние $L=vt_B$. Ускорение, требуемое для изменения скорости с $+v$ на $-v$ в течении времени $t_r$ составляет $g={\displaystyle 2v\over\displaystyle t_r}$.

Гравитационный потенциал между точками нахождения двух часов составляет величину $\phi= +gL$. Знак плюс выбран потому, что ускорение направлено от $A$ к $B$. После окончания третьей стадии из - за потенциального члена интервал времени $T_A$ показанный часами $A$ и интервал времени $T_B$ показанный часами $B$ связаны равенством

\begin{displaymath} T_A=T_B +\frac{gL}{c^2} t_r \end{displaymath}

Обратим внимание, что второе слагаемое в этой формуле имеет положительный знак. Это означает, что часы $A$ теперь идут быстрее, чем часы $B$.

В течении четвертой стадии часы $A$ вновь отстают от часов $B$. Обратный путь длится тот же интервал времени $\hat t_B=t_B$. За этот интервал часы $A$ вновь отстают. Интервал времени, который показывают часы $A$ составляет:

\begin{displaymath} \hat t_A=\hat t_B -\frac{v^2}{2c^2}\hat t_B \end{displaymath}

В течении пятой стадии часы $A$ вновь замедляются гравитационным полем. Однако теперь разность хода часов $A$ и $B$ опять пренебрежимо мала, по тем же причинам, что и на первой стадии.

Посчитаем полный интервал времени, который показывают часы $A$ с точки зрения наблюдателя, сопутствующего часам $B$. Промежуток времени, который показывают часы $A$ складывается из промежутков времени показываемых этими часами с первой по пятую стадии:

\begin{displaymath} \hat \tau_A=t_A +T_A +\hat t_A \end{displaymath}

Поэтому полный интервал времени показанный часами $A$ с точки зрения наблюдателя сопутствующего часам $B$ есть:

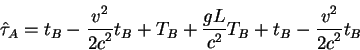
\begin{displaymath} \hat \tau_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t... ...c^2} T_B + t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B \end{displaymath}

Подставим значение полного врмени путеществия туда - обратно $\tau_B=2t_B$. Кроме того, подставим значения $g={\displaystyle 2v\over\displaystyle T_B}$ и $L=vt_B$, выражая полное равенство только через $v$. Окончательно получаем, что

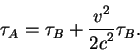
\begin{displaymath}\tau_A=\tau_B +{\displaystyle v^2\over\displaystyle 2c^2}\tau_B.\end{displaymath}

Теперь видно, что интервал времени показываемый часами $A$ оказывается больше, чем интервал времени показываемый часами $B$. Это значит, что путешествующие часы покажут меньший промежуток времени, чем часы покоящиеся относительно инерциальной системы координат. Этот расчет демонстрирует отсутствие "парадокса близнецов" в релятивистской физике.


<< 3. Ускоренные системы отсчета | Оглавление | 5. Неэвклидова геометрия >>

Rambler's Top100 Яндекс цитирования