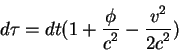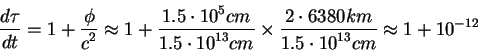Astronet Астронет: М. В. Сажин/ГАИШ Теория относительности для астрономов
http://variable-stars.ru/db/msg/1170927/node4.html
Теория относительности для астрономов
<< 2. Специальная теория относительности | Оглавление | 4. Эксперименты по ОТО >>

Разделы

3. Ускоренные системы отсчета и СТО

Успех специальной теории относительности, правильное формулирование принципа относительности для инерциальных систем отсчета движущихся со скоростями близкими к скорости света побудил А.Эйнштейна на распространение этого принципа на ускоренные системы отсчета.

Теперь вкратце расскажем как А.Эйнштейн смог описать ускоренные системы отсчета в терминах принципа относительности, как стало понятно, что это описание приводит к геометрической трактовке гравитационного поля, необходимости введения неэвклидовой геометрии в физику и идеи искривленного пространства - времени. Основная идея стала понятной А.Эйнштейну в 1907 г., хотя в оригинальном виде она была опубликована только в 1972 г. в газете "New York Times". Это идея позже получила название релятивистского принципа эквивалентности Эйнштейна. Сам А.Эйнштейн описал то время и мысли в отрывке, который помещен ниже. Перевод этого на русский язык слишком красив, чтобы его опустить:

" Я пытался модифицировать теорию гравитации Ньютона таким образом, чтобы она точно соответствовала специальной теории относительности. Попытки сделать это показали, что теория гравитации может быть согласована с принципами специальной теории относительности, но они не удовлетворяли меня, поскольку требовали введения гипотез не содержащих физических основ. В это время ко мне пришла счастливейшая идея моей жизни 3.1 в следущем виде:
Точно также, как электрическое поле создается электромагнитной индукцией, гравитационое поле может существовать только относительно. Следовательно, для наблюдателя, находящегося в свободном падении с крыши дома, гравитационного поля не существует ( по крайней мере в бесконечно близкой его окрестности ) в течении всего времени падения. Если наблюдатель выпустит из рук какие - либо предметы они остануться относительно этого наблюдателя в состоянии покоя независимо от их химического состава или физического состояния 3.2. Наблюдатель в этом случае должен признать, что он находится в состоянии покоя.

Чрезвычайно интересный эмпирический закон гласящий, что все тела в одном и том же гравитационном поле падают с одним и тем же ускорением, получал в этом случае глубокий физический смысл. Если бы нашелся хотя бы один предмет, который падал бы в гравитационном поле не так как другие, то наблюдатель сравнивая свое движение с движением этого предмета смог бы сказать, что он находится в гравитационном поле и что он падает под его воздействием. Но если такого предмета не существует, а эксперимент подтверждает этот факт с большой степенью точности, наблюдатель теряет всякое объективное основание рассматриваться свое состояние как состояние падения в гравитационном поле. Скорее он имеет право рассматривать свое состояние как состояние покоя и считать, что в его ближайшем окружении гравитационное поле отсутствует.

Таким образом, известный экспериментальный факт, что ускорение в гравитационном поле не зависит от химического состава или физического состояния становится могучим аргументом для распространения принципа относительности на координатные системы, которые движутся неравномерно одна относительно другой."

3.1 Включение гравитации в СТО.

Рисунок 3.1: На рисунке изображен лифт, в котором ускорение моделирует поле тяжести.
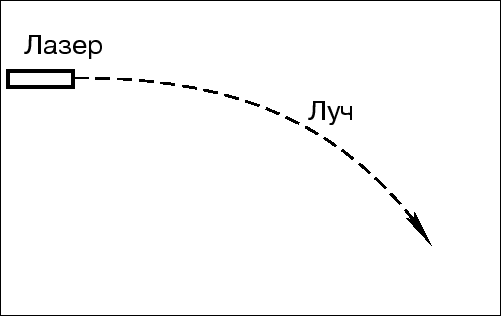
\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig3_1.ai}}\end{figure}

Рассмотрим на рис. 3.1 пояснения к принципу эквивалентности Эйнштейна, который распространяет принцип относительности на ускоренные системы координат.

На левом рисунке изображен лифт, ускоряемый вверх с величиной ускорения равной $a$. Свет, изображенный на рисунке пунктриной линией движется в таком лифте по искривленной траектории. Эта искривленная траектория является идеально прямой линией, но в покоящейся системе отсчета. В ускоренной системе отсчета линия становится искривленной. На правом рисунке изображен тот же самый лифт, который находится в поле тяжести с однородным ускорением. Принцип относительности примененный к ускоренным системам отсчета гласит, что невозможно отличить две этих ситуации. Значит, в лифте, который находится в гравитационном поле свет тоже должен двигатся по искривленной траектории.

Вычислим характеристики света при движении в однородном поле тяжести пользуясь характеристиками света в ускоренном лифте. Для этого рассмотрим фотоны, которые распространяются вдоль поля тяжести $\vec g$. Это гравитационное поле исходя из принципа эквивалентности можно заменить полем ускорения с равной величиной, но противоположным знаком. Рассмотрим лазер $L$, который излучает фотоны с частотой $\nu_0$ (эта частота измеряется наблюдателем, находящимся рядом с лазером, т.е. сопутствующего лазеру). На расстоянии $l$ от лазера (по направленнию движения) находится другой наблюдатель $O$, который тоже измеряет параметры света. 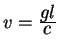Свет, который вышел из лазера в момент времени $t=0$ достигнет наблюдателя $O$ в момент времени $t={\displaystyle l\over\displaystyle c}$, а сам наблюдатель будет иметь скорость относительно лазера равную $v={\displaystyle gl\over\displaystyle c}$.

Рассмотрим теперь две дополнительные инерциальные системы координат, которые двигаются равномерно и прямолинейно, так что ускорение в этих системах равно нулю. В первой системе координат $K_1$ в начале системы находится наблюдатель $O_1$. Скорость и положение этой системы выбраны так, чтобы в момент врмени $t=0$ наблюдатель $O_1$ находился в бесконечно малой окрестности точки $L$ ускоренной системы координат. Вторая инерциальная система движется со скоростью $v$ относительно первой так, чтобы в момент времени $t={\displaystyle l\over\displaystyle c}$ ее начало, в котором нахордится наблюдатель $O_2$ совпало с положением наблюдателя $O$, находящегося в ускоренной системе координат.

Привлечение дополнительных инерциальных систем координат сделано не для того, чтобы запутать студента, а для того, чтобы провести расчеты характеристик света пользуясь уже знакомыми формулами специальной теории относительности.

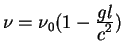
Частота фотона измеренная наблюдателем $O_1$ в момент времени $t=0$ есть $\nu_0$, согласно нашему определению. В момент времени $t$ частота того же фотона, измеренная наблюдателем $O_2$, движущемся со скоростью $v$ относительно $O_1$ есть $\nu=\nu_0(1-{\displaystyle gl\over\displaystyle c^2})$

Лазер представляет из себя стандартный электромагнитный осциллятор с собственнолй частотой $\nu_0$ и с периодом $P_0={\displaystyle 1\over\displaystyle\nu_0}$. Соответственно, наблюдатель $O$ будет измерять период осциллятора:

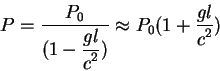
\begin{displaymath} P={\displaystyle P_0\over\displaystyle(1-{\displaystyle gl\o... ...^2})} \approx P_0(1+ {\displaystyle gl\over\displaystyle c^2}) \end{displaymath}

Произведение ускорения на расстояние представляет разность гравитационных потенциалов между двумя точками. В первой точке находится лазер, во второй нахаодится наблюдатель: $\phi=gl$. Теперь можно привести формулу определяющую темп течения времени в двух точках $L$ и $O$:

\begin{displaymath} \tau=t(1 +{\displaystyle\phi\over\displaystyle c^2}) \end{displaymath} (3.1)

Подставим эту формулу в уравнение для четырехмерного интервала. Поскольку (3.1) представляет связь собственного времени точки $O$, т.е. $\tau$ с координатным временем $t$ (которое мы относим к собственному времени точки $L$, в которой потенциал нулевой), то можно записать четырехмерный интервал как функцию собственного времени и как функцию координатного времени:

\begin{displaymath} ds^2=c^2 d\tau^2=(1 +{\displaystyle 2\phi\over\displaystyle c^2})\times c^2\; dt^2 \end{displaymath} (3.2)

Основное изменение по сравнению с прежней величиной, которая характеризовала "расстояние" между событиями в СТО - появление коэффицента перед квадратом дифференциала времени. Этот коэффицент, вообще говоря, является функцией всех четырех координат. Такие функции появляются в том случае, когда метрика является неэвклидовой, а геометрия описывает искривленное пространство - время. Поэтому новая физика - описание сильных гравитационных полей - характеризуется неэвклидовой геометрией. Для работы в общей теории относительности необходимо владеть аппаратом неэвклидовой геометрии, которая будет излагаться позже в этом курсе.

Вернемся к формуле (3.2). В том случае, когда наблюдатель движется в поле $\phi$ со скоростью $v$, то его собственное время $\tau$ связано с координатным временем $t$ как:

\begin{displaymath} d\tau=dt(1 +{\displaystyle\phi\over\displaystyle c^2} -{\displaystyle v^2\over\displaystyle 2c^2}) \end{displaymath} (3.3)

Для того, чтобы оценить скорость течения времени в гравитационном потенциале различной величины проведем расчет на сколько "уходят" друг относительно друга часы, находящиеся на полуденной и полуночной стороне Земли в гравитационном поле Солнца. Будем считать, что член пропорциональный квадрату скорости наблюдателей различается для двух наблюдателей на пренебрежимо малую величину. Оценивать разность скорости течения времени будем только по формуле (3.3).

\begin{displaymath} {\displaystyle d\tau\over\displaystyle dt}=1 +{\displaystyle... ...m\over\displaystyle 1.5 \cdot 10^{13} cm}\approx 1 +10^{-12} \end{displaymath} (3.4)

Это значит, что, скажем, за 12 часов двое часов "разойдутся" на время равное $\sim$ 220 наносекунд. Это вполне обнаружимое, а для некоторых процессов даже большое время. Б$\grave o$льшее время покажут часы, которые расположены дальше от Солнца - часы на полуночной стороне Земли. На рис. 3.1 показан график скорости хода часов в зависимости от расстояния от барицентра Солнца. Вот только для обнаружения этой разницы в скорости течения времени необходимо находиться далеко от Земли, например, на Солнце.

Тем не менее измерить подобный эффект можно также и на Земле и в ближнем космосе. Рассмотрим два интересных эффекта - изменение скорости хода часов в зависимости от сезона и изменение скорости хода часов установленных на спутнике системы GPS по сравнению с часами установленными на Земле.

Ось вращения Земли наклонена по отношению к плоскости земной орбиты на угол $\sim 23^{\circ}.5$. Поэтому часы, скажем 1 и 2 с собственным временем $\tau_1$ и $\tau_2$, которые находятся на разных широтах, соответственно $\varphi_1$ и $\varphi_2$, находятся также при разных значениях гравитационного потенциала Солнца. Естественно, что при движении Земли по орбите возникает годовая гармоника в изменении скорости хода часов:

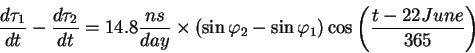
\begin{displaymath} {\displaystyle d \tau_1\over\displaystyle d t} - {\displayst... ...t( {\displaystyle t - 22 June\over\displaystyle 365} \right) \end{displaymath}

Здесь в качестве начала отсчета выбран день летнего солнцестояния. На коротких промежутках времени, значительно меньших длительности года такое изменение скорости течения времени воспринимается как линейный дрейф часов, зависящий от широты! Величина этого дрейфа $\sim$ 15 наносекунд в день. Такой эффект действительно наблюдается и природа его никак необъяснима, если "забыть" про эффекты общей теории относительности.

Общая теория относительности изменила наши взгляды на структуру пространства и времени. В течении долгого времени ОТО оставалась теоретическим инструментом современной физики, который не имеет приложений в технологии. Ситуация существенно измениласьс появлением высокоточной навигации, с появлением спутниковых систем GPS и ГЛОНАСС. Теперь для целей точной навигации (на поверхности Земли) необходимо использовать уравнения общей теории относительности для редукции наблюдений. Особенно важно использовать их для пересчета стандартов времени на Земле и на спутниках. Высота полета спутников превышает земной радиус, а скорость значительно превышает скорость полета современных самолетов. Поэтому изменение скорости течения времени особенно заметны. Собственноре время на борту спутника обозначим $\tau_s$, а на поверхности Земли обозначим $\tau_e$. Отношение двух интервалов составляет:

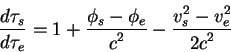
\begin{displaymath} {\displaystyle d \tau_s\over\displaystyle d \tau_e} = 1 + {\... ...c^2} - {\displaystyle v_s^2 - v_e^2\over\displaystyle 2 c^2} \end{displaymath}

Здесь индексы $s$ и $e$ соответственно относятся к потенциалу Земли на высоте полета спутника и скорости его полета, а также соответствующие величины для стандарта на Земле.

Итак, скорость течения времени на Земле и на спутнике различна. Для спутников системы GPS, которые находятся на высоте 14 000 км отличие двух темпов течения времени составляет 44 микросекунды в день. Естественно, для поддержания равномерной шкалы времени, единой для поверхности Земли и спутников необходимо учитывать это изменение.


<< 2. Специальная теория относительности | Оглавление | 4. Эксперименты по ОТО >>

Rambler's Top100 Яндекс цитирования