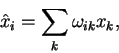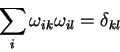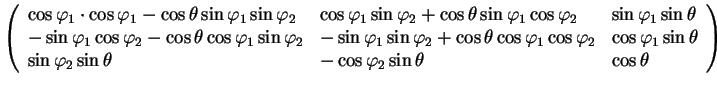|
Астронет: М. В. Сажин/ГАИШ Теория относительности для астрономов http://www.astronet.ru/db/msg/1170927/node2.html |
<< Введение | Оглавление | 2. Специальная теория относительности >>
- 1.1 Принцип относительности Галилея
- 1.2 Трудности классической механики при описании распространения света
- 1.3 Специальная теория относительности
1. Принципы относительности
1.1 Принцип относительности Галилея
Первый принцип относительности (ПО) был сформулирован еще в эпоху Возрождения Г.Галилеем. ПО относился к механике и гласил: "Законы механики в системе координат, движущейся равномерно и прямолинейно в пространстве, имеют тот же вид, что и в системе координат, покоящейся в пространстве".
Из этого постулата можно сделать простой вывод, а именно: существует бесконечно много эквивалентных систем координат, называемых инерциальными и совершающими равномерное и прямолинейное движение или покоящихся друг относительно друга. В этих системах законы механики выполняются в простой классической форме.
Определим сразу, что законами механики здесь будем называть законы движения в классической механике и законы сохранения.
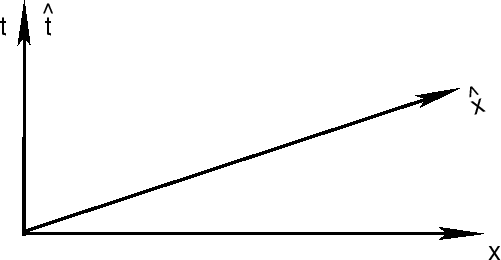
Принцип относительности Галилея на математическим языке преобразования
координат обычно формулируется следущим образом. Пусть положение пробной
частицы описывается в декартовой системе координат
![]() , кроме трех пространственных координат мы добавили временную
координату, которая необходима в специальной теории относительности
(СТО) и общей теории относительности (ОТО),
, кроме трех пространственных координат мы добавили временную
координату, которая необходима в специальной теории относительности
(СТО) и общей теории относительности (ОТО), ![]() . В системе координат
. В системе координат
![]() =
= ![]() ,
, ![]() ,
, ![]() ,
, ![]() , законы механики
остаются неизменными, если система
, законы механики
остаются неизменными, если система ![]() движется относительно
системы координат
движется относительно
системы координат ![]() со скоростью
со скоростью ![]() , так, что две системы координат
связаны между собой преобразованием Галилея:
, так, что две системы координат
связаны между собой преобразованием Галилея:
 |
В частности из принципа относительности Галилея вытекал закон сложения
скоростей:
| (1.2) |
Законы механики остаются неизменными также в системах координат, оси которых повернуты друг относительно друга. Поскольку астрономы - наблюдатели с преобразованиями типа поворота имеют дело повседневно, обсудим их более подробно.
1.1.1 Вращения в трехмерном пространстве
На языке математики преобразования Галилея называются преобразованиями трехмерной системы координат. Преобразования типа (1.1) называются преобразованием сдвига. Помимо сдвига в трехмерном пространстве также часто используют преобразование вращения.
Рассмотрим все вращения трехмерного пространства вокруг одной фиксированной
точки - начала координат. В ортогональной системе координат трехмерного
пространства вращение задается уравнением
Кроме того, при вращении остается инвариантной форма вида:
Поэтому можно получить уравнение для коэффицентов
матрицы вида:
Матрицы удовлетворяющие уравнению (1.4) называются ортогональными матрицами. Если вычислить детерминант обеих частей
уравнения (1.4), то получим условие вида
![]() , что дает два возможных знака детерминанта:
, что дает два возможных знака детерминанта:
Знак
Рассмотрим вращения.
Прежде всего проанализируем две системы координат на плоскости. Одну
систему координат будем обозначать ![]() , вторую -
, вторую - ![]() . Будем считать,
что центры этих систем совпадают, а оси повернуты друг относительно друга
на угол
. Будем считать,
что центры этих систем совпадают, а оси повернуты друг относительно друга
на угол ![]() против часовой стрелки. Тогда преобразования от координат
без крышечки к координатам с крышечкой записываются в виде системы линейных
уравнений:
против часовой стрелки. Тогда преобразования от координат
без крышечки к координатам с крышечкой записываются в виде системы линейных
уравнений:
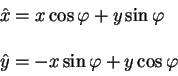
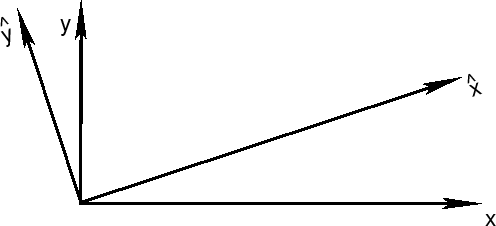 |
Представим это преобразование в матричном виде. Как видно из предыдущей
системы уравнений, вращения совершаются вокруг некоторой оси. Для начала
выберем в качестве оси вращения ось ![]() и совершим вращение на угол
и совершим вращение на угол
![]() . Матрица этого вращения имеет вид:
. Матрица этого вращения имеет вид:
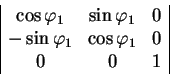
Детерминант такой матрицы равен единице.
Математики характеризуют вращение как некоторый вектор, направленный вдоль оси вращения и равный по величине углу поворота. Для астрономов более привычным является представление вращения в виде трех последовательных положительных вращений на углы Эйлера1.1. Рассмотрим их подробнее.
Полное вращение может быть представлено трех вращений. Первое - вращение
![]() 1.2на угол
1.2на угол ![]() вокруг оси
вокруг оси ![]() , в результате которого ось
, в результате которого ось
![]() займет новое положение
займет новое положение ![]() . Затем вращение
. Затем вращение ![]() вокруг новой
оси
вокруг новой
оси ![]() на угол
на угол ![]() в результате которого ось
в результате которого ось ![]() займет
новое положение
займет
новое положение ![]() , и, наконец, вращение
, и, наконец, вращение ![]() вокруг новой
оси
вокруг новой
оси ![]() в результате которого ось
в результате которого ось ![]() вновь переместится на
угол
вновь переместится на
угол ![]() :
:
| (1.5) |
Элементы полной матрицы вращения
![]() можно найти как произведение трех матриц поворотов вокруг осей
можно найти как произведение трех матриц поворотов вокруг осей ![]() ,
, ![]() ,
,
![]() :
:
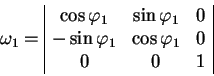 |
(1.6) |
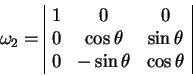 |
(1.7) |
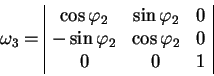 |
(1.8) |
При перемножении матриц необходимо помнить, что они перемножаются в обратном порядке. Перемножив матрицы, получим:
При вращениях углы
Вращение (1.9) имеет обратный элемент. Обратный элемент - это
вращение на такие углы, которые приводят систему координат в прежнее
положение. Он задается другим
вращением, которое совершается на углы Эйлера
![]() ,
, ![]() ,
,
![]() .
.
Остается только добавить, что вращения образуют группу. Элементами группы являются повороты на углы Эйлера. Группа топологически эквивалентна шару, у которого отождествлены диаметрально противоположные точки.
1.1.2 Преобразования на момент наблюдения
В качестве примера приведем матрицу преобразования от координат небесных тел, заданных в каталогах к текущим координатам на данный момент наблюдений.
В каталогах обычно приводятся несколько характеристик некоторой звезды, две
из которых - координаты звезды (ее положение) на небесной сфере ![]() (прямое восхождение) и
(прямое восхождение) и ![]() (склонение) приведенные на определенную
эпоху. Другими словами, указывается положение звезды на определенный
момент времени, скажем, на 1 января 2000 года. Кроме указания эпохи,
необходимо определить саму систему координат и указать начало отсчета
координат1.3.
(склонение) приведенные на определенную
эпоху. Другими словами, указывается положение звезды на определенный
момент времени, скажем, на 1 января 2000 года. Кроме указания эпохи,
необходимо определить саму систему координат и указать начало отсчета
координат1.3.
Полюс мира - точка, на которую опирается полярная ось, вокруг которой вращается Земля - естественная ось для системы координат. Звезды в течении ночи меняют свое положение на небе (факт известный каждому, кто хоть раз наблюдал за ночным небом), лишь обна точка остается неподвижной - полюс мира. Наиболее близко к полюсу (но не точно в полюсе) находится Полярная звезда. Формально полярная ось определяется как ось, проведенная через центр системы координат, параллельная оси вращения Земли [1]. Перпендикулярно полярной оси лежит плоскость экватора.
В астрономии исторически выбирана сферическая система координат связанная с вращением Земли. Полярная ось и экватор служат основными элементами этой системы координат. Угол, который отсчитывается в плсокости экватора называется прямым восхождением, а угол, который отсчитывается вдоль меридиана от плоскости экватора называется склонением. Повторим, что такая система небесных координат возникла исторически в древнем мире и сохраняется в астрономии до сих пор.
Плоскость экватора (или положение полярной оси) определяет начало отсчета
угла по склонению. Вторая основная точка системы координат, начало отсчета
выбирается для того, чтобы указать точку от которой отсчитывается вращение
Земли. Такая точка исторически была выбрана как точка пересечения
небесного экватора и эклиптики. Экватор - плоскость перпендикулярная
полярной оси и прекрасно подходит для задания угловой координаты. Кроме
суточного вращения Земля испытывает еще и годовое вращение вокруг Солнца. В
таком годовом вращении существует полюс эклиптики (ось орбиты Земли вокруг
Солнца) и плоскость эклиптики, которая перпендикулярна полярной оси
эклиптики. Экватор и эклиптика наклонены друг относительно друга на угол
примерно ![]() , точка пересечения используется для определения
начала отсчета прямого восхождения. Остается добавить, что в математической
физике, в сферической системе координат, прямое восхождение
, точка пересечения используется для определения
начала отсчета прямого восхождения. Остается добавить, что в математической
физике, в сферической системе координат, прямое восхождение ![]() обозначается обычно
обозначается обычно ![]() , эквивалентом второй астрономической
координаты - склонения
, эквивалентом второй астрономической
координаты - склонения ![]() является сферическая координата
является сферическая координата
![]() .
.
Такое определение астрономической системы координат сохранялось в течение
многих веков. В последнее десятилетие произошло существенное изменение. В
1991 г. Международный Астрономический Союз (МАС или IAU - английская
абревиатура) принял новую астрономическую систему координат основанную на
наблюдениях радиоисточников. Эту систему назвали ICRF 1.4. Это высокоточная система координат,
достаточно сказать, что современная точность положений так называемых
определяющих источников - десятки микросекунд дуги. По определению системы
ICRF в качестве экватора выбирается плоскость, которая совпадает со средним
экватором на эпоху J2000.0, а также в качестве полярной оси выбирается ось
совпадающая с полярной осью каталога FK5. Таким образом, начало отсчета
склонения определяется также от экватора новой системы. Несколько по
другому определяется точка отсчета прямого восхождения. В соответствии с
рекомендациями IAU начало отсчета по ![]() теперь выбирается следущим
образом. Оно выбирается как можно ближе к динамической точке весеннего
равноденствия на эпоху J2000.0, хотя и другим способом. А именно, началом
отсчета выбрано среднее положение 23 радиоисточников, входящих в список
источников, определяющих ICRF. Причем в радиокаталогах, эти источники
смещены так, чтобы прямое восхождение квазара 3C273 B совпадало с
оптической координатой
теперь выбирается следущим
образом. Оно выбирается как можно ближе к динамической точке весеннего
равноденствия на эпоху J2000.0, хотя и другим способом. А именно, началом
отсчета выбрано среднее положение 23 радиоисточников, входящих в список
источников, определяющих ICRF. Причем в радиокаталогах, эти источники
смещены так, чтобы прямое восхождение квазара 3C273 B совпадало с
оптической координатой ![]() этого квазара.
этого квазара.
Звезды обладают собственным движением, поэтому их положения меняются, изменение положения характеризуется собственными движениями (угловыми скоростями звезд по небу). Помимо этого, индивидуального для каждой звезды движения, существует единое движение всей небесной cистемы. Это движение связано с изменением ориентации Земли в космическом пространстве. Существует по крайней мере три движения - прецессия, нутация и движения полюса Земли. Если первые два движения являются детеминированными и могут быть предсказаны с высокой степенью точности, то третье движение - движение полюса - является стохастическим. Независимо от природы этих движений они эквивалентны вращениям на некоторые углы Эйлера. Рассмотрим как это можно сделать.
Оси декартовой системы координат в некоторую текущую эпоху ![]() наблюдений
можно определить через повороты осей той же декартовой системы координат по
отношению к осям в другую эпоху соответствующую началу отсчета как
наблюдений
можно определить через повороты осей той же декартовой системы координат по
отношению к осям в другую эпоху соответствующую началу отсчета как
Здесь мы написали только матрицы соответствующие нутации ![]() и
прецессии
и
прецессии ![]() . Вектора
. Вектора ![]() и
и ![]() обозначают
единичные вектора в эпохи
обозначают
единичные вектора в эпохи ![]() и
и ![]() соответственно. По соглашению в
астрономии первый вектор
соответственно. По соглашению в
астрономии первый вектор ![]() называют средним вектором (в
эпоху
называют средним вектором (в
эпоху ![]() ), а второй -
), а второй - ![]() истинным единичным вектором в эпоху
истинным единичным вектором в эпоху
![]() . Эти определения "средний" и "истинный" используют также и для других
астрономических терминов, определяя таким образом положения звезд, орты
систем координат, небесный экватор, положение точки весеннего
равноденствия, полюс и т.п.
. Эти определения "средний" и "истинный" используют также и для других
астрономических терминов, определяя таким образом положения звезд, орты
систем координат, небесный экватор, положение точки весеннего
равноденствия, полюс и т.п.
Матрица прецессии ![]() в уравнении (1.10) представляет вращение
за счет общей прецессии за период времени
в уравнении (1.10) представляет вращение
за счет общей прецессии за период времени ![]() . Для правых
экваториальных систем координат (первая ось направлена в точку весеннего
равноденствия, третья ось перпендикулярна небесному экватору) вращение
определяется тремя последовательными поворотами:
. Для правых
экваториальных систем координат (первая ось направлена в точку весеннего
равноденствия, третья ось перпендикулярна небесному экватору) вращение
определяется тремя последовательными поворотами:
Здесь матрицы ![]() являются вращениями вокруг оси
являются вращениями вокруг оси ![]() , так что
, так что
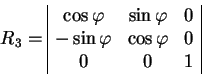 |
(1.12) |
отметим, что по сравнению с математическим определением угла Эйлера
![]() поворот здесь выбран в другую сторону.
поворот здесь выбран в другую сторону.
Отметим также поворот ![]() осуществляется не вокруг оси оси
осуществляется не вокруг оси оси ![]() , а вокруг
оси
, а вокруг
оси ![]() :
:
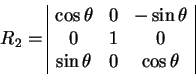 |
(1.13) |
Углы ![]() ,
, ![]() ,
, ![]() являются функциями времени, они
представляются в виде многочленов [1]:
являются функциями времени, они
представляются в виде многочленов [1]:
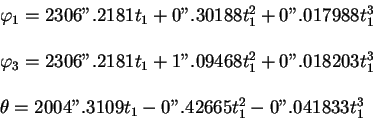 |
(1.14) |
Здесь ![]() - J2000.0 выражено в юлианских столетиях временной шкалы TDB
(аббревиатура TDB означает динамическое барицентрическое время, поодробнее об
определении различных сиистем времени в астрономии можно будет прочитать
в книге В.Е.Жарова).
- J2000.0 выражено в юлианских столетиях временной шкалы TDB
(аббревиатура TDB означает динамическое барицентрическое время, поодробнее об
определении различных сиистем времени в астрономии можно будет прочитать
в книге В.Е.Жарова).
Матрица ![]() представляет вращение обусловленное нутацией. Для
экваториальной системы координат она задается следущим уравнением:
представляет вращение обусловленное нутацией. Для
экваториальной системы координат она задается следущим уравнением:
где ![]() - средний наклон эклиптики,
- средний наклон эклиптики,
![]() ,
,
![]() - компоненты нутации по наклону и долготе. Наклон эклиптики
к экватору
- компоненты нутации по наклону и долготе. Наклон эклиптики
к экватору ![]() является функцией времени и вычисляется в виде
многочлена.
является функцией времени и вычисляется в виде
многочлена.
Для преобразования координат от декартовой системы к экваториальной системе
координат можно использовать, например, уравнение для единичного вектора
указывающего направление на небесный источник:
Мы сделали только преобразование от средней системы координат к истинной
экваториальной системе координат. Необходимо также сделать преобразование
от истинной экваториальной системы координат к земной системе координат, в
которой, собственно, и ведутся наблюдения. Для этого придется сделать
преобразование вида:
здесь ![]() - матрица описывающее суточное вращение Земли, в которую,
кстати, входит и движение полюса, а
- матрица описывающее суточное вращение Земли, в которую,
кстати, входит и движение полюса, а ![]() единичный вектор земной
системы координат. Матрица
единичный вектор земной
системы координат. Матрица ![]() задается в виде произведения трех
матриц - две из которых описывают движение полюса, а третья определяется
часовым углом истинного весеннего равноденствия, которое отсчитывается от
Гринвичского меридиана, этот часовой угол называется также истинным
Гринвичским звездным временем (GAST). Параметры движения полюса
отсчитываются относительно одной из осей условной земной системы координат.
задается в виде произведения трех
матриц - две из которых описывают движение полюса, а третья определяется
часовым углом истинного весеннего равноденствия, которое отсчитывается от
Гринвичского меридиана, этот часовой угол называется также истинным
Гринвичским звездным временем (GAST). Параметры движения полюса
отсчитываются относительно одной из осей условной земной системы координат.
Преобразования типа (1.10, 1.11, 1.15) определяют преобразования координат звезд от положений указанных в каталогах, на момент времени наблюдений. Как видно из приведенных уравнений, для высокоточных наблюдений типа РСДБ - наблюдений, приведение источников на место согласно уравнениям (1.10, 1.11, 1.15) является необходимым условием для успешных наблюдений, поскольку разница от эпохи один год уже приводит к значительному уходу небесного источника от положения указанного в таблиицах. Причем в случае РСДБ наблюдений производится редукция от земной системы координат к небесной системе.
Такие преобразования являются первым шагом на пути редукции небесных источников на истинное положение. Здесь они приведены для полноты. В дальнейшем приведение на истинное положение (редукция) будет обобщена на случай учета релятивистских поправок, которые изменять тривиальные уравнения типа (1.10, 1.11, 1.15).
1.2 Трудности классической механики при описании распространения света
Принцип относительности Галилея сыграл большую роль в создании механики как точной науки.
Физика развивалась, после механики были открыты законы оптики и создана теория электромагнитного поля. Был экспериментально открыт факт, что скорость света - самого быстрого движения в нашем мире не зависит от скорости движения источника света.
Этот факт явно противоречил закону сложения скоростей и принципу относительности Галилея. Более того, принцип относительности Галилея противоречил уравнениям электродинамики и электромагнитного поля.
Основная трудность, которую надо было преодолет путем применения принципа относительности к электродинамике, заключалась в том, что надо было согласовать два противоречящих друг другу утверждения:
- Согласно классической механике скорость любого тела относительно двух
наблюдателей двигающихся относительно друг друга разная.
- Скорость света, согласно опыту, не зависит от движения наблюдателя или источника света и является мировой физической постоянной.
Первое утверждение носило теоретический, концептуальный характер, тогда как второе было основано на опыте. Поскольку второе утверждение основано на опыте, то его ценность выше и следует отказаться отпервого утверждения и тем самым от тех представлений о пространстве и времени, которые были приняты ранее.
Одно из представлений от которых мы отказываемся - ньютоновское понятие одновременности. Ньютон, постулируя существование абсолютного времени, или абсолютной длительности, писал: "время течет всегда одинаково, безотносительно к чему либо внешнему".
В 1905 г. А.Эйнштейном был сформулирован принцип специальной относительности, который был справедлив для применения к теории электродинамики и теории электромагнитного поля и заложил новый взгляд на пространство и время.
1.3 Специальная теория относительности
В специальной теории относительности появляется новое определение понятия одновременности.
Одновременность событий. Два события происходят в один и тот же
момент времени синхронизированных часов в различных точках пространства.
Возникает новое определение синхронизованных часов. Пусть в точках ![]() и
и
![]() есть часы. Определяем, что время прохождения света из
есть часы. Определяем, что время прохождения света из ![]() в
в ![]() равно
времени прохождения света из
равно
времени прохождения света из ![]() в
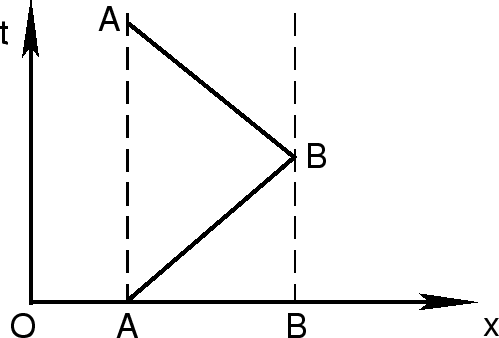
в ![]() . Поясним это на рис. 1.3.
Пусть в момент времени
. Поясним это на рис. 1.3.
Пусть в момент времени ![]() из
из ![]() посылается световой сигнал, он
достигает точки
посылается световой сигнал, он
достигает точки ![]() в момент времени
в момент времени ![]() , отражается и достигает точки
, отражается и достигает точки
![]() в момент времени
в момент времени ![]() . Часы по определению идут в точках
. Часы по определению идут в точках ![]() и
и ![]() синхронно если
синхронно если
| (1.18) |
Принимаются также две аксиомы:
- Если часы
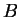 идут синхронно с часами
идут синхронно с часами 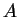 , то часы
, то часы 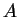 идут синхронно
с часами
идут синхронно
с часами 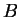 .
.
- Если часы
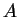 идут синхронно с часами
идут синхронно с часами 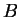 , а часы
, а часы 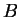 идут синхронно
с часами
идут синхронно
с часами 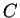 , то часы
, то часы 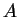 идут синхронно с часами
идут синхронно с часами 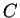 .
.
А.Эйнштейн также сформулировал два принципа: принцип относительности и принцип постоянства скорости света.
Принцип относительности
Законы, по которым изменяются состояния физических систем, не зависят от
того, к которой из двух координатных систем, движущихся друг относительно
друга прямолинейно и равномерно, эти изменения относятся.
Принцип постоянства скорости света
Каждый луч света движется в избранной системе координат со скоростью ![]() ,
независимо от того, испускается ли этот луч покоящимся или движущимся
телом. При этом скорость луча света определяется согласно:
,
независимо от того, испускается ли этот луч покоящимся или движущимся
телом. При этом скорость луча света определяется согласно:
Несмотря на абстрактность эти определения особенно важны для интерпретации астрономических наблюдений. Продемонстрируем это утверждение на простом примере.
1.3.1 Сверхсветовые движения и их интерпретация
Некоторое время назад он представлял из себя загадку для сообщества астрономов, которая бросила вызов теории относительности.
Рассмотрим рис. 1.4. Пусть из источника ![]() выбрасывается
материя (например, сгустки плазмы). Эти сгустки летят под углом
выбрасывается
материя (например, сгустки плазмы). Эти сгустки летят под углом ![]() к
направлению на наблюдателя. Чему равна видимая поперечная скорость
перемещения этих сгустков по небу?
к
направлению на наблюдателя. Чему равна видимая поперечная скорость
перемещения этих сгустков по небу?
Эта задача возникла при анализе т.н. сверхсветовых движений в квазарах. Из многих квазаров наблюдаются выбросы большого количества вещества. При наблюдениях выбросов астрономы измеряли их угловые скорости. По их красному смещению определялось расстояние до квазаров. Умножая расстояние до квазаров на угловую скорость перемещения выбросов по небу астрономы получали поперечную скорость движения выброса. Стандартная процедура дала неожиданный результат. В нескольких случаях поперечная скорость движения выбросов оказалась больше скорости света!
Астрономы были поставлены перед нелегкой задачей. Казалось, что надо сделать выбор из двух, одинаково плохих вариантов. Первый - признать, что в природе могут существовать скорости больше, чем скорость света. Просто они не встречаются ни в солнечной системе, ни тем более в лабораторных условиях. Второй вариант - признать, что красное смещение в квазарах - не результат космологического красного смещения, а следовательно квазары могут быть расположены к нам гораздо ближе. Оба варианта, как я уже сказал были плохими.
Однако, решение задачи оказалось возможным в рамках как специальной теории относительности, так и в рамках космологического сценария существования квазаров. Решение, найденное П.Шейером, основывалось на правильном обращении с понятием одновременности.
Рассмотрим движение одного сгустка вещества. Пусть в момент времени ![]() он выбрасывается из источника
он выбрасывается из источника ![]() под углом
под углом ![]() к направлению
к направлению ![]() .
Сгусток представляет из себя плазму, излучающую радиоволны. Поэтому
одновременно с выбросом сгустка, к наблюдателю по направлению
.
Сгусток представляет из себя плазму, излучающую радиоволны. Поэтому
одновременно с выбросом сгустка, к наблюдателю по направлению ![]() идет
световой сигнал (фотоны радиочастоты) о том, что сгусток выброшен. Сгусток
движется со скоростью
идет
световой сигнал (фотоны радиочастоты) о том, что сгусток выброшен. Сгусток
движется со скоростью ![]() и через некоторый интервал времени
и через некоторый интервал времени ![]() оказывается в положении
оказывается в положении ![]() . К этому времени световой сигнал прошел путь
. К этому времени световой сигнал прошел путь
![]() и оказался в точке
и оказался в точке ![]() . Сгусток продолжает излучать радиофотоны.
Поэтому через время
. Сгусток продолжает излучать радиофотоны.
Поэтому через время ![]() из точки
из точки ![]() в направлении наблюдателя вновь идет
сигнал о том, что сгусток достиг
в направлении наблюдателя вновь идет
сигнал о том, что сгусток достиг ![]() . Построим вспомогательный
перпендикуляр из
. Построим вспомогательный
перпендикуляр из ![]() на прямую соединяющую
на прямую соединяющую ![]() и
и ![]() . Вычислим
продольное расстояние
. Вычислим
продольное расстояние ![]() между точками
между точками ![]() и
и ![]() . Оно
равняется:
. Оно
равняется:
Поперечное расстояние между точками ![]() и
и ![]() равняется величине:
равняется величине:
Угол между прямыми ![]() и
и ![]() ничтожно мал (мы считаем, что расстояние до
квазара значительно превосходит все остальные масштабы рассматриваемой
задачи). Поэтому сигналы о том, что сгусток вышел из источника
ничтожно мал (мы считаем, что расстояние до
квазара значительно превосходит все остальные масштабы рассматриваемой
задачи). Поэтому сигналы о том, что сгусток вышел из источника ![]() и пришел
в точку
и пришел
в точку ![]() придут к наблюдателю через интервал времени
придут к наблюдателю через интервал времени
![]() , а поперечное расстояние пройденное этим сгустком будет составлять
, а поперечное расстояние пройденное этим сгустком будет составлять
![]() . Теперь можно разделить поперечное расстояние
на интервал времени
между событие 1 (выход сгустка из источника) и событием 2 (появление
сгустка в точке
. Теперь можно разделить поперечное расстояние
на интервал времени
между событие 1 (выход сгустка из источника) и событием 2 (появление
сгустка в точке ![]() ) получаем видимую скорость перемещения сгустка по небу:
) получаем видимую скорость перемещения сгустка по небу:
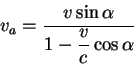
Отсюдя видно, что когда скорость движения сгустка близка к скорости света,
а угол ![]() мал, видимая скорость движения сгустка по небу может
значительно превышать скорость света.
мал, видимая скорость движения сгустка по небу может
значительно превышать скорость света.
Рассмотрим подробнее условия при которых видимая скорость перемещения
сгустка по небу будет превышать скорость света. Итак, будем считать, что
Поскольку тригонометрические функции не превышают 1, то появляется первое условие для скорости сгустка
Значит, когда угол ![]() находится в пределах 0
находится в пределах 0 ![]()
![]() наблюдатель видит сверхсветовое перемещение сгустка по небу.
наблюдатель видит сверхсветовое перемещение сгустка по небу.
В этом примере сверхсветовое движение было объяснено без выхода за рамки специальной теории относительности. Здесь основную роль сыграло правильное обращение с понятием одновременных событий ( в данном случае одновременный приход сигналов к наблюдателю).
<< Введение | Оглавление | 2. Специальная теория относительности >>