Астронет > Footnotes

Астронет: М. В. Сажин/ГАИШ Теория относительности для астрономов
http://variable-stars.ru/db/msg/1170927/footnode.html

Теория относительности для астрономов

... Эйлера ^1.1 Так в математике называются параметры группы вращения, в честь знаменитого российского ученого, члена императорской академии наук Л.Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...\space ^1.2 В астроономии поворот чаще обозначают 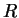, но математики предпочитают греческие буквы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... координат ^1.3 Более подробно об этом можно будет прочитать в книге В.Е.Жарова, которая выходит в этой же серии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... ICRF ^1.4 International Celestial Refrence Frame или международная небесная система отсчета, в дальнейшем при ссылках на эту систему будем называют ее международной аббревиатурой ICRF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... вида ^2.1 Линейность преобразований следует из того факта, что в пределе малых скоростей искомые преобразования должны сводиться к преобразованиям Галилея и они должна описывать преобразования между двумя равномерно и прямолинейно движущимися системами координат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... матрица ^2.2 Кронекер - немецкий математик 19 века, знаменитый своим изречением "Бог создал целые числа; все остальное дело рук человека". По иронии судьбы был учителем Георга Кантора - немецкого математика, родившегося в России, который обосновал существование иррациональных, трансцендентных и трансфинитных чисел в математике . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... жизни ^3.1 Подчеркивание добавлено при переводе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... состояния ^3.2 Конечно в таком рассуждении мы пренебрегаем сопротивлением воздуха . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... единице ^6.1 Рассмотрение нулевой геодезической приводит, разумеется к такому же результату. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... меняются ^6.2 Скалярное поле, разумеется может меняться от точки к точке. Но компонента скалярного поля при параллельном переносе из точки в точку остается неизменной. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... вектором ^6.3 Такие вектора в математике называются инфинитезимальными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... Римана ^7.1 Риман - знаменитый немецкий математик, один из трех общепризнанных создателей неэвклидовой геометрии. Считается, что неэвклидову геометрию создал Н.Лобачевский - математик, ректор Казанского университета. Независимо от Лобачевского геометрию не содержащую постулата о параллельных прямых создал венгерский математик Я. Бойияи. К.Риман - третий в этом списке, он первый исследовал геометрию положительной кривизны. Двумерный образ такой неэвклидовой геометрии - поверхность сферы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... т.п.^9.1 Это следует из требования положительной определенности энергии. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... величина ^9.2 Напомним, что интеграл от скалярной плотности является скалярной величиной. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .