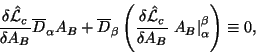|
Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения http://www.astronet.ru/db/msg/1170672/node5.html |
- 1.3.1 Обобщенный ток
- 1.3.2 Обобщенный суперпотенциал
- 1.3.3 Вклад от дивергенции в лагранжиане
- 1.3.4 Неопределенность и единственность в определении токов и суперпотенциалов
- 1.3.5 Единственность токов и суперпотенциалов в определении КБЛ
1.3 Построение сохраняющихся токов и суперпотенциалов на произвольном вспомогательном фоне. Проблема единственности
Рассмотрим произвольную ковариантную теорию с лагранжианом [20]
(сначала он в неявно ковариантном виде):
![]() ,
где AB -- это набор динамических переменных,
произвольных тензорных плотностей.
Внешнее заданное фоновое пространство-время введем простой
тождественной заменой:
,
где AB -- это набор динамических переменных,
произвольных тензорных плотностей.
Внешнее заданное фоновое пространство-время введем простой
тождественной заменой:
![]() .
Тогда лагранжиан перепишется в явно ковариантной форме:
.
Тогда лагранжиан перепишется в явно ковариантной форме:
Поскольку лагранжиан (1.36) -- это скалярная плотность, составляем для него тождество Нетер:
где коэффициенты однозначно определены лагранжианом следующим образом:
1.3.1 Обобщенный ток
Подробный анализ (1.38) дает другое сильное тождество:
Выражение под дивергенцией в этом тождестве вполне может быть интерпретировано как обобщенный ток:
а само тождество Нетер (1.43) переписывается в виде:
1.3.2 Обобщенный суперпотенциал
Перепишем тождество (1.43) в виде:
Сама форма тождества (1.45) говорит о том, что обобщенный ток должен выражаться в виде:
где суперпотенциал в правой части тождественно удовлетворяет:
Учет третьего из тождеств (1.47) говорит, что суперпотенциал (1.49) явно антисимметричен.
1.3.3 Вклад от дивергенции в лагранжиане
Простым, но очень важным является вопрос
о вкладе в ток и суперпотенцил от дивергенции в лагранжиане.
Ответ был дан еще Кацем [14]. Здесь мы кратко даем
результат.
Поскольку
![]() также является скалярной
плотностью, то для этой добавки отдельно выполняется тождество Нетер:
также является скалярной
плотностью, то для этой добавки отдельно выполняется тождество Нетер:
![]() ,
простой анализ которого приводит к добавкам в коэффициентах
(1.39) - (1.41) и в суперпотенциале (1.49):
,
простой анализ которого приводит к добавкам в коэффициентах
(1.39) - (1.41) и в суперпотенциале (1.49):
Необходимо отметить, что форма этих добавок никак не зависит от структуры векторной плотности
1.3.4 Неопределенность и единственность в определении токов и суперпотенциалов
Хорошо известно, что без изменения тождества (1.45)
к току ![]() может быть добавлена произвольная величина
может быть добавлена произвольная величина
![]() , лишь бы дивергенция от нее
тождественно обращалась в нуль:
, лишь бы дивергенция от нее
тождественно обращалась в нуль:
![]() .
Однако, ,,испорченный'' ток тем же самым способом
может быть ,,исправлен''. Величина
.
Однако, ,,испорченный'' ток тем же самым способом
может быть ,,исправлен''. Величина
![]() не связана с лагранжианом и процедурой Нетер.
С другой стороны, в определении
(1.44) все коэффиценты (1.39) - (1.41)
строго определены лагранжианом,
заданным в общей (неявной) форме. В формуле (1.44) нет ни одного члена
дивергенция от которого явно бы обращалась в нуль.
Тождество (1.45) выполняется как все выражение в целом,
как и должно быть для единого сохраняющегося тока Нетер.
Таким образом, можно сделать утверждение:
не связана с лагранжианом и процедурой Нетер.
С другой стороны, в определении
(1.44) все коэффиценты (1.39) - (1.41)
строго определены лагранжианом,
заданным в общей (неявной) форме. В формуле (1.44) нет ни одного члена
дивергенция от которого явно бы обращалась в нуль.
Тождество (1.45) выполняется как все выражение в целом,
как и должно быть для единого сохраняющегося тока Нетер.
Таким образом, можно сделать утверждение:
- Ток (1.44) --
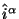 -- в смысле процедуры Нетер
определяется единственнным образом лагранжианом теории.
-- в смысле процедуры Нетер
определяется единственнным образом лагранжианом теории.
Подобные выводы справедливы и для определения суперпотенциала
(1.49). В принципе, без изменения тока ![]() к суперпотенциалу
в (1.48) может быть добавлена произвольная величина
к суперпотенциалу
в (1.48) может быть добавлена произвольная величина
![]() ,
лишь бы дивергенция от нее
тождественно обращалась в нуль:
,
лишь бы дивергенция от нее
тождественно обращалась в нуль:
![]() .
Однако, эта добавка никак не связана с лагранжианом и процедурой Нетер.
Как ее добавили, точно также легко уничтожить.
С другой стороны, в определении (1.49) все члены строго
определены лагранжианом и описанной процедурой --
их невозможно откинуть. Поэтому мы делаем утверждение:
.
Однако, эта добавка никак не связана с лагранжианом и процедурой Нетер.
Как ее добавили, точно также легко уничтожить.
С другой стороны, в определении (1.49) все члены строго
определены лагранжианом и описанной процедурой --
их невозможно откинуть. Поэтому мы делаем утверждение:
- Суперпотенциал (1.49) --
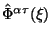 --
в смысле процедуры Нетер
определяется единственнным образом лагранжианом теории.
--
в смысле процедуры Нетер
определяется единственнным образом лагранжианом теории.
Сделав это утверждение, мы, кроме того, проиллюстрируем, что
двусмысленность в суперпотенциале не опасна, во всяком
случае для построения глобальных
сохраняющихся величин.
Так, тождество
![]() в свою очередь говорит о том, что добавка должна быть выражена как
в свою очередь говорит о том, что добавка должна быть выражена как
![]() , где
, где
![]() .
Сочетание требования ковариантности и необходимости использовать
частные производные для построения законов сохранения и глобальных величин
приводит к тому, что величина
.
Сочетание требования ковариантности и необходимости использовать
частные производные для построения законов сохранения и глобальных величин
приводит к тому, что величина
![]() , то есть
должна быть антисимметрична по всем
индексам. Теперь перепишем закон сохранения (1.48) в измененном виде:
, то есть
должна быть антисимметрична по всем
индексам. Теперь перепишем закон сохранения (1.48) в измененном виде:
что дает возможность построить сохраняющиеся величины аналогично (1.30):
![$\displaystyle {\cal P}(\xi) =
\int_{\Sigma} \hat i^0(\xi)d^3 x =
\oint_{\partia...
...[\hat \Phi^{[0n]}(\xi)+
\partial_m \left(\hat j^{[0nm]}(\xi)\right)\right]ds_n.$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img149.gif) |
В силу теремы Стокса последний член не дает вклада в интеграл и, таким образом, не изменяет величину
1.3.5 Единственность токов и суперпотенциалов в определении КБЛ
Вернемся к вопросу b) в конце предыдущей части о единственности
величин в определении КБЛ. Прежде всего обсудим лагранжиан (1.27).
Перепишем скалярную кривизну в явно ,,ковариантизованном'' виде:
где, напомним,
![]() и
и
![]() .
.
С учетом того, что мы знаем какой вклад дают дивергенции (см. (1.50)), лагранжиан (1.27) является как раз того вида, что и лагранжиан (1.36) в этой части. Следовательно, лагранжиан (1.27) может быть подставлен в общие формулы этой части. Прямая подстановка показывает, что все формулы КБЛ получаются этим путем. Так, подстановка (1.27) в обобщенный ток (1.44) дает КБЛ ток (1.32). Более детально: Подстановка в коэффициент (1.39) и учет уравнений Эйнштейна дает тензор энергии-импульса (1.33). Подстановка в (1.40) дает спиновый коэффициент (1.35). Подстановка в (1.41) дает точно Z-член в (1.32). (Необходимо только учитывать разницу знаков в формулах (1.39) - (1.41) и в определении тока (1.44).) Такое же соответствие и между суперпотенциалами: (1.49) переходит точно в (1.31). Из сказанного остается сделать вывод:
- Результаты КБЛ определены однозначно в смысле процедуры Нетер лагранжианом модели (1.27).
<< 1.2 Суперпотенциал Каца-Крушциела ... | Оглавление | Литература к лекции 1 >>
![$\displaystyle \left[{{\delta {\hat{\cal L}}_c} \over {\delta A_B}} \overline D_...
...} \over {\delta A_B}} \left.A_B\right\vert^\beta_\alpha\right)\right]\xi^\alpha$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img106.gif)
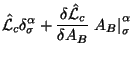
![$\displaystyle \left[{{\partial {\hat{\cal L}}_c} \over {\partial (\overline D_\...
...ine D_\beta \overline D_\alpha A_{B})}}\right) \right]
\overline D_\sigma A_{B}$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img111.gif)
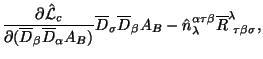
![$\displaystyle \left[{{\partial {\hat{\cal L}}_c} \over {\partial (\overline D_\...
...ta \overline D_\alpha A_{B})}}\right)\right]
\left.A_{B}\right\vert^\tau_\sigma$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img114.gif)
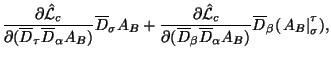
![\begin{displaymath}
\hat n^{\alpha\tau\beta}_\sigma \equiv
{\textstyle{\frac{1}{...
...D_\alpha A_{B})}}
\left.A_{B}\right\vert^\beta_\sigma\right].
\end{displaymath}](http://images.astronet.ru/pubd/2001/09/12/0001170672/img116.gif)