 |
Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения http://www.astronet.ru/db/msg/1170672/node3.html |
- 1.1.1 Псевдотензор Эйнштейна
- 1.1.2 Суперпотенциал Толмена
- 1.1.3 Суперпотенциал Фрейда
- 1.1.4 Вопрос единственности и процедура Нетер
- 1.1.5 Суперпотенциал Моллера
- 1.1.6 Нековариантность псевдотензоров и соответствующие проблемы
- 1.1.7 Ковариантизация псевдотензоров и корректные законы сохранения
1.1 Классические псевдотензоры и суперпотенциалы: краткая история, некоторые свойства и проблемы
1.1.1 Псевдотензор Эйнштейна
Рассматривая проблему энергии гравитационного поля и, в частности,
гравитационных волн, Эйнштейн [1] впервые для построения законов
сохранения в ОТО предложил псевдотензор энергии-импульса
гравитационного поля. Он конструируется следуя определению
канонического тензора энергии-импульса в обычной полевой теории.
Вместо ковариантного лагранжиана используется так называемый усеченный
нековариантный лагранжиан Эйнштейна:
Это и есть псевдотензор Эйнштейна. Из анализа лагранжиана (1.1) следует дифференциальный закон сохранения
который, собственно, является уравнением непрерывности:
где латинские индексы отвечают пространственным координатам k = 1, 2, 3.
1.1.2 Суперпотенциал Толмена
Закон сохранения (1.3) выполняется при выполненных
уравнениях Эйнштейна в вакууме. Это означает, что при
Обычно суперпотенциалом называют величину, двойная дивергенция которой тождественно обращается в нуль. Суперпотенциал
Для невакуумного случая тождество (1.6) переходит в тождество
которое при выполненных уравнениях Эйнштейна переходит в уравнение
Фактически это другая форма уравнений Эйнштейна. Из (1.9) несложно видеть, что для невакуумных решений ОТО вместо (1.3) нужно использовать дифференциальный закон сохранения:
1.1.3 Суперпотенциал Фрейда
Как правило, в качестве суперпотенциалов
используют антисимметричные величины, так что становится
очевидным тождественное равенство нулю двойной дивергенции от них.
Суперпотенциал Толмена (1.7)
не обладает этим свойством. В результате
возникают неудобства при использовании, сложности при ковариантизации.
Улучшить ситуацию удалось Фрейду [3]. Зараннее предполагая антисимметрию
суперпотенциала
![]() ,
соответствующего эйнштейновскому псевдотензору,
вместо уравнения (1.9) он предложил
,
соответствующего эйнштейновскому псевдотензору,
вместо уравнения (1.9) он предложил
Казалось бы существует противоречие между (1.9) и (1.11). В действительности оно видимое, поскольку
1.1.4 Вопрос единственности и процедура Нетер
Даже имея в распоряжении вполне определенный
псевдотензор мы только что убедились в неопределенности
построения суперпотенциалов. Рассмотрим проблему единственности
законов сохранения, таких как (1.3) или (1.10), подробнее.
Используя метрику и ее первые
производные построим произвольным
образом величину
![]() , потребуем только, чтобы она
удовлетворяла тождеству
, потребуем только, чтобы она
удовлетворяла тождеству
![]() .
Затем определим величину
.
Затем определим величину
где
Такая неопределенность в законах сохранения не может быть
удовлетворительной. Однако формула (1.2) указывает, что определение
псевдотензора, в принципе, могло бы быть связано с выбором лагранжиана.
Исследование этой проблемы было проведено детально, ей уделили внимание такие
авторы как Бергман [4], Голдберг [5], Моллер [6],
Траутман [7], Мицкевич [8].
Кратко результаты этих усилий сводятся к следующему.
Несмотря на то, что лагранжиан (1.1) не является общековариантным, --
он инвариантен относительно линейных пребразований.
Это позволяет для трансляций определенных вектором
![]() написать тождество Нетер:
написать тождество Нетер:
который при использовании уравнений Эйнштейна дает закон сохранения (1.10). Таким образом:
- В смысле процедуры Нетер, эйнштейновский псевдотензор (1.2) единственно определяется эйнштейновским лагранжианом (1.1).
- Если лагранжианы различаются на
дивергенцию:
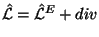 , то они (хотя и приводят к
одним и тем же уравнениям движения) дают различные
псевдотензоры.
, то они (хотя и приводят к
одним и тем же уравнениям движения) дают различные
псевдотензоры.
1.1.5 Суперпотенциал Моллера
Таким образом, свобода в выборе псевдотензора в принципе
не ограничивается -- она переходит в свободу выбора лагранжиана.
То есть так или иначе, чтобы получить определенный результат необходимо
использовать дополнительные ,,разумные'' требования при построении
псевдотензоров и суперпотенциалов. Требования Моллера [6]
при построении
его псевдотензора
![]() и суперпотенциала
и суперпотенциала
![]() следующие:
следующие:
- (I) Для изолированных систем 4-импульс всей системы на пространственной
бесконечности
должен преобразовываться как свободный 4-вектор при линейных координатных преобразованиях. - (II)
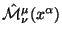 должен алгебраически
зависеть от метрики
должен алгебраически
зависеть от метрики 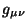 и производных от нее
до второго порядка.
и производных от нее
до второго порядка.
- (III)
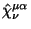 должен быть антисимметричным
по
должен быть антисимметричным
по 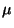 и
и 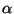 и зависеть от
и зависеть от 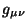 и только ее первых
производных.
и только ее первых
производных.
- (IV) Компоненты
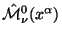 должны преобразовываться как
4-векторная плотность по отношению к чисто пространственным
преобразованиям:
должны преобразовываться как
4-векторная плотность по отношению к чисто пространственным
преобразованиям:
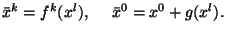
с явной формой суперпотенциала:
Оказалось, что псевдотензор в (1.19) и суперпотенциал (1.20) соответствуют (в смысле процедуры Нетер) ковариантному лагранжиану Гилберта
![]() .
.
1.1.6 Нековариантность псевдотензоров и соответствующие проблемы
Нековариантные величины в физике вообще мало желательны. Однако ОТО занимает особое положение, поскольку простанство-время (в котором происходят взаимодействия) само является динамическим объектом. В силу принципа эквивалентности невозможно построить локальную плотность энергии гравитационного поля. В результате этого и появляются нековариантные псевдотензоры, значения которых в каждой точке могут буть обращены в нуль координатными преобразованиями.
Кроме того, что дифференциальные законы сохранения полезны в локальном смысле (это уравнения непрерывности), они необходимы для построения так называемых глобальных законов сохранения. Если в дифференциальных законах (таких как (1.3), (1.4) или (1.10)) использование псевдотензоров выглядит более или менее естественно, то при построении глобальных законов на некоторые трудности приходится закрывать глаза. Это вынужденный шаг при наличии псевдотензоров, он часто встречается в учебниках, в частности в замечательном учебнике Ландау и Лифшица [9]. Сейчас мы проанализируем ситуацию.
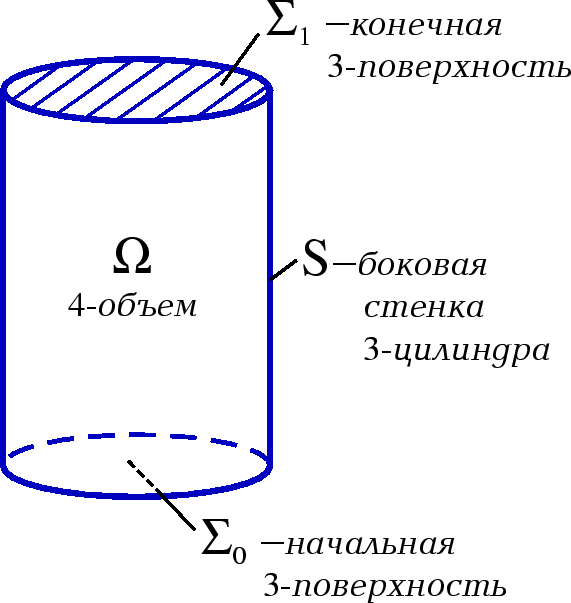
|
| Рис.1. |
В пространстве-времени рассматривается 4-мерный объем ![]() ,
ограниченный цилиндром
с пространственноподобными сечениями
,
ограниченный цилиндром
с пространственноподобными сечениями ![]() и
и ![]() ,
и боковой времениподобной стенкой S (Рис. 1).
Пусть мы имеем в распоряжении дифференциальный закон сохранения для некоторого
псевдотензора
,
и боковой времениподобной стенкой S (Рис. 1).
Пусть мы имеем в распоряжении дифференциальный закон сохранения для некоторого
псевдотензора
![]() :
:
а затем используется обобщенная теорема Гаусса
где для
Если последний интеграл в (1.23) исчезает, то 4-импульс (1.24) сохраняется; если последний интеграл в (1.23) не исчезает, то он определяет поток через боковую стенку цилиндра и
Критика (1.21) - (1.24) очевидна: 1) нельзя интегрировать нековариантные величины, 2) нельзя интегрировать величины с координатными индексами. Однако, несмотря на убийственнность аргументов ситуация может быть спасена.
1.1.7 Ковариантизация псевдотензоров и корректные законы сохранения
Чтобы ковариантизовать псевдотензоры нужно представить,
что существует вспомогательное пространство Минковского, а все
величины записаны в лоренцевых координатах. (Тогда при переходе
к произвольным координатам частные производные естественнным образом
переходят в ковариантные.) Таким образом, нужно считать, что
в нековариантных формулах ,,запрятана'' метрика Минковсого
![]() и ее определитель
и ее определитель
![]() .
.
Замечание: Использование дополнительного заданного пространства-времени в теории, где его фактически не существует, кажется, недопустимым. Однако, очень многие задачи в ОТО, -- как чисто теоретические, так и расчеты экспериментов, -- как раз используют это предположение. Сам характер задач требует использования фона. Конечно внутренняя согласованность ОТО не нарушается -- уравнения Эйнштейна остаются уравнениями Эйнштейна.
Необходимо также избавиться от интегрирования векторных величин.
В обычных полевых теориях сохраняющиеся интегралы соответствуют
симметриям пространстве-времени, в котором эти теории
рассматриваются. Давайте и теперь использовать векторы трансляций
Киллинга
![]() уже введенного вспомогательного пространства Минковского,
где нижний индекс есть лишь
номер вектора Киллинга, это не координатный индекс.
уже введенного вспомогательного пространства Минковского,
где нижний индекс есть лишь
номер вектора Киллинга, это не координатный индекс.
После этих предположений (1.21) переписывается в эквивалентной форме:
где слева, очевидно, скалярная плотность, которая без проблем интегрируется по 4-объему:
![$\displaystyle \int_\Omega
\partial_\mu \left[\sqrt{-\eta} \left({\hat \theta^\mu_\rho} / {\sqrt{-\eta}}\right)
\xi^\rho_{(\nu)}\right] d^4 x = 0,$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img62.gif) |
что приводит к корректному определению 4-импульса на сечении
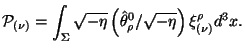 |
Анализируя последние три формулы, можно сделать вывод, что
сам псевдотензор играет лишь вспомогательную роль.
На самом деле ,,дифференциально'' сохраняется
векторная плотность (ток):
<< 1. Теорема Нетер: псевдотензоры ... | Оглавление | 1.2 Суперпотенциал Каца-Крушциела ... >>