Астронет > 5.3 Интерпретация заданного фона в полевой формулировке ОТО

Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://variable-stars.ru/db/msg/1170672/node27.html

<< 5.2 Изолированные системы на ... | Оглавление | 5.4 Проблемы интерпретации решений >>

Разделы

5.3 Интерпретация заданного фона в полевой формулировке ОТО

5.3.1 Ненаблюдаемость фона в полевой формулировке

Как мы уже отмечали, полевая и геометрическая формулировки ОТО -- это разные представления одной и той же теории, они эквивалентны. Наблюдательные предсказания должны быть одними и теми же. В ОТО принципиально нет наблюдаемого фиксированного пространства-времени. Действительно после отождествлений

$\begin{displaymath} \sqrt{-g}g^{\mu\nu} \equiv \hat g^{\mu\nu} \equiv \overline ... ...u\nu}} +\hat l^{\mu\nu}, \Phi^A = \overline \Phi^A + \phi^A \end{displaymath}$

(5.34)

полевая формулировка переходит в геометрическую. Как метрика $\overline { g_{\mu\nu}}$ , так и поля $\overline \Phi^A$ исчезают из рассмотрения. Отождествление (5.34) говорит о том, что фоновые поля не участвуют во взаимодействиях независимо от динамических, таким образом -- это указание, что фоновые поля не наблюдаемы.

Как проследить наглядно (физически) что фон действительно ненаблюдаем (см. подробнее работу [10])? Предположим, что пространство Минковского выбрано в качестве фона. В пространстве Минковского без всякой гравитации световой сигнал движется по прямым, его скорость и частота стабильны. Тем самым метрические свойства фона определяются однозначно стандартными процедурами с использованием света. В присутствии гравитационных полей $\hat l^{\mu\nu}$ скорость световых сигналов и частота изменяется. Тогда измерение расстояний становится сильно зависимым от $\hat l^{\mu\nu}$ , то есть пространство Минковского перестает быть наблюдаемым с помощью световых сигналов.

Оно также перестает быть наблюдаемым, если попытаться определить измерения с помощью гравитационно-волнового сигнала. Рассмотрим полевые уравнения полевой формулировки на плоском фоне

$\begin{displaymath} \hat G^L_{\mu\nu}(l) = \kappa \left( \hat t^{gr}_{\mu\nu} + \hat t^{m}_{\mu\nu}\right) \end{displaymath}$

(5.35)

с левой частью

$\begin{displaymath} 2\hat G^L_{\mu\nu}(l) \equiv \overline D^\alpha_{ \alpha} \h... ...l^\alpha_{ \mu} - \overline D_{\alpha\mu}\hat l^\alpha_{ \nu}. \end{displaymath}$

(5.36)

В необходимой калибровке в левой части (5.35), как видно из (5.36), может остаться лишь оператор Даламбера $\overline D^\alpha_{ \alpha}$ . Тем самым, казалось бы, определение пространства Минковского гарантировано. Но ,,не все карты открыты''! Необходимо учитывать самодействие в правой части (5.35). Среди всех членов там содержатся также члены типа $\sqrt{-\bar g} l^{\alpha\beta} l^{\mu\nu}_{ ,\alpha\beta}$ , которые очевидно искажают даламбертиан пространства Минковского и делают это пространство ненаблюдаемым.

5.3.2 Замкнутая модель Фридмана в терминах полевой формулировки

Здесь, на примере замкнутой Вселенной Фридмана мы покажем, что плоский фон можно использовать в самых казалось бы недопустимых ситуациях, когда топология фонового и физического пространства-времени не совпадают. С одной стороны, мы продемонстрируем условность такого выбора фона, с другой стороны, несмотря на это использование полевой формулировки приводит к вполне осмысленным результатам [11].

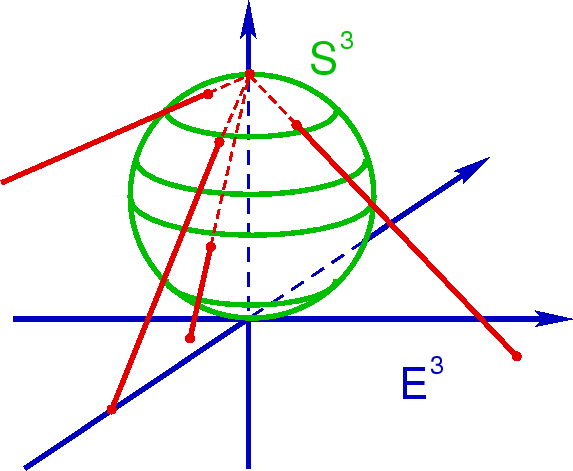
Рис.4. Стереографическая проекция

Метрику замкнутого мира представим в виде:

$\begin{displaymath} ds^2 = - c^2 dt^2 + {a^2 \over {1+r^2/4}} \left(d{x^1}^2 + d{x^2}^2 +d {x^3}^2\right). \end{displaymath}$

(5.37)

Для построения полевой конфигурации выбираем фон как пространство Минковского с лоренцевыми координатами в (5.37) и разбиение: $\hat g^{\mu\nu} = {\eta^{\mu\nu}} + l^{\mu\nu}.$ Тогда ненулевые компоненты полевой конфигурации имеют значения:

$\begin{displaymath} l^{00} = 1 - \left({a^2 \over {1+r^2/4}}\right)^3, l^{11} = l^{22} = l^{33} = {a^2 \over {1+r^2/4}} -1. \end{displaymath}$

(5.38)

Такая конфигурация соответствует так называемой стереографической проекции 3-сферы на плоское 3-пространство (Рис. 4). ,,Нижний'' полюс сферы соответствует началу координат, ,,верхний'' полюс отождествляется сразу со всеми точками на формальной бесконечности плоского мира. Таким образом топология 3-сферы S³ как бы ,,упрощается'' до топологии плоского пространства E³. Поле (5.38) формально запоняет бесконечный объем. Если же производить физически разумные измерения с помощью реальных световых сигналов в гравитационном поле, то придем к стандартному значению объема 3-сферы.

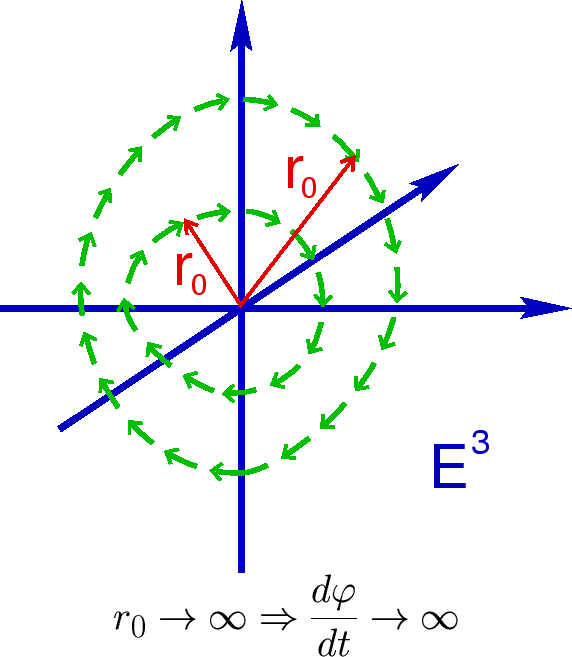
Рис.5.

Условность выбранного фона подчеркивается также следующим мысленным экспериментом. Представьте, что в пространстве Минковского, заполенном полем (5.38) лучи света движутся по окружностям с центром в начале координат (Рис. 5). Свободно свет не может двигаться таким образом, но картина может быть смоделирована с помощью системы зеркал и предельной процедуры. Тогда в сферической системе координат уравнение такой ,,геодезической'' имеет вид

$\displaystyle \theta$	=	$\displaystyle \theta_0 = const,$
r	=	r₀ = const,
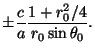$\displaystyle {d\phi \over dt}$	=	$\displaystyle \pm {c\over a} {{1+ r^2_0/4}\over {r_0\sin \theta_0}}.$

Как видно, при $r_0 \rightarrow \infty$ ,,угловая'' скорость света становится бесконечной и для прохождения полной окружности на бесконечности времени совсем не требуется. При возвращении к физическому пространству-времени все становится на свои места, поскольку вся пространственная бесконечность пространства Минковского соответсвует одной единственной точке -- ,,верхнему'' полюсу 3-сферы.

Несмотря на условность плоского фона в рамках замкнутой модели Фридмана, конфигурация (5.38) имеет вполне физическую интерпретацию. Действительно, посчитаем для нее интегралы движения (5.18), определяющие глобальные сохраняющиеся величины в пространстве Минковского. Мы получим все 10 величин равными нулю. Это как раз сооответствует возможному квантовому рождению замкнутого мира из ,,ничего'' [12].

<< 5.2 Изолированные системы на ... | Оглавление | 5.4 Проблемы интерпретации решений >>