 |
Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения http://www.astronet.ru/db/msg/1170672/node26.html |
- 5.2.1 Асимптотически плоское пространство-время
- 5.2.2 Глобальные сохраняющиеся величины
- 5.2.3 Наислабейшее убывание гравитационных потенциалов
5.2 Изолированные системы на пространнственной бесконечности
5.2.1 Асимптотически плоское пространство-время
Мы называем пространство-время
асимптотически плоским, если оно соответствует изолированной (островной)
системе в плоском пространстве-времени (см., например,
работы [4]![]() [5]),
и в качестве определения удовлетворяет следующим исходным
,,наивным'' требованиям:
[5]),
и в качестве определения удовлетворяет следующим исходным
,,наивным'' требованиям:
- (1)
На пространственной бесконечности мировые точки параметризуются
координатами
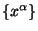 такими, что
такими, что
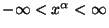 .
.
- (2)
В одной из этих систем метрика имеет поведение:
при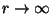 , где
, где
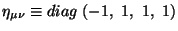 и
и
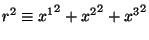 .
Обозначение
.
Обозначение 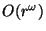 соответствует
асимптотическому поведению при
соответствует
асимптотическому поведению при
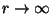 .
.
- (3)
Не существует координатных систем, для которых падение
потенциалов гравитационного поля было бы быстрее, чем в (5.13).
- (4) Тензор энергии-импульса источников в системе (5.13) имеет
поведение:
Переформулируем это определение в рамках полевого подхода. Для этого нужно выбрать фон. Мы выбираем пространство Минковского в лоренцевых координатах (5.13). После выбора фона выбор координат (в силу ковариантности всех выражений полевой формулировки) не важен, но лоренцевы координаты здесь удобны, поскольку в них очевидно асимптотическое поведение. По этой же причине мы не используем крышки в этой части лекции. Итак, пункт (1) сохранится.
- (2)
В одной из калибровок гравитационные потенциалы имеют поведение:
- (3)
Не существует калибровок, где убывание
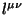 было бы быстрее, чем в (5.15).
было бы быстрее, чем в (5.15).
- (4)
Условие для материальных источников также сохраняется:
5.2.2 Глобальные сохраняющиеся величины
Для того, чтобы определить интегралы движения
островной системы мы используем векторы Киллинга фонового
пространства Минковского:
где сечения
где d Sk элемент координатного объема на ,,стенках'' цилиндра (см. Рис. 1), окружающего изолированную систему.
Уравнения Эйнштейна в полевой формулировке на плоском фоне
могут быть переписаны в виде
(см. (12) в лекции 4):
Подстановка (5.20) и (5.21) в (5.18) и использование антисимметрии
где dsi -- координатный элемент интегрирования на 2-сфере, окружающей изолированную систему.
5.2.3 Наислабейшее убывание гравитационных потенциалов
Подстановка потенциалов с поведением (5.15) в интегралы движения
приводит к тому, что (5.22) оказываются хорошо определенными,
в то время как (5.23) и (5.24)
расходятся. Чтобы избежать этого,
достаточно усилить условия падения до
где (+) и (-) означают четную и нечетную функции по отношению к изменению знака 3-вектора
Условия (5.25) должны быть Пуанкаре инвариантны, поэтому
необходимо потребовать [5]
как это часто требуют при последующих интегрированиях [7].
Для реальной островой системы падение быстрее, чем в
(5.15) (или в (5.25))
невозможно в силу необходимости соответствовать закону Ньютона
в слабополевом приближении. А вот может ли оно быть слабее без изменения
основных интегральных характеристик? Оказывается, что
может [7]![]() [9]
[9]![]() [5].
Чтобы определить условия падения более слабые, чем (5.25)
мы используем
калибровочно инвариантные свойства полевой формулировки [5].
Как мы установили,
уравнения движения калибровочно инвариантны на самих себе. Это означает,
что для плоского фона полный тензор энергии-импульса
при преобразованиях (5.9) преобразуется как:
[5].
Чтобы определить условия падения более слабые, чем (5.25)
мы используем
калибровочно инвариантные свойства полевой формулировки [5].
Как мы установили,
уравнения движения калибровочно инвариантны на самих себе. Это означает,
что для плоского фона полный тензор энергии-импульса
при преобразованиях (5.9) преобразуется как:
Важно отметить, что выражение
![]() инвариантно (в абсолютном смысле, безотносительно к условиям падения)
относительно
инвариантно (в абсолютном смысле, безотносительно к условиям падения)
относительно
что является самым первым членом суммы в (5.27), и, таким образом, больше не рассматривается.
Теперь будем искать ограничения на поведение ![]() .
Используем следующие очевидные требования:
.
Используем следующие очевидные требования:
- (i) Динамические поля
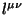 и
и 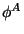 удовлетворяют уравнениям Эйнштейна и условиям падения
(5.16) и (5.25), (5.26).
удовлетворяют уравнениям Эйнштейна и условиям падения
(5.16) и (5.25), (5.26).
- (ii) Каждая из исходных компонент
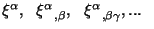 является произвольной независимой величиной в каждой точке пространства
Минковского. Естественна симметрия по нижним индексам.
является произвольной независимой величиной в каждой точке пространства
Минковского. Естественна симметрия по нижним индексам.
- (iii)
Величины
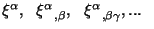 изменяются как тензоры при Пуанкаре преобразованиях.
изменяются как тензоры при Пуанкаре преобразованиях.
- (iv)
Функции
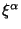 являются класса
являются класса
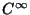 и каждая следующая производная от
и каждая следующая производная от 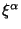 падает быстрее предыдукщей на один порядок по степени
r. Таким образом, все свойства
падает быстрее предыдукщей на один порядок по степени
r. Таким образом, все свойства
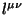 сохраняются для
сохраняются для
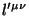 .
.
Предположим условия падения для ![]() в форме:
в форме:
В силу пункта (ii) рассматриваем все члены типа
Этого условия достаточно, чтобы все оставшиеся члены в калибровочной сумме не давали вклада в
Комбинирование (5.30) и (5.31) приводит к ограничениям на поведение (5.28)
которое одновременно гарантирует инвариантность относительно (5.9)
Таким образом, подстановка (5.28) с условиями (5.32)
в (5.9) дает поведение для
гравитационных переменных в виде:
Асимптотика (5.33) с условиями (5.32)
заметно слабее, чем исходная
(5.25). Тем не менее все интегралы (5.18)
(или в явном выражении --
(5.22) - (5.24))
сохраняют свои значения. Мало того, при каждом последующем
калибровочном преобразовании (5.9) с (5.28) и
(5.32):
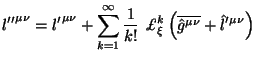 |
мы уже не нарушим поведение (5.33), значения P(K) также остаются прежними.
Наислабейшее асимптотическое поведение (5.33) с условиями
(5.32) являются
новыми результатами, поскольку они
уточняют и исправляют
известные результаты [7]![]() [9].
[9].
<< 5.1 Калибровочные преобразования в ... | Оглавление | 5.3 Интерпретация заданного фона >>
![$\displaystyle {1\over{c \kappa}}?{\lim_{r \rightarrow \infty}}
\int_{\Sigma} \left[ U^{\alpha 0 i}_{????,i}\right] dx^3$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img629.gif)
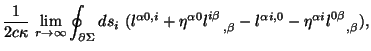
![$\displaystyle {1\over {2 c \kappa}}?{\lim_{r \rightarrow
\infty}} \int_{\Sigma}{ \left [(U^{n0i} x^m - U^{m0i} x^n)_{,i} +
U^{m0n} - U^{n0m} \right]dx^3}$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img632.gif)
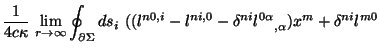
![$\displaystyle {1\over{2 c \kappa}}?{\lim_{r \rightarrow \infty}}
\int_{\Sigma}{
\left[(U^{00i} x^m - U^{m0i} x^0)_{,i} - U^{00m}\right]dx^3}$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img636.gif)
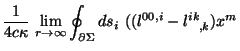
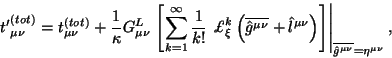
![\begin{displaymath}
O^{-}\left(
\partial_\alpha
\left[\sum^{\infty}_{k = 1}{1\ov...
...at l^{\mu\nu}\right)\right]\right)
< O^{-}\left(r^{-2}\right).
\end{displaymath}](http://images.astronet.ru/pubd/2001/09/12/0001170672/img657.gif)