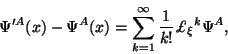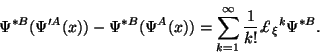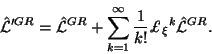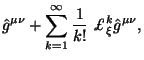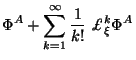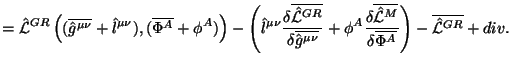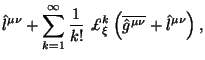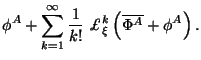Астронет > 5.1 Калибровочные преобразования в полевой формулировке ОТО

Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://variable-stars.ru/db/msg/1170672/node25.html

<< 5. Интерпретация и приложения ... | Оглавление | 5.2 Изолированные системы на ... >>

Разделы

5.1 Калибровочные преобразования в полевой формулировке ОТО

Калибровочные преобразования и их свойства в полевой формулировке прямо вытекают из общей ковариантности ОТО в обычной геометрической формулировке. Подробным образом эта связь исследована в работе [1] с помощью сложной и громоздкой математики. Здесь мы даем ключевые выводы [1] и даем качественные пояснения.

5.1.1 Смещения Ли и преобразования Ли геометрических объектов

Определение преобразований Ли и производных Ли может быть найдено во многих учебниках и с разных позиций, например в работе [2]. Предположим, что некоторое координатное преобразование определено смещением вдоль конгруенции определенной векторным полем $\xi^\alpha$ . Тогда его можно представить в виде ряда

$\begin{displaymath} {x^\prime}^\alpha = x^\alpha + \xi^\alpha (x) + {1\over{2!}}... ...3!}} \xi^\pi (\xi^\beta \xi^\alpha_{ ,\beta})_{,\pi} + {...} \end{displaymath}$

(5.1)

где, вообще говоря, не делается предположений о малости $\xi^\alpha$ и их производных, хотя должны быть введены необходимые предположения о дифференцируемости. Предположим, что на 4-многообразии определен некоторый набор геометрических объектов $\Psi^A(x)$ . После преобразований (5.1) получим $\Psi^A(x) \rightarrow \Psi'^A(x')$ . Теперь сделаем так называемое точечное преобразование, то есть отобразим пространство-время само на себя так что каждой точке со значением координат x в системе { x} сопоставим точку со значением координат x в системе { x'}. После этого сравним геометрические объекты исходного и отображенного пространств. Оказывается, что

$\begin{displaymath} \Psi'^A(x) - \Psi^A(x) = \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k \Psi^A, \end{displaymath}$

(5.2)

где ${\pounds_\xi}$ -- производная Ли, определенная еще в лекции 1.

Предположим, что другой геометрический объект $\Psi^{*B}(\Psi^{A})$ является функцией от набора предыдущих и их производных, и не является явной функцией координат. С одной стороны, в силу определения геометрического объекта на многообразии, после точечного преобразования $\Psi^{*B}$ должен удовлетворять соотношению типа (5.2). С другой стороны, простая подстановка (5.2) в $\Psi^{*B}(\Psi^{A})$ дает тоже самое соотношение:

$\begin{displaymath} \Psi^{*B}(\Psi'^A(x)) - \Psi^{*B}(\Psi^A(x)) = \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k \Psi^{*B}. \end{displaymath}$

(5.3)

5.1.2 Преобразования Ли в геометрической формулировке ОТО

Ковариантные свойства ОТО формально следуют из того, что лагранижиан в действии

$\begin{displaymath} S = {1 \over c} \int d^4x {\hat{\cal L}}^{GR} \equiv -{1 \... ... + {1 \over c} \int d^4x {\hat{\cal L}}^M (\Phi^A, g_{\mu\nu}) \end{displaymath}$

(5.4)

является скалярной плотностью. Являясь геометрическим объектом, лагранжиан в действии (5.4) при точечных преобразованиях изменяется также как в (5.2):

$\begin{displaymath} {\hat{\cal L}}'^{GR} = {\hat{\cal L}}^{GR} + \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k {\hat{\cal L}}^{GR}. \end{displaymath}$

(5.5)

Лагранжиан ${\hat{\cal L}}^{GR}$ не зависит явно от координат, поэтому просто подстановка

$\displaystyle {\hat g}'^{\mu\nu}$	=	$\displaystyle \hat g^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k {\hat g^{\mu\nu}},$
$\displaystyle {\Phi}'^A$	=	$\displaystyle \Phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k {\Phi^A}$	(5.6)

дает тот же результат (5.5). Поскольку ${\hat{\cal L}}^{GR}$ -- скалярная плотность, то любой член в сумме (5.5) является дивергенцией, следовательно, вся сумма также есть дивергенция. Изменение лагранжиана на дивергенцию, как известно, не изменяет результатов варьирования, то есть приведет к тем же самым уравнениям. Поэтому часто при исследовании симметрий действия вместо свойств ковариантности рассматривают инвариантность относительно Ли преобразований. Обычно ограничиваются лишь первым членом в суммах (5.6) и соответственно в (5.5), например, как в учебнике Ландау и Лифшица [3].

5.1.3 Динамический лагранжиан

Давайте перепишем динамический лагранжиан полевой формулировки определенный в (4.25) лекции 4 в конкретной форме:

		$\displaystyle {\hat{\cal L}}^{dyn} = {\hat{\cal L}}^{GR} - {\hat{\cal L}}^{(1)} - {\hat{\cal L}}^{(0)} + div$
		$\displaystyle = {\hat{\cal L}}^{GR}\left((\overline{\hat g^{\mu\nu}} + \hat l^{... ...over {\delta \overline{\Phi^A}}}\right) - \overline{{\hat{\cal L}}^{GR}} + div.$	(5.7)

Обсудим смысл построения. Ясно, что простая подстановка разбиения

$\begin{displaymath} \hat g^{\mu\nu} \equiv \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}, \Phi^A \equiv \overline {\Phi^A} + \phi^A \end{displaymath}$

(5.8)

в ${\hat{\cal L}}^{GR}$ к новым свойствам не приводит. Как при варьировании по динамическим переменным, так и при варьировании по фонововым получаются лишь уравнения Эйнштейна в прежней форме. Решающим является вычитание ${\hat{\cal L}}^{(1)}$ . С одной стороны, варьирование по динамическим переменным дает те же уравнения Эйнштейна. Действительно, член ${\hat{\cal L}}^{(1)}$ не дает вклада поскольку он линееен по $\hat l^{\mu\nu}$ и $\phi^A$ , и пропорционален, как это видно из (5.7), фоновым уравнениям, которые считаются выполненными после варьирования. С другой стороны, благодаря вычитанию ${\hat{\cal L}}^{(1)}$ варьирование ${\hat{\cal L}}^{dyn}$ в (5.7) по фоновой метрике $\overline g^{\mu\nu}$ даст неисчезающий полный тензор энергии-импульса $\hat t^{(tot)}_{\mu\nu}$ (см. (30) в лекции 4) как источник в полевых уравнениях. Вычитание ${\hat{\cal L}}^{(0)}$ также необходимо, действительно, оно гарантирует, что в отсутствие всяких полей ( $\hat l^{\mu\nu}=0$ и $\phi^A=0$ ) отсутствует и сам динамический лагранжиан ${\hat{\cal L}}^{dyn} =0$ .

Остается вопрос, который требует также обсуждения. Почему фоновые уравнения (их операторы входят в ${\hat{\cal L}}^{(1)}$ -- см. (5.7)) мы не считаем выполненными до варьирования? Дело в том, что точно такой же член содержится в первом слагаемом, только неяно. Действительно, ${\hat{\cal L}}^{GR}$ может быть разложен в ряд по динамическим переменным с помощью вариационных производных. Тогда становится очевидным, что ряд содержит ${\hat{\cal L}}^{(1)}$ , но только со знаком (+) и эти члены должны взаимно сокращаться. Такое разложение как раз показывает, что ${\hat{\cal L}}^{dyn}$ не менее, чем квадратичен по $\hat l^{\mu\nu}$ и $\phi^A$ , что естественно для обычной полевой теории.

5.1.4 Калибровочные преобразования

Теперь поясним ту инвариантность, которая была продекларирована в лекции 4 относительно преобразований:

$\displaystyle {\hat l}'^{\mu\nu}$	=	$\displaystyle \hat l^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}\right),$
$\displaystyle {\phi}'^A$	=	$\displaystyle \phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline{\Phi^A}+\phi^A\right).$	(5.9)

Подстановка (5.9) в первый из лагранжианов в (5.7) эквивалентна подстановке (5.6) в ${\hat{\cal L}}^{GR}$ с результатом (5.5), где ланранжиан приобретаеит лишь дополнительную дивергенцию. Подстановка (5.9) в член ${\hat{\cal L}}^{(1)}$ оставляет его пропорциональным фоновым уравнениям. Таким образом, мы доказали утверждение, что ${\hat{\cal L}}^{dyn}$ инвариантен относительно калибровочных преобразований (5.9) с точностью до дивергенций и на фоновых уравнениях.

Инвариантность уравнений движения в полевой формулировке относитель- но (5.9) устанавливается также просто. Полевые уравнения эквивалентны обычным уранениям Эйнштейна на фоновых уравнениях. Значит, с точностью до фоновых уравнений аргументы входят в операторы уравнений только в виде сумм (5.8). А тогда подстановка калибровочных преобразолваний (5.9) в полевые уравнения приведет к преобразованию типа (5.3) для операторов уравнений. А это значит, что если уравнения движения удовлетворены, то они инвариантны относительно (5.9). Другими словами, уравнения движения полевой формулировки ОТО инвариантны относительно калибровочных преобразований (5.9) на самих себе и на фоновых уравнениях.

При преобразованиях (5.9) фоновая метрика не подвергается никаким преобразованиям, координаты тоже неизменны. Значит, (5.9) вполне можно интерпретировать как калибровочные (внутренние) преобразования, и забыть, что они являются результатом смещений Ли в геометрической формулировке и последующего перехода к полевой.

5.1.5 Интепретация калибровочных преобразований

Мы показали как калибровочные преобразования (5.9) в полевой формулировке связаны с преобразованиями Ли в геометрической. Оказывается, что (5.9) также связаны с выбором фона для построения полевой формулировки. Рассмотрим некоторое решение уравнений Эйнштейна $\hat g^{\mu\nu}$ и разобьем его на сумму фоновых и динамических частей:

$\begin{displaymath} \hat g^{\mu\nu}(x) = \overline {\hat g^{\mu\nu}}(x) + \hat l^{\mu\nu}(x). \end{displaymath}$

(5.10)

Сделаем произвольное координатное преобразование, представимое в виде (5.1):

$\begin{displaymath} {x^\prime}^\alpha = {x^\prime}^\alpha (x). \end{displaymath}$

(5.11)

Теперь преобразуем выбранное решение в новые координаты и сделаем разбиение

$\begin{displaymath} (\hat g'^{\mu\nu})(x') = \overline {\hat g^{\mu\nu}}(x') + \hat l'^{\mu\nu}(x'). \end{displaymath}$

(5.12)

Главное свойство этого разбиения в том, что форма фоновой метрики та же самая, что и в разбиении (5.10), хотя и в новых координатах. Теперь в соотношении (5.9) в рамках системы { x'} перейдем от точек со значениями x' к точкам со значениями x. После этого, используя (5.10) и (5.11) в форме (5.1) получим, что $\hat l^{\mu\nu}(x)$ и $\hat l'^{\mu\nu}(x)$ связаны первым из преобразований (5.9).

Рис.3.

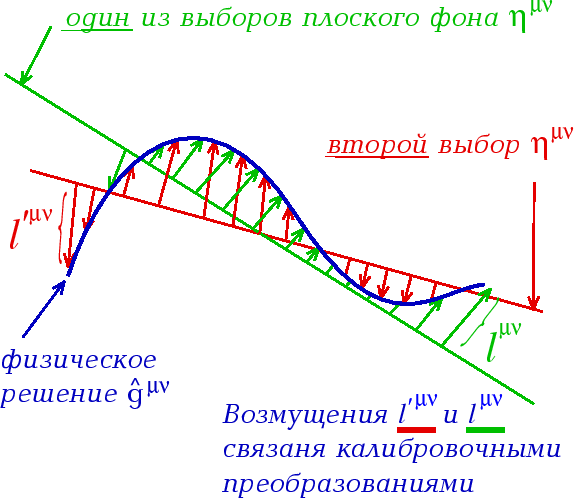
Вспомним, что и в (5.10), и в (5.12) фоновая метрика одна и та же. Но поскольку она выбрана в различных координатах, то это означает что фоновое пространство-время, к которому относится эта метрика, выбирается двумя различными способами. Каждый способ определяет свои возмущения, которые связаны вполне определенными соотношениями (5.9). Качественно эта ситуация поясняется на Рис. 3, где кривая означает само решение, а две прямые означают выбор фона, скажем плоского, двумя различными способами. Отклонения кривой от каждой из прямой определяет два сорта возмущений, которые и связаны калибровочными преобразованиями. Таким образом, фиксация калибровки означает фиксацию способа задания фона.

Как иллюстрацию рассмотрим решение Шварцшильда в двух системах координат: шварцшильдовой $\{ t, R, \theta, \phi\}$ и изотропной $\{ t, \rho, \theta, \phi\}$ . В обоих случаях в качестве фона выберем плоский. В первом случае он описывается сферическими координатами $\{ t, R, \theta, \phi\}$ , во втором случае сферическими координатами $\{ t, \rho, \theta, \phi\}$ . В каждом случае построим возмущения, а затем, скажем в первом случае, заменим R на $\rho$ , тогда получим, что возмущения этих двух сортов связаны преобразованиями типа (5.9), но сейчас без явного выражения через векторы $\xi^\alpha$ .

<< 5. Интерпретация и приложения ... | Оглавление | 5.2 Изолированные системы на ... >>