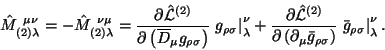|
Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения http://www.astronet.ru/db/msg/1170672/node22.html |
- 4.4.1 Тождество Каца-Бичака-Линден-Белла
- 4.4.2 Тождество Нетер для полевого лагранжиана
- 4.4.3 Суперпотенциал в полевой формулировке ОТО
- 4.4.4 Сравнение результатов метода Нетер-Белинфанте и полевого подхода
- 4.4.5 Разрешение неопределенности Боульвара-Дезера
4.4 Метод Нетер-Белинфанте и полевой подход к ОТО
Комбинация этих двух методов позволяет разрешить описанные в предыдущей части проблемы. Результаты этой части были доложены на семинаре [24].
4.4.1 Тождество Каца-Бичака-Линден-Белла
Напомним как был получен закон сохранения КБЛ [25].
Для лагранжиана
которое затем преобразовано в закон сохранения (см. (1.29) в лекции 1):
Если в процессе преобразований (4.34) не использовать уравнений Эйнштейна и не везде явно представлять
где суперпотенциал как и прежде (см. (31) в лекции 1) имеет вид:
а ток в левой части (4.36) имеет более общий вид, чем в (4.35).
4.4.2 Тождество Нетер для полевого лагранжиана
Гравитационный лагранжиан в полевой формулировке (см. (4.26))
есть
явная форма которого
Теперь используем тождество Нетер
![]() , чтобы преобразовать его к виду:
, чтобы преобразовать его к виду:
где
Вычтем из тождества (4.36) тождество (4.41), учтем равенство
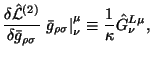 |
связь (4.39), определение (4.42) и получим новое тождество:
представленное в терминах полевого подхода.
4.4.3 Суперпотенциал в полевой формулировке ОТО
Еще раз запишем общее уравнение полевой вормулировки:
где
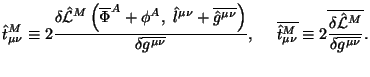 |
Теперь, конечно, источник в (4.45) не является симметричным тензором энергии-импульса, соответствующим динамическому лагранжиану (4.25):
Обсудим это уравнение. Прежде всего, это есть аналог уравнения КБЛ (4.35), здесь в правой части также стоит дивергенция теперь от нового суперпотенциала
Почему этот успех не был достигнут раньше?
Оказывается
было ошибочным
предположение
(для построения сохраняющегося тока
на произвольном
фоне) использовать источник
![]() в правой части
(4.44),
определенный стандартным
образом в (4.30). Оказывается необходимо использовать возмущения
в правой части
(4.44),
определенный стандартным
образом в (4.30). Оказывается необходимо использовать возмущения
![]() . Отметьте также, что в левой части
(4.46)
содержится член взаимодействия с фоном, продекларированный качественно
нами раньше [13]. Z-член в (4.46),
как и везде, обращается в нуль
для векторов Киллинга фона.
. Отметьте также, что в левой части
(4.46)
содержится член взаимодействия с фоном, продекларированный качественно
нами раньше [13]. Z-член в (4.46),
как и везде, обращается в нуль
для векторов Киллинга фона.
4.4.4 Сравнение результатов метода Нетер-Белинфанте и полевого подхода
Главным результатом лекции 2 было построение
закона сохранения (см. (24) в лекции 2):
а суперпотенциал представляет собой сумму КБЛ суперпотенциала и поправки Белинфанте:
Перепишем уравнение (4.46) в компактном виде:
где
Оказывается, что поправка Белинфанте, определенная в (23) в лекции 2
и спиновый член (4.42)
совпадают:
![]() .
Учитывая этот факт в (4.49) и в суперпотенциале в
(4.51), заключаем
.
Учитывая этот факт в (4.49) и в суперпотенциале в
(4.51), заключаем
| = | |||
| = |
и
Таким образом все свойства
- Закон сохранения (4.50) получен в рамках полевого подхода и является точно уравнением (4.47), которое есть следствие метода Нетер-Белин- фанте. Два разных подхода на уровне самых обобщенных законов сохранения дают единый ответ.
Сравнивая тензоры энергии-импульса (4.48) и в (4.51)
находим, что
тензоры
энергии-импульса гравитационного поля не совпадают:
![]() .
(Только для случая, когда
.
(Только для случая, когда
![]() и
и ![]() мы получаем, что должно быть
мы получаем, что должно быть
![]() .)
Тем не менее, с использованием фоновых и динамических
уравнений Эйнштейна равенство (4.52) подтверждается
прямыми расчетами. Такая ситуация говорит о сложности в
определении, например, энергии гравитационных волн
на достаточно сложных фонах. На эту проблему в частной беседе
указал Копейкин [26].
.)
Тем не менее, с использованием фоновых и динамических
уравнений Эйнштейна равенство (4.52) подтверждается
прямыми расчетами. Такая ситуация говорит о сложности в
определении, например, энергии гравитационных волн
на достаточно сложных фонах. На эту проблему в частной беседе
указал Копейкин [26].
4.4.5 Разрешение неопределенности Боульвара-Дезера
Теперь рассмотрим последнюю:
четвертую проблему полевого подхода --
это неопределенность в выборе разбиений (4.31).
Если мы выберем произвольное из разбиений (4.31):
Разница лишь в том, что аргумент в этом уравнении зависит от выбора разбиения (4.53) и выражается через него как
Напомним, что суперпотенциал
Вернемся к методу Нетер-Белинфанте:
не было ограничений в выборе переменных, мы могли выбрать
любую из них:
![]() !
В результате, конечным и линейным оказался единственно КБЛ
суперпотенциал,
!
В результате, конечным и линейным оказался единственно КБЛ
суперпотенциал,
![]() , а затем новый суперпотенциал,
, а затем новый суперпотенциал,
![]() . Только для выбора
(4.31), или в
(4.55), единственно
. Только для выбора
(4.31), или в
(4.55), единственно
![]() суперпотенциал
суперпотенциал
![]() в (4.54) и
в (4.54) и
![]() совпадают.
Этот факт свидетельствует о преимуществе выбора (4.22).
Существуют и другие показания в пользу этого
выбора и разбиения, соответвующего ему.
Суперпотенциал Абботта-Дезера [22]
является одним из набора (4.54), а именно:
совпадают.
Этот факт свидетельствует о преимуществе выбора (4.22).
Существуют и другие показания в пользу этого
выбора и разбиения, соответвующего ему.
Суперпотенциал Абботта-Дезера [22]
является одним из набора (4.54), а именно:
![]() .
Однако мы [27] показали,
что такой суперпотенциал не дает правильного Бонди-Сакса импульса
на нулевой бесконечности, то есть не удовлетворяет одному из основных
естественных тестов,
в то время как
.
Однако мы [27] показали,
что такой суперпотенциал не дает правильного Бонди-Сакса импульса
на нулевой бесконечности, то есть не удовлетворяет одному из основных
естественных тестов,
в то время как
![]() дает нужный результат.
дает нужный результат.
<< 4.3 Проблемы полевой формулировки ОТО | Оглавление | Литература к Лекции 4 >>
![$\displaystyle \left[ {{\partial {\hat{\cal L}}_G} \over {\partial \left(\bar D_...
...
\overline D_\nu g_{\rho\sigma} - {\hat{\cal L}}_G \delta^\mu_\nu\right]\xi^\nu$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img516.gif)
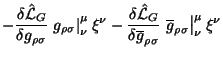
![$\displaystyle \left[{{\partial {\hat{\cal L}}^{(2)}} \over {\partial \left(\bar...
...erline D_\nu g_{\rho\sigma} - {\hat{\cal L}}^{(2)}\delta^\mu_\nu\right]
\xi^\nu$](http://images.astronet.ru/pubd/2001/09/12/0001170672/img527.gif)