Астронет > 4.3 Проблемы полевой формулировки ОТО

Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://variable-stars.ru/db/msg/1170672/node21.html

<< 4.2 Обобщенная полевая формулировка ОТО | Оглавление | 4.4 Метод Нетер-Белинфанте и ... >>

Разделы

4.3 Проблемы полевой формулировки ОТО

4.3.1 Дифференциальные законы сохранения для обобщенной формулировки

Для гравитационных уравнений (4.10) полевой формулировки $\hat G^L_{\mu\nu} + \hat \Phi^L_{\mu\nu} = \kappa{\hat t}^{(tot)}_{\mu\nu}$ дифференциальный закон сохранения (4.15) выполняется только для фонов, которые являются пространствами Эйнштейна по Петрову [18]. Таким образом, для Риччи-плоских фонов $\overline{R} = 0$ , в самом общем случае для пространств Эйнштейна $\overline {R_{\mu\nu}} = \Lambda \bar g_{\mu\nu}$ выполняется $\overline D_\nu \hat t^{(tot)\nu}_\mu = 0$ . Однако, для более общих фонов мы не имеем тождества типа (4.14), приходится констатировать, что $\overline D_\nu\left(\hat G^{L\nu}_{\mu} + \hat \Phi_{\mu}^{L\nu}\right) \neq 0$ и заключать, что $\overline D_\nu \hat t^{(tot)\nu}_\mu \neq 0$ . Этот факт мы [13] объяснили как следсвтие взаимодействия со сложным фоном, но только на качественном уровне. Таким образом, первую проблему мы формулируем так:

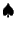$\spadesuit$ I? Можно ли построить дифференциальные законы сохранения на самом общем фоне? Как они выглядят, как выглядят члены взаимодействия с фоном?

4.3.2 Произвольные векторы смещений

Если фон -- это пространство Эйнштейна (то есть выполняется закон (4.14)) и фон имеет киллинговы векторы $\overline\xi^\alpha$ , тогда несложно построить сохраняющийся ток

$\partial_\nu \left(\hat t^{(tot)\nu}_\mu \overline\xi^\mu\right)= 0$ и соответствующие глобальные законы сохранения. Однако, как отмечалось в лекции 3 важными могут оказаться и не только киллинговы векторы. Ведь с помощью метода Нетер-Белинфанте оказалось возможным построить сохраняющиеся токи для произвольных векторов смещений. Поэтому вторую проблему мы сформулируем следующим образом:

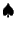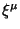$\spadesuit$ II? Можно ли построить сохраняющиеся токи для произвольных векторов $\xi^\mu$ и как они будут выглядеть
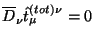(a) для случая $\overline D_\nu \hat t^{(tot)\nu}_\mu = 0$ ?

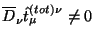(b) несмотря на то, что $\overline D_\nu \hat t^{(tot)\nu}_\mu \neq 0$ ?

4.3.3 Суперпотенциалы в полевой формулировке ОТО

Начиная с работ Толмена [19] и Фрейда [4.20] стало ясно, что суперпотенциалы в ОТО играют важную роль в построении законов сохранения. Есть также указания на то, что они имеют место и в обобщенной полевой формулировке ОТО. Давайте рассмотрим уравнения полевой формулировки на плоском фоне: $\hat G^{\mu\nu}_L = \kappa \hat t^{\mu\nu}_{(tot)}$ , где левая часть определенная в (4.11) может быть переписана в виде $\hat G^{\mu\nu}_L = \overline D_\rho \hat {\cal P}^{\mu\nu\rho}$ с суперпотенциалом Папапетроу [21]: $\hat {\cal P}^{\mu\nu\rho}$ . Таким образом, в этом простом случае обобщенный тензор энергии-импульса выражается через дивергенцию от суперпотенциала. Абботт и Дезер [22] построили обобщенный суперпотенциал Папапетроу для случая деситтеровского и анти-деситтеровского фона с векторами Киллинга этих же фонов. Третью проблему мы формулируем поэтому в виде:

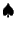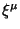$\spadesuit$ III? Каковы суперпотенциалы в самой общей форме и с произвольными $\xi^\mu$ в обобщенной полевой формулировке ОТО?

4.3.4 Неопределенность Боульвара-Дезера

Рассматривая различные разбиения для определения возмущений на плоском фоне типа $g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}$ , $\sqrt {-g}g^{\mu\nu} = \eta^{\mu\nu} + \hat l^{\mu\nu},...$ Боульвар и Дезер [23] установили, что тензоры энергии-импульса соответствующие этим разбиениям различаются, начиная со второго порядка по возмущениям. Мы [15] исследовали эту проблему в самом общем случае для произволных фонов. Для всех возможных разбиений типа

$\displaystyle g_{\mu\nu}$	=	$\displaystyle \bar g_{\mu\nu} + h_{\mu\nu},$
$\displaystyle \hat g^{\mu\nu}$	=	$\displaystyle \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}, \rightarrow g^A = \bar g^A + h^A$
$\displaystyle g^{\mu\nu}$	=	$\displaystyle \bar g^{\mu\nu} + r^{\mu\nu},$
....	=	............. ,	(4.31)

был построен свой вариант полевой формулировки с уравнениями

$\begin{displaymath} \hat G^{L(A)}_{\mu\nu} + \hat \Phi^{L(A)}_{\mu\nu} = \kappa{\hat t}^{(tot A)}_{\mu\nu}, \end{displaymath}$

(4.32)

где гравитационные возмущения взятые в форме $\hat l^{\mu\nu}_{(A)} \equiv h^A ({{ \partial \overline {\hat g^{\mu\nu}}} / {\partial \overline {g^A}}})$ обобщают $\hat l^{\mu\nu}$ . В общем случае была найдена неопределенность в тензоре энергии-импульса ${\hat t}^{(tot A)}_{\mu\nu}$ в уравнениях (4.32) для различных разбиений (4.31). Однако, до сих пор не ясно какое из разбиений (4.31) более предпочтительно. Четвертая проблема поэтому есть

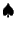$\spadesuit$ IV? Определение критерия для выбора наилучших h^A.

<< 4.2 Обобщенная полевая формулировка ОТО | Оглавление | 4.4 Метод Нетер-Белинфанте и ... >>