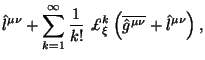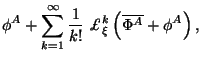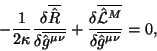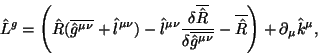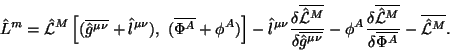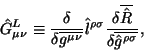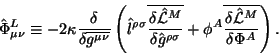Astronet Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://variable-stars.ru/db/msg/1170672/node20.html
<< 4.1 Фиксированные фоны в ОТО | Оглавление | 4.3 Проблемы полевой формулировки ОТО >>

Разделы

4.2 Обобщенная полевая формулировка ОТО

4.2.1 Обобщение модели Дезера

В работах [13]$^{\!- }$[16] мы обобщили подход предложенный Дезером [11]. Прежде всего, вместо пространства Минковского в лоренцевых координатах мы предлагаем использовать произвольно искривленный фон с заданной метрикой $\bar g_{\mu\nu}$ и заданными фоновыми материальными полями $\overline \Phi^A$, удовлетворяющими фоновым уравнениям Эйнштейна:

\begin{displaymath} \overline G_{\mu\nu} = \kappa \overline T_{\mu\nu}. \end{displaymath} (4.8)

Часто бывает полезным лишь Риччи-плоский фон: $\overline G_{\mu\nu} = 0$. Естественно, наша полевая формулировка с фоном (4.8) является ковариантной.

Как оказалось, использование формализма 1-го порядка вовсе не обязательно для построения полной и замкнутой (без бесконечных разложений) теории. Терия может быть построена так, что некоторые функции не будут иметь явного выражения через динамические переменные, но уравнения, которым они удовлетворяют достаточно просты и исследование не вызывает трудностей. Часто такой формализм 2-го порядка более удобен и здесь мы используем именно его для представления результатов.

Пока запишем действие, которое обобщает действие Дезера без конкретного вида лагранжианов (их мы определим позже) для гравитационного поля $\hat l^{\mu\nu}$ и набора материальных полей $\phi^A$:

\begin{displaymath} S = - {1 \over 2 \kappa c} \int{d^4x\hat L^g} + {1 \over c}\int{d^4x\hat L^m}. \end{displaymath} (4.9)

Мы полагаем, что поля $\phi^A$ являются произвольными тензорными плотностями. Варьирование (4.9) по гравитационным переменным $\hat l^{\mu\nu}$ дает уравнение
\begin{displaymath} \hat G^L_{\mu\nu}(l) + \hat \Phi^L_{\mu\nu}(l) = \kappa \lef... ...+ \hat t^{m}_{\mu\nu}\right) = \kappa \hat t^{(tot)}_{\mu\nu}, \end{displaymath} (4.10)

где ковариантизованный оператор безмассового поля спина 2, обобщающий оператор в (4.1), есть
\begin{displaymath} 2\hat G^L_{\mu\nu}(l) \equiv \overline D^\alpha_{ \alpha} \h... ...l^\alpha_{ \mu} - \overline D_{\alpha\mu}\hat l^\alpha_{ \nu}. \end{displaymath} (4.11)

Оператор $\hat \Phi^L_{\mu\nu}(l,\phi)$ определим позже, но заметим, что для Риччи-плоского фона $\overline R_{\mu\nu} = 0$ он исчезает и (4.10) преобразуется в
\begin{displaymath} \hat G^L_{\mu\nu}(l) = \kappa \left( \hat t^{gr}_{\mu\nu} + \hat t^{m}_{\mu\nu}\right) = \kappa \hat t^{(tot)}_{\mu\nu}. \end{displaymath} (4.12)

Правая часть в уравнениях (4.10) и (4.12) является симметричным (метричесмким) тензором энергии-импульса системы, соответствующим действию (4.9):
\begin{displaymath} \hat t^{gr}_{\mu\nu} = -{1\over{\kappa}} {{\delta{\hat L^g}}... ..._{\mu\nu} = 2{{\delta{\hat L^m}}\over{\delta\bar g^{\mu\nu}}}. \end{displaymath} (4.13)

Оказывается, что для Риччи-плоского фона дивергенция от левой части уравнений (4.12) обращается тождественно в нуль:
\begin{displaymath} \overline D_\nu \hat G^{L\nu}_{\mu}(l) \equiv 0, \end{displaymath} (4.14)

а это ведет к закону сохранения
\begin{displaymath} \overline D_\nu \hat t^{(tot)\nu}_{\mu} = 0. \end{displaymath} (4.15)

Такой закон не выполняется для общего фона в уравнениях (4.10) и эта проблема будет обсуждаться позже.

Аналогично тому как построены гравитационные уравнения (4.10) строятся материальные уравнения, где левая часть линейна по динамическим переменным, а правая представляет некоторый ,,ток''.

Эквивалентность ОТО устанавливается после отождествлений

\begin{displaymath} \sqrt{-g}g^{\mu\nu} \equiv \hat g^{\mu\nu} \equiv \overline ... ...\nu}} +\hat l^{\mu\nu},    \Phi^A = \overline \Phi^A + \phi^A, \end{displaymath} (4.16)

которые обобщают (4.5) или (4.7).

В сравнении с работой Дезера нами [13]$^{\!- }$[16] была подробно ,,обозначена'' и исследована калибровочная (так называемая внутренняя) инвариантность. То есть инвариантность относительно преобразований, которые не затрагивают ни координат, ни фоновой метрики с фоновыми полями. Эти преобразования выглядят так


$\displaystyle {\hat l}'^{\mu\nu}$ = $\displaystyle \hat l^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}}  \hbox{$\pounds$}_\xi^k \left(\overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}\right),$  
$\displaystyle {\phi}'^A$ = $\displaystyle \phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline{\Phi^A}+\phi^A\right),$ (4.17)

где, вообще говоря, не предполагается ни малости полей, ни малости калибровочных функции (конечно, без предположений о малости необходимо учитывать все порядки в бесконечных рядах). Инвариантность состоит в следующем. Лагранжиан в (4.1) инвариантен для преобразований (4.17) с точностью до дивергенции на фоновых уравнениях движения. Таким образом, само действие (4.1) инвариантно с точностью до поверхностных членов. Уравнения движения являются калибровочно инвариантными на них самих (то есть, если они удовлетворены) и на фоновых уравнениях. Тензор энергии-импульса калибровчно инвариантен, но с точностью до дивергенции:
\begin{displaymath} {\hat t}'^{(tot)}_{\mu\nu} = {\hat t}^{(tot)}_{\mu\nu} + {1 \over \kappa} \hat G^L_{\mu\nu}\left(l' - l\right), \end{displaymath} (4.18)

где оператор $\hat G^L_{\mu\nu}\left(l' - l\right)$ определен в (4.11) и является 4-ковариантной дивергенцией. Подробнее свойства и некоторые приложения калибровочных преобразований в полевом подходе будут даны в следующей лекции 5.

4.2.2 Принципы построения обощенной полевой формулировки ОТО

Развивая полевую формулировку ОТО (см. уравнения (4.8) - (4.18)), для построения мы [13] использовали принцип предложенный Дезером:

Таким образом строятся уравнения (4.12). В более сложном случае уравнений (4.10) принцип построения источника в правой части сохраняется, усложняется лишь определение левой линейной части.

Другой принцип, используется в работе Грищука [17] и может быть сформулирован как

Способ построения по этому принципу заключается в обобщении закона Нютона $\Delta \phi = 4\pi G\rho$ на случай специальной теории относительности:


(i) Сначала одна компонента плотности $\rho$ заменяется на 10 компонент материального тензора энергии-импульса $T_{\mu\nu}$.

(ii) Из этого следует, что одну компоненту гравитационного потенциала $\phi$ нужно заменить 10-ю гравитационными потенциалами $h^{\mu\nu}$.

(iii) Далее необходимо лапласиан $\Delta $ заменить на даламбертиан, как это должно быть в специальной теории относительности: $h_{\mu\nu ,\alpha}^{   ,\alpha} = \kappa T_{\mu\nu}$.

(iv) Следующий шаг -- это включение самодействия:

$h_{\mu\nu ,\alpha}^{   ,\alpha} = \kappa\left(T_{\mu\nu} + t^{gr}_{\mu\nu}\right) = \kappa t^{(tot)}_{\mu\nu}$.

(v) И, наконец, добавление к левой части членов

$\eta_{\mu\nu}h^{\alpha\beta}_{   ,\alpha\beta}- h^{\alpha}_{  \mu,\nu\alpha} - h^{\alpha}_{  \nu,\mu\alpha}$ востанавливает калибровочную инвариантность теории.


В результате получаются уравнения $G^L_{\mu\nu}(h) = \kappa t^{(tot)}_{\mu\nu}$, которые есть уравнения (4.12) и есть точно уравнения Эйнштейна.

Третий принцип основывается на калибровочно инвариантных свойствах полевой формулировки [16] и близок к тому как могут быть построены многие из калибровочных теорий. Этот принцип построения заключается в локализации параметров некоторой группы преобразований, относительно которой исходная теория инвариантна. Локализация заключается в том, что постоянные параметры становятся зависимыми, скажем, от координат. Возникшая неинвариантность компенсируется как раз вновь введенными каллибровочными (компенсирующими) полями. Наш принцип звучит как

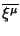и сводится к следующему:

(i) Рассмотрим систему динамических полей $\phi^A$ на заданном фоне (с метрикой $\bar g^{\mu\nu}$ и обладающим векторами Киллинга $\overline {\xi^\mu}$) с лагранжианом $L^M(\phi^A, \bar g^{\mu\nu})$.

(ii) Относительно ,,калибровочных'' преобразований $\phi'^A \rightarrow \phi^A + \hbox{$\pounds$}_{\bar\xi}\phi^A$, в линейном приближении по $\overline {\xi^\mu}$, уравнения системы инвариантны на самих себе, а лагранжиан инвариантен с точностью до дивергенции.

(iii) Теперь ,,локализуем'' какой либо из векторов $\overline {\xi^\mu}$, здесь под локализацией мы понимаем замену вектора Киллинга на произвольный вектор $\xi^\mu$.

(iv) После этого требуем сохранения прежней инвариантности. Чтобы удовлетворить этому требованию необходимо ввести компенсирующее (гравитационное) поле $h^{\mu\nu}$ таким образом, что $\bar g^{\mu\nu} \rightarrow \bar g^{\mu\nu} + h^{\mu\nu}$. Последовательное построение теории полей $h^{\mu\nu}$ приводит к обобщенной полевой формулировке ОТО.

4.2.3 Построение обощенной полевой формулировки ОТО с помощью разделения на фон и динамические поля

Четвертый принцип построения обощенной полевой формулировки мы выделяем в отдельный подпункт, поскольку уделим ему больше внимания. Именно такое построение дает более наглядную связь между полевой формулировкой и обычной геометрической формулировкой ОТО. Действительно, если это есть всего лишь различные представления одной и той же теории и переход от полей формулировки к геометрической достигается с помощью отождествлений (4.16), то вероятно, что переход от геометрической формулировки к полевой мог бы осуществляться с помощью разбиения типа (4.16). Действительно, часто по тем или иным причинам в ОТО делают разбиение эйнштейновской метрики на фоновую и динамическую части:

\begin{displaymath} g_{\mu\nu} = \bar g_{\mu\nu} + h_{\mu\nu}. \end{displaymath} (4.19)

Затем, подставляют (4.19) в уравнения Эйнштейна, оставляют в левой части лишь линейные по возмущениям члены, а все остальное переносят вправо и называют этот источник ,,эффективным'' тензором энергии-импульса:
\begin{displaymath} G^L_{\mu\nu}(h) = \kappa t^{(eff)}_{\mu\nu}. \end{displaymath} (4.20)

В таком подходе нет ничего противоречивого. Однако само построение является эвристическим и многие его свойства не так уж просто выяснить. Мы [15] развили подход (4.19) - (4.20) как полевую теорию со всеми ее атрибутами. То есть представлен лагранжиан, из которого следуют уравнения и тензор энергии-импульса, следуют калибровочные свойства. Здесь мы представляем основные элементы этого подхода. Сначала сформулируем сам принцип построения:

Рассмотрим обычное дествие ОТО:

\begin{displaymath} S = {1 \over c} \int d^4x {\hat{\cal L}}^{GR} \equiv -{1 \... ...+ {1 \over c} \int d^4x {\hat{\cal L}}^M (\Phi^A, g_{\mu\nu}). \end{displaymath} (4.21)

Сделаем разложение переменных на фоновые и динамические части,
\begin{displaymath} \hat g^{\mu\nu} \equiv \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu},    \Phi^A \equiv \overline {\Phi^A} + \phi^A \end{displaymath} (4.22)

где фоновые переменные являются решениями фоновых уравнений Эйнштейна:
\begin{displaymath} -{1 \over {2\kappa }} {{\delta \overline{\hat R}} \over {\d... ...t{\cal L}}^M}} \over {\delta \overline{\hat g^{\mu\nu}}}} = 0, \end{displaymath} (4.23)


\begin{displaymath} {{\delta \overline{{\hat{\cal L}}^M}} \over {\delta \overline{\Phi^A}}} = 0. \end{displaymath} (4.24)

Разбиения (4.22) точно обратны отождествлениям (4.16) и обобщают (4.19), а уравнения (4.23) -- это уравнения (4.8). Построение динамического лагранжиана [15]:
\begin{displaymath} {\hat{\cal L}}^{dyn} = {\hat{\cal L}}^{GR} - {\hat{\cal L}}^{(1)} - {\hat{\cal L}}^{(0)} + div, \end{displaymath} (4.25)

-- это есть обощение конструкции Дезера [11]. Лагранжиан (4.25) -- это лагранжиан в действии (4.9):
   
  $\displaystyle {\hat{\cal L}}^{dyn} = -{1\over{2\kappa}}\hat L^g + \hat L^m,$  

где ${\hat{\cal L}}^{(0)} \equiv \overline{{\hat{\cal L}}^{GR}} $, ${\hat{\cal L}}^{(1)}$ пропорционален уравнениям (4.23) и (4.24), а $div = \partial_\mu \hat k^\mu $ c $\hat k^\mu \equiv \hat g^{\mu\rho} \Delta^\sigma_{\rho\sigma} - \hat g^{\rho\sigma} \Delta^\mu_{\rho\sigma}$ и $\Delta^\mu_{\rho\sigma} = \Gamma^\mu_{\rho\sigma}- \overline{ \Gamma^\mu_{\rho\sigma}}$, такая же как в КБЛ модели. Конкретно гравитационная и материальные части имеют следующее явное выражение:
\begin{displaymath} \hat L^g = \left(\hat R (\overline {\hat g^{\mu\nu}} + \hat ... ...\nu}}}} - \overline{\hat R}\right) + \partial_\mu \hat k^\mu, \end{displaymath} (4.26)


\begin{displaymath} \hat L^m = {\hat{\cal L}}^M\left[(\overline {\hat g^{\mu\nu... ...over{\delta \overline{\Phi^A}}} - \overline{{\hat{\cal L}}^M}. \end{displaymath} (4.27)

Варьирование действия (4.9) со значениями лагранжианов (4.26) и (4.27) по гравитационным переменным дает уравнение (4.10):

   
  $\displaystyle \hat G^L_{\mu\nu} + \hat \Phi^L_{\mu\nu} = \kappa\left({\hat t}^g_{\mu\nu} + {\hat t}^m_{\mu\nu}\right) \equiv \kappa{\hat t}^{(tot)}_{\mu\nu},$  

где гравитационная линейная часть (4.11) может быть записана как
\begin{displaymath} \hat G^L_{\mu\nu} \equiv {\delta \over {\delta\overline{g^{... ...verline{\hat R}}\over{\delta \overline{\hat g^{\rho\sigma}}}}, \end{displaymath} (4.28)

а линейная материальная часть как
\begin{displaymath} \hat \Phi^L_{\mu\nu} \equiv -2\kappa {\delta \over {\delta\o... ...ine{{\delta {{\hat{\cal L}}^M}}\over{\delta {\Phi^A}}}\right). \end{displaymath} (4.29)

Полный тензор энергии-импульса соответствующий (4.9) и по частям представленый в (4.13) есть
\begin{displaymath} {\hat t}^{(tot)}_{\mu\nu} \equiv 2{{\delta{\hat{\cal L}}^{dy... ...^{\mu\nu}}}} \equiv {\hat t}^g_{\mu\nu} + {\hat t}^m_{\mu\nu}. \end{displaymath} (4.30)

В следующей лекции 5, используя общековариантные свойства системы (4.21) и разбиения (4.22), мы покажем как получить все калибровочные свойства полевой формулировки.


<< 4.1 Фиксированные фоны в ОТО | Оглавление | 4.3 Проблемы полевой формулировки ОТО >>

Rambler's Top100 Яндекс цитирования