Астронет > 3.4 Использование и интерпретация новых интегральных соотношений

Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://variable-stars.ru/db/msg/1170672/node16.html

<< 3.3 Законы сохранения и ... | Оглавление | Литература к Лекции 3 >>

Разделы

3.4 Использование и интерпретация новых интегральных соотношений

3.4.1 Связевые интегральные векторы Трашен и эффект Сакса-Вольфа

На качественном уровне мы представляем результат [2], где показано, что если на возмущения материальной составляющей на космологическом фоне наложены ограничения, то есть они удовлетворяют так называемым интегральным связям, эффект Сакса-Вольфа может быть ослаблен. Для этого нужно представлять, что такое локализованные возмущения. Сначала определим их в плоском пространстве-времени. Пусть в начальный момент времени t = 0 плотность $\rho$ является однородной. В следующий момент t > 0 в объеме V возникают возмущения $\delta\rho$ , которых нет на границе объема $\partial\Sigma$ . Эти возмущения называются локализованными, если они удовлетворяют интегральным соотношениям

$\begin{displaymath} \int_\Sigma \delta\rho dV =0, \int_\Sigma \vec x \delta\rho dV =0, \end{displaymath}$

(3.30)

которые называются интегральными связями.

В ОТО интегральные связи имеют вид:

$\begin{displaymath} \int_\Sigma \delta T^\alpha_\mu V^\mu n_\alpha dV = \oint_{\partial\Sigma} B^l d S_l. \end{displaymath}$

(3.31)

Их смысл в том, что задавая граничные условия мы ограничиваем возмущения внутри объема. Аналогично (3.30), локализованные возмущения в ОТО определяются как

$\begin{displaymath} \int_\Sigma \delta T^\alpha_\mu V^\mu n_\alpha dV = 0. \end{displaymath}$

(3.32)

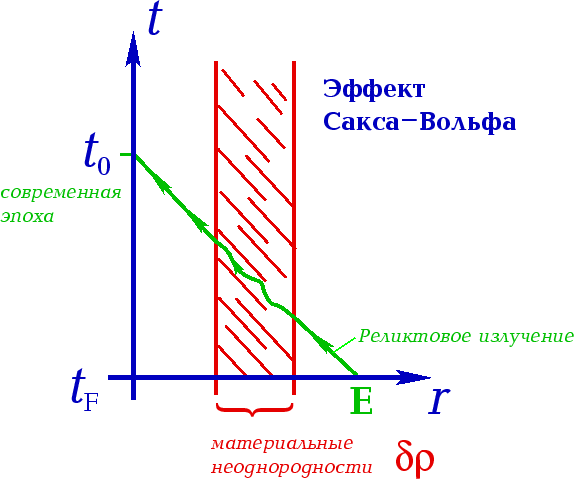
Для фридмановской модели существует 10 таких векторов $V^\alpha$ , 6 из них -- это уже известные киллинговы векторы фридмановского фона. Оставшиеся 4 вектора -- это как раз векторы Трашен [1].

Рис.2.

Эффект Сакса-Вольфа [3] заключается в том, что неоднородности $\delta\rho$ на пути фонового космологического излучения (Рис. 2) вносят вклад в анизотропию фоновой температуры. Существование интегральных связевых векторов Трашен ведет к существованию локализованных возмущений типа (3.32), которые ослабляют этот эффект [2].

Теперь обратимся к объемным интегралам в (3.27) - (3.29). Кроме $\delta T^0_\mu$ подинтегральные выражения в объемных интегралах содержат лишь ${\cal Q}$ и ${\tilde h}^m_m$ . Существуют 4 линейных комбинации F, которые не включают ${\tilde h}^m_m$ ; они связаны со следующими линейными комбинациями конформных киллинговых векторов:

$\begin{displaymath} {\bf V}_0\equiv \left.(\dot a^{-1}{\bf a}^{\dag }-{\bf d}^{\... ...bf V}_a\equiv\dot a^{-1}{\bf l}^{\dag }_a+ k{\bf b}^{\dag }_a. \end{displaymath}$

(3.33)

Вектора ${\bf V}_0$ and ${\bf V}_a$ оказываются как раз векторами Трашен, а в калибровке ${\cal Q}=0$ соответствующие интегральные соотношения с F обращаются в интегральные связи Трашен.

3.4.2 Калибровочные условия и интегральные соотношения

В соотношениях (3.27) - (3.29) не были фиксированы калибровочные условия, то есть свобода выбора в отображении возмущенного пространства-времени на фоновое не была использована. Одно из условий, которое упрощает почти все подинтегральные выражения есть так называемая калибровка ,,однородного хаббловского расширения'' ${\cal Q}=0$ активно обсуждаемая Бардином [13]. При этом 14 из 15 объемных подинтегральных выражений редуцируются в комбинации только $\delta T^0_\mu$ . Таким образом, эти 14 соотношений вполне приобретают форму (3.31) и представляют новый набор интегральных связей. Объемные интегралы в этих интегральных связях представляют моменты материального тензора энергии-импульса порядков 0, 1 и 2 по x^a, когда k=0, и близкую интерпретацию когда $k=\pm 1$ . Оставшийся интеграл содержит как $\delta T^0_\mu$ , так и ${\tilde h}^m_m$ : для $k=\pm 1$ он относится к конформным временным трансляциям $F({\bf t})$ , а для k=0 к временным ускорениям $F({\bf a}^{\dag })$ .

Часто используется другое калибровочное условие $\nabla_l \vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}=0$ (см., например, работу [14]), в котором $\vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}$ -- бесследовая часть ${\tilde h}^l_k$ . Комбинируя $\nabla_l \vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}=0$ с ${\cal Q}=0$ (эти 4 условия использовались Бичаком в неопубликованной работе) мы находим, что существуют 4 соотношения, которые не зависят от гравитацинного излучения:


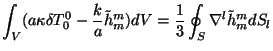		$\displaystyle \int_V (a\kappa \delta T^0_0-{k\over a}{\tilde h}^m_m)dV= {1\over 3}\oint_S \nabla^l{\tilde h}^m_m dS_l$


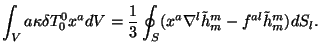		$\displaystyle \int_V a\kappa\delta T^0_0x^adV= {1\over 3}\oint_S (x^a\nabla^l{\tilde h}^m_m-f^{al}{\tilde h}^m_m) dS_l.$

Таким образом, в этой калибровке интегралы энергии $\int \delta T^0_0$ и центра масс

$\int\delta T^0_0x^a/\int \delta T^0_0$ определяются лишь следом ${\tilde h}^m_m$ .

<< 3.3 Законы сохранения и ... | Оглавление | Литература к Лекции 3 >>