 |
Астронет: В. А. Батурин, И. В. Миронова Звезды: их строение, жизнь и смерть http://variable-stars.ru/db/msg/1170638/structure/equation/hydrostat/vec_equat.htm |
| предыдущая |
следующая
|
Векторное уравнение второго порядка в самосопряженном виде
В некоторых случаях уравнение гидростатического равновесия вместе с уравнением
для гравитационного потенциала можно привести к векторному уравнению второго
порядка для одной неизвестной. Естественно, что это возможно приналичии некоторой
дополнительной информации (уравнения), позволяющей исключить одну из неизвестных
величин. Например, положим, давление есть известная функция плотности P(
)
. Это, конечно не верно в общем случае, однако даже когда это не так, полученное
нами уравнение может быть полезно в локальном анализе - в окрестности любой
точки модели можно аппроксимировать поведение давления некоторой функцией только
плотности.
Возвращаясь к нашим уравнения, заметим, что удобной формой могло быть уравнение Пуассона - с неизвестной в виде потенциала и стандартным видом дифференциального оператора Лапласа. В этом случае нам осталось найти подходящее выражение плотности через потенциал, например в виде
(то есть мы ищем функцию f, такую что 
=f()).
Для ее нахождения нужно вспомнить о уравнении гидростатического равновесия,
в векторной форме. По нашим предположениям,
давление есть функция плотности, поэтому слева есть некоторая функция плотности.
Если бы удалось эту функцию плотности выразить как градиент некоторой другой
функции плотности, то после интегрирования мы получили бы интересующую нас замену.
Другими словами, нужно решить уравнение вида
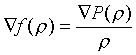
относительно неизвестной функции f, считая независимой
переменной . Формальное решение очевидно имеет вид
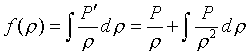
(второе равенство есть просто интегрирование по частям). Таким образом, используя полученную нами функцию f, можно записать векторное уравнение второго порядка для потенциала в виде
Данное уравнение справедливо в пространстве любой размерности, и в координатах с любой симметрией (сферические, цилиндрические и т.д.)
Пример применения для политропных конфигураций
Исторически наиболее известным случаем использования упрощенных предположений
при построении моделей звезд является случай политропных звезд, то есть случай
P=K
. Тогда искомая функция, связывающая
потенциал и плотность, имеет вид
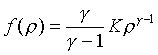
а общее уравнение для политропной конфигурации имеет вид (с использованием масштабируемого радиуса для приведения к безразмерному виду)
или с учетом сферической симметрии, в виде уравнения второго порядка
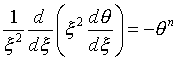
(здесь 
и 
- безразмерные потенциал и радиус).
В случае изотермической конфигурации, когда P=K,
уравнение переходит в
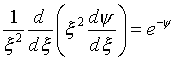
Отметим, что изотермические конфигурации имеют бесконечную протяженность, и неограниченную потенциальную энергию. Поэтому последнее уравнение может иметь смысл только как локальное.
В.Батурин
| предыдущая |
следующая
|