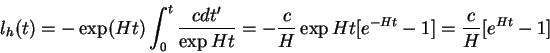 |
Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков http://variable-stars.ru/db/msg/1170612/node63.html |
<< 12. Космология (продолжение II) | Оглавление | 12.2 Инфляционная Вселенная >>
12.1 Трудности классической космологии
Стройная теория фридмановской космологии (метрика
Робертсона-Уокера, нестационарные решения уравнений Эйнштейна)
модель горячей Вселенной (первичный нуклеосинтез,
объяснение реликтового излучения), подтвержденная
обширными астрономическими наблюдениями, довольно
быстро столкнулась с рядом трудностей. Коротко говоря,
они сводятся к тому, что масштабный фактор Вселенной 
увеличивается слишком медленно со временем (как 
или 
в плоской модели),
поэтому в прошлом малым временам 
должны соответствовать
слишком большие масштабные факторы 
. Парадоксы классической космологии
решаются в модели инфляционной Вселенной, в которой предполагается,
что на самых ранних стадиях эволюции
масштабный фактор рос экспоненциально:
const.
12.1.1 Проблема горизонта (проблема причинности)
Реликтовое излучение наблюдается изотропно со всех направлений на небе.
После момента рекомбинации (
,
с)
оно практически не взаимодействует с веществом в расширяющейся Вселенной.
Физический размер горизонта на момент рекомбинации порядка
, поэтому участки неба с угловыми размерами
(фактор красного смещения появился из отншения
масштабных факторов в момент 
и 
) оказываются
причинно-несвязанными между собой. Отчего же мы наблюдаем столь изотропное
распределение вещества и реликтового излучения? Так как во Фридмановских
моделях горизонт растет
пропорционально времени, прошедшего с момента начала расширения,
в будущем, конечно, любые области "войдут под
горизонт".
Переформулировать проблему горизонта можно в терминах энтропии Вселенной.
Современная энтропия сосредоточена в релятивистских частицах
(фотонах, нейтрино). Безразмерная энтропия (т.е. в единицах
постоянной Больцмана 
) в единице объема
для релятивистских частиц (независимо, бозоны
это или фермионы) есть
(cм. напр. Зельдович и Новиков, Релятивистская Астрофизика, М., Наука,
1967, раздел 8.5). Плотность релятивистских частиц (фотонов + нейтрино )
в современную эпоху
см
,
а значит энтропия Вселенной внутри сегодняшнего горизонта
, то внутри горизонта
на радиационно-доминированной стадии
Постоянная Хаббла на стадии доминирования релятивистской плазмы с плотностью энергии
определяется из
соотношения
где
г
ГэВ -
Планковская масса. Т.о. внутри горизонта в планковскую эпоху
Значит, столь "горячая" теперь Вселенная на самых ранних стадиях должна была бы состоять из
независимых,
причинно-несвязанных
областей! Отчего же тогда наблюдаемая картина так однородна
и изотропна?
Если же была эпоха, когда масштабный фактор рос экспоненциально,
любые изначально причинно-связанные области быстро "расходились"
на расстояния 
горизонта (
). Значит, нет ничего
удивительного в том, что эти области на стадии более
медленного роста масштабного фактора видны как причинно-несвязанные.
Действительно, для закона (12.1) физический размер горизонта
, т.е. они находились в причинно-связанной области,
то
быстро выходит за горизонт
(т.е. становится больше 
), однако при этом
частицы как бы "помнят" о своей связи в прошлом.
Кинематику экспоненциального расширения можно также пояснить в терминах
поведения сопутствующей координаты горизонта
. По своему физическому смыслу сопутствующая
координата частицы является ее лагранжевой координатой и не
изменяется в ходе расширения. Именно в этих коодинатах изучается
процесс роста начальных возмущений, приведших в дальнейшем к
формированию структуры Вселенной.
На стадии инфляции сопутствующая координата горизонта
остается почти постоянной:
Отсюда следует, что при экспоненциальном расширении даже в бесконечно удаленном будущем световыми сигналами смогут обменяться только те точки, которые первоначально находились внутри сферы радиуса
.
Напротив, на Фридмановской стадии
,
, сопутствующая координата горизонта
является растущей функцией времени
и при фридмановском расширении в причинно-связанной области
в будущем окажется все пространство.
Для "рождения" Вселенной с
радиус причинно-связанной сферы
cм,
однако за 70 Хаббловских времен при экспоненциальном расширении
за время этой стадии 
он вырастет до
см, что достаточно для решения
проблемы горизонта. В современных моделях инфляции 
,
так что размер причинно-связанной области в прошлом намного превышает размер
современного горизонта.
12.1.2 Проблема плоского мира
Эта проблема состоит в чрезвычайной близости плотности к критической (т.е.
) на самых ранних стадиях эволюции. Вот простое рассуждение.
Предположим, что квантовое "рождение" мира произошло в момент
с. Естественный радиус кривизны мира при рождении
-
см. Для оценки предположим, что расширение Вселенной
все время происходило по степенному закону
. К настоящему
моменту 
лет радиус кривизны должен был бы вырасти
до размеров ...
см !
Проделаем обратные оценки: в настоящее время радиус кривизны
см, идя в прошлое к моменту 
получаем радиус кривизны
см,
а размер горизонта порядка
. Последнее неравенство
означает, что в эту эпоху
Вселенная оказывается плоской c точностью до
,
или в терминах
- с точностью до 
!!!
Как объяснить столь точную "настройку"?
К тем же выводам можно придти при более точном количественном рассмотрении.
Действительно, уравнение Фридмана для масштабного фактора
12.1можно переписать
через
и постоянную Хаббла 
в виде
для плоской модели или 
(закрытая или открытая модель).
Заметим, что правая часть представляет собой квадрат отношения Хаббловской
длины 
12.2
к радиусу кривизны 
12.3.
На Фридмановской стадии
, и
при 
, т.е. Хаббловский радиус
растет быстрее радиуса кривизны (масштабного фактора) и
величина 
всегда уменьшается. Поэтому факт близости
наблюдаемой Вселенной к плоской (
) очень странен.
12.4
Потребуем уменьшения правой части (12.4)
в ходе расширения, так чтобы независимо от начальной кривизны
Вселенная автоматически стремилась к плоской при расширении. Это условие
эквивалентно уменьшению сопутствующей Хаббловской координаты со временем
. Отсюда получаем эквивалентное требование на
масштабный фактор 
. Это условие выполняется при
экспоненциальном расширении
.
<< 12. Космология (продолжение II) | Оглавление | 12.2 Инфляционная Вселенная >>