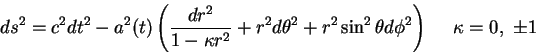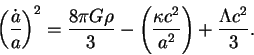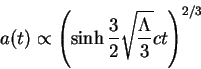|
Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков http://www.astronet.ru/db/msg/1170612/10lec/node3.html |
<< 10.1 Фридмановская космология | Оглавление | Литература >>
10.2 Модели Фридмана с космологической постоянной
Как отмечалось выше, современные данные убедительно
свидетельствуют в пользу наличия значительной доли полной
энергии Вселенной в форме космологической постоянной
(с эффективным уравнением состояния ![]() ) или
гипотетической квинтэссенции с
) или
гипотетической квинтэссенции с
![]() .
Поэтому ниже для справок мы приводим основные формулы
модели однородной изотропной Всленной (модель Фридмана-
Робертсона-Уокера) с космологической постоянной.
.
Поэтому ниже для справок мы приводим основные формулы
модели однородной изотропной Всленной (модель Фридмана-
Робертсона-Уокера) с космологической постоянной.
Однородная и изотропная Вселенная может быть описана нестационарной
(т.е. зависящей от времени) метрикой специального вида
(т.н. метрика Фридмана-Робертсона-Уокера)
Замечание. Из вида интервала
![]() , где
, где
![]() - элемет координатного расстояния, автоматически
получается закон Хаббла. Действительно, как следует из
записи для интервала, физическое расстояние есть
- элемет координатного расстояния, автоматически
получается закон Хаббла. Действительно, как следует из
записи для интервала, физическое расстояние есть
![]() ,
т.е.
,
т.е. ![]() . Пусть координаты точек не меняются,
. Пусть координаты точек не меняются,
![]() . Скорость изменения физического
расстояния тем не менее не равна нулю
. Скорость изменения физического
расстояния тем не менее не равна нулю
![]() . Интегрируя
вдоль геодезической (т.е. вдоль луча распространения света),
получается закон Хаббла:
. Интегрируя
вдоль геодезической (т.е. вдоль луча распространения света),
получается закон Хаббла: ![]() , где
, где
![]() - "постоянная"
Хаббла.
- "постоянная"
Хаббла.
Подставляя этот интервал в уравнения ОТО Эйнштейна,
получаем уравнения Фридмана для эволюции масштабного
фактора. Приведем их без вывода сразу для ненулевой
космологической постоянной ![]() (которая, вообще говоря, может
быть функцией времени).
Уравнение энергии:
(которая, вообще говоря, может
быть функцией времени).
Уравнение энергии:
Уравнение движения:
Уравнение неразрывности:
Замечания
1. В этих уравнениях нет произвольных констант, т.е.
при заданной топологии (
![]() ) и
) и ![]() эволюция происходит по определенному закону, зависящему
от связи давления и плотности
эволюция происходит по определенному закону, зависящему
от связи давления и плотности ![]() (уравнение состояния).
(уравнение состояния).
2. Обозначим ![]() - параметр Хаббла, и поделим
на
- параметр Хаббла, и поделим
на ![]() обе части уравнения энергии (10.11).
Вводя безразмерные переменные
обе части уравнения энергии (10.11).
Вводя безразмерные переменные
![]() ,
,
![]() ,
,
![]() записываем уравнение
энергии в компактном виде
записываем уравнение
энергии в компактном виде
3. Космологическая постоянная ![]() имеет размерность
имеет размерность
![]() см
см![]() . В безразмерной записи
современные наблюдения указывают на
значение
. В безразмерной записи
современные наблюдения указывают на
значение
![]() , откуда следует, что
в современную эпоху "плотность энергии вакуума" (именно физический вакуум
может играть роль положительной космологической постоянной
с
, откуда следует, что
в современную эпоху "плотность энергии вакуума" (именно физический вакуум
может играть роль положительной космологической постоянной
с ![]() )
)
Плотность энергии вакуума не изменяется при адиабатическом расширении
4. Уравнение (10.12) можно переписать в виде уравнения
движения точки на поверхности сферы радиуса ![]() (см. предыдущее
рассмотрение) с массой
(см. предыдущее
рассмотрение) с массой ![]() :
:
5. Знак пространственной кривизны (т.е. гауссовой кривизны
3-мерной гиперповерхности постоянного времени) не изменяется
в ходе эволюции Вселенной, хотя величина ее, разумеется,
зависит от времени.
Подчеркнем, что топология определяется полной плотностью
энергии, которая включает в себя
плотность всех видов материи (видимой (барионной) и невидимой
(небарионной)), имеющих положительное давление и являющихся
источником гравитации,
и плотность
"невидимой энергии" (англ. "dark energy" -
космологической постоянной или квинтэссенции)
с отрицательным давлением, создающих антигравитацию
в больших масштабах:
![]() .
Современные наблюдения (см. выше) дают
.
Современные наблюдения (см. выше) дают
![]() , т.е. возможный
радиус кривизны больше нескольких Хаббловских радиусов
, т.е. возможный
радиус кривизны больше нескольких Хаббловских радиусов
![]() см.
см.
6. В интересующем нас случае
![]() для пылевидной материи
(без давления,
для пылевидной материи
(без давления, ![]() )
есть аналитическое решение для роста масштабного фактора
)
есть аналитическое решение для роста масштабного фактора
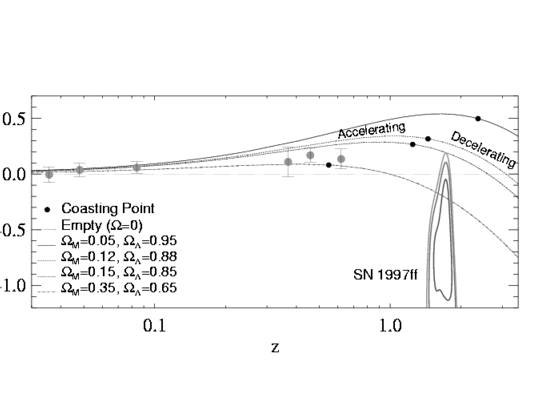 |
| Рис. 10.6
Разница в модулях расстояния известных
космологических сверхновых Ia в различных космологических моделях относительно
модели линейно однородно расширяющейся Вселенной
("пустая Вселенная" с |
<< 10.1 Фридмановская космология | Оглавление | Литература >>