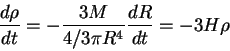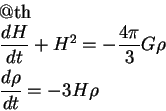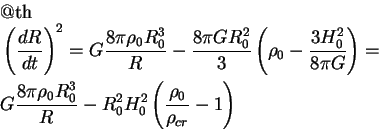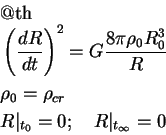|
Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков http://www.astronet.ru/db/msg/1170612/10lec/node2.html |
<< 10. Космология | Оглавление | 10.2 Модели Фридмана с >>
- 10.1.1 Космологический принцип
- 10.1.2 "Краткий курс" истории космологии ХХ века
- 10.1.3 Закон Хаббла
- 10.1.4 Закон эволюции. Критическая плотность
- 10.1.5 Влияние давления
10.1 Фридмановская космология
В этом разделе рассмотрим однородные и изотропные космологические модели Вседенной, впервые рассмотренные А.А. Фридманом в 1922 г. и носящие его имя.
10.1.1 Космологический принцип
Подобно принципу потоянства скорости света или принципу эквивалентности (которые лежат в основе общей теории относительности), в основе современных космологических моделей лежит космологический принцип, согласно которому во Вселенной не должно быть выделенных наблюдателей. Иногда этот принцип называют "принципом Коперника", который первый в новой истории отказался от геоцентрической системы мира. Этот принцип означает, что глобальные характеристики Вселенной одинаковы для любого наблюдателя, находящегося в любой точке гиперповерхности постоянного времени.
В настоящее время этот принцип с огромной точностью
подтвержден астрономическими наблюдениями
однородности распределения материи во Вселенной
в больших масштабах
(![]() Мпк) и изотропии (отсутствие выделенного
направления на уровне флюктуаций температуры реликтового фона
Мпк) и изотропии (отсутствие выделенного
направления на уровне флюктуаций температуры реликтового фона
![]() ). Уже одного этого оказывается достаточным,
чтобы из всего мыслимого многообразия возможных математических моделей,
описывающих Вселенную в целом, выбрать весьма узкий класс однородных
изотропных пространств (т.н.
модели Фридмана-Робертсона-Уокера). См. подробнее в непревзойденной
монографии С.Вейнберга
"Гравитация и космология", М.: Мир, 1975, Гл. 13 и далее).
). Уже одного этого оказывается достаточным,
чтобы из всего мыслимого многообразия возможных математических моделей,
описывающих Вселенную в целом, выбрать весьма узкий класс однородных
изотропных пространств (т.н.
модели Фридмана-Робертсона-Уокера). См. подробнее в непревзойденной
монографии С.Вейнберга
"Гравитация и космология", М.: Мир, 1975, Гл. 13 и далее).
10.1.2 "Краткий курс" истории космологии ХХ века
Очень схематично новейшую историю современной
космологии можно проследить по датам важнейших наблюдательных
и теоретических открытий:
1910-1922, В. Слайфер, красные смещения в спектрах галактик
где
1916, А. Эйнштейн, Общая теория относительности
1922-24, А. Фридман, нестационарные решения уравнений
Эйнштейна (фридмановские космологические модели)
1929, Э. Хаббл, закон ![]() для удаляющихся галактик.
Скорость удаления галактики определяется по красному смещению,
интерпретируя его эффектом Допплера. Для малых
для удаляющихся галактик.
Скорость удаления галактики определяется по красному смещению,
интерпретируя его эффектом Допплера. Для малых ![]()
Первое измерение постоянной Хаббла (см. пример современной Хаббловской диаграммы на Рис. 10.1)
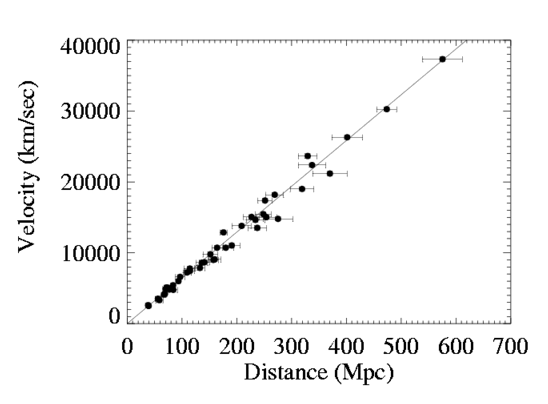 |
| Рис. 10.1
Хаббловская диаграмма (зависимость скорости удаления
(в км/с),
измеренной по красному смещению, от расстояния (в Мпк)) для
сверхновых типа 1а. Тангенс угла наклона
прямой, аппроксимирующей эту зависимость, дает современное значение
постоянной Хаббла |
1933, Ф. Цвикки, скрытая масса в скоплениях галактик
1949, Алфер, Бете, Гамов - гипотеза "горячей Вселенной"
("Big Bang") и предсказание существования изотропного реликтового
излучения с равновесным спектром с температурой ![]() K
1965, А. Пензиас, Р. Вилсон - открытие изотропного космического микроволнового
фона (реликтовое излучение) с температурой около 3 К.
K
1965, А. Пензиас, Р. Вилсон - открытие изотропного космического микроволнового
фона (реликтовое излучение) с температурой около 3 К.
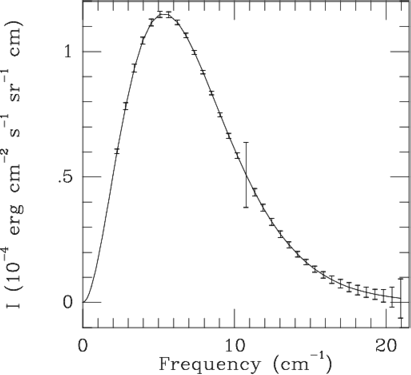 |
| Рис. 10.2 Спектр космического микроволнового (реликтового) излучения. Сплошная кривая - функция Планка для абсолютно черного тела с температурой Т=2.728 К. |
1979-80, А. Гус, А.А. Старобинский, А.Д. Линде, Д.А. Киржниц - гипотеза
"инфляционной" (раздувающейся) Вселенной
1992-1993, в космических экспериментах "Реликт" (Россия),
"COBE" (США) обнаружены флюктуации реликтового
излучения на уровне
![]() в масштабах
около 10 градусов.
1998, Хаббловские диаграммы (зависимость видимая
звездная величина в максимуме блеска - красное смещение)
для Сверхновых типа Iа (термоядерные
взрывы белых карликов с массой вблизи предела Чандрасекара)
показывают, что на больших расстояниях расширение Вселнной происходит
с ускорением. Это указывает неизбежность введения положительной
космологической постоянной (Эйнштейн, 1917) или более
сложного вида материи (т.н. темной энергии" или "квинтэссенции")
с уравнением состояния
в масштабах
около 10 градусов.
1998, Хаббловские диаграммы (зависимость видимая
звездная величина в максимуме блеска - красное смещение)
для Сверхновых типа Iа (термоядерные
взрывы белых карликов с массой вблизи предела Чандрасекара)
показывают, что на больших расстояниях расширение Вселнной происходит
с ускорением. Это указывает неизбежность введения положительной
космологической постоянной (Эйнштейн, 1917) или более
сложного вида материи (т.н. темной энергии" или "квинтэссенции")
с уравнением состояния
![]() , которая дает максимальный вклад в современную
плотность
энергии Вселенной (
, которая дает максимальный вклад в современную
плотность
энергии Вселенной (![]() ) и эффективно создает антигравитацию на больших
масштабах.
2000, измерение углового спектра флюктуаций реликтового
микроволнового излучения в экспериментах
BOOMERanG и MAXIMA. Открытие первого допплеровского пика в
угловом спектре флюктуаций на масштабах около 1 градуса,
предсказанного А.Д. Сахаровым в 1967 г. (т.н. "Сахаровские
колебания"). Доказательство плоской (Евклидовой) геометрии
пространственных сечений наблюдаемой Вселенной
с точностью порядка 10% до красных смещений
) и эффективно создает антигравитацию на больших
масштабах.
2000, измерение углового спектра флюктуаций реликтового
микроволнового излучения в экспериментах
BOOMERanG и MAXIMA. Открытие первого допплеровского пика в
угловом спектре флюктуаций на масштабах около 1 градуса,
предсказанного А.Д. Сахаровым в 1967 г. (т.н. "Сахаровские
колебания"). Доказательство плоской (Евклидовой) геометрии
пространственных сечений наблюдаемой Вселенной
с точностью порядка 10% до красных смещений ![]() (эпоха рекомбинации) (Рис. 10.3 и 10.4).
(эпоха рекомбинации) (Рис. 10.3 и 10.4).
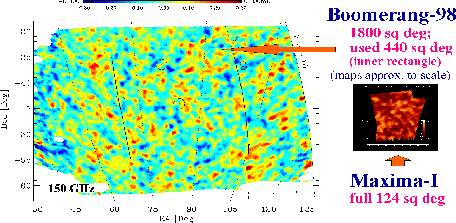 |
| Рис. 10.3 Карта флюктуаций космического микроволнового излучения в масштабах от 5 угловых минут до нескольких градусов по данным эксперимента BOOMERanG (карта слева) и МАХIMA (карта справа). |
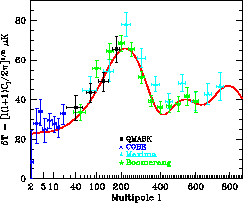 |
| Рис. 10.4
Угловой спектр флюктуаций
реликтового излучения по данным экспериментов BOOMERanG, MAXIMA и QMASK.
Положение первого пика на |
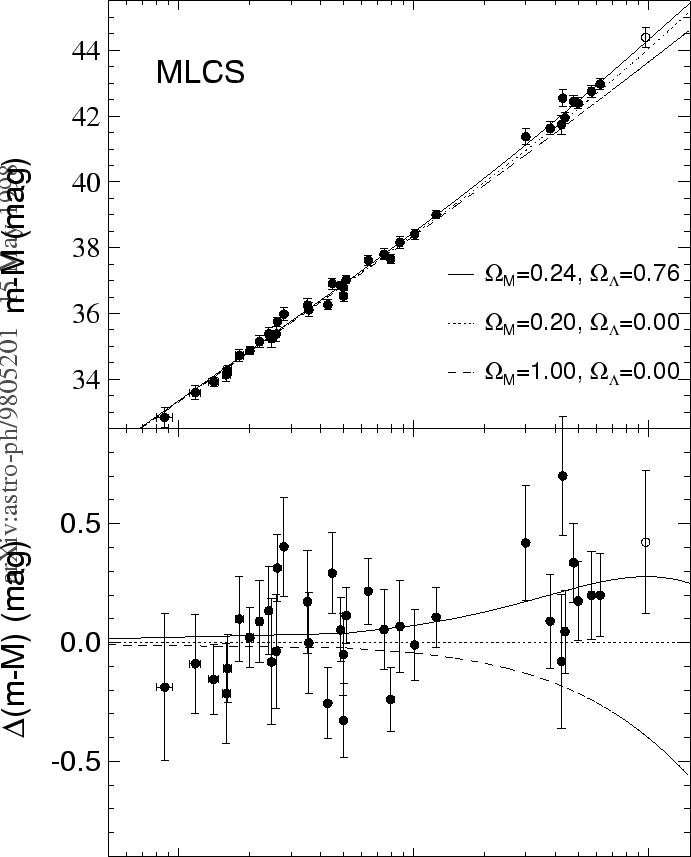 |
| Рис. 10.5 Хаббловская диаграмма видимая звездная величина - красное смещение для SN Ia, свидетельствующая об ускоренном расширении Вселенной в настоящее время (т.е. о преобладани положительной космологической постоянной в современной динамике Вселенной). В нижней части рисунка приведена разница в модуле расстояния (видимая величина - абсолютная величина) для различных космологических моделей. [Из работы A. Riess et al. 1998, AJ 116, 1009]. |
Несмотря на колоссальный прогресс в современной космологии, много важных вопросов оcтаются нерешенными :
- Проблема небарионной скрытой массы (наблюдаемое вещество
во Вселенной составляет по массе не более нескольких процентов
от полной массы тяготеющего вещества)
- Проблема космологической постоянной (или почему не
видна огромная энергия нулевых флюктуаций вакуума ?)
и примыкающая к ней проблема "квинтэссенции" (субстанции
неизвестной природы, не показывающей гравитационного скучивания и
имеющей уравнение состояния
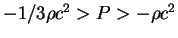 ),
создающей в настоящее время антигравитацияю в больших
масштабах и делающих Вселенную практически плоской
),
создающей в настоящее время антигравитацияю в больших
масштабах и делающих Вселенную практически плоской
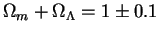 )
)
- Самая ранняя Вселенная (квантовое рождение, стрела
времени, космология на 3-мерной бране в многомерном пространстве
и т.д.)
10.1.3 Закон Хаббла
.Сначала рассмотрим простейшие однородные и изотропные космологические модели без космологической постоянной. В силу однородности возьмем в пространстве ограниченную сферическую область и проследим за ее эволюцией. Внешние области несущественны, т.к. поле тяготения, создаваемое веществом вне сферы (при строгой сферической симметрии) тождественно равно нулю (Толмен 1934, доказательство в рамках ОТО).
Замечание.
В ньютоновской теории тяготение описывается уравнением
![]() , и внутри полой сферы
, и внутри полой сферы
![]() , а ньютонова теория локально
является точной: для слабого гравитационного поля или в любой
достаточно малой окрестности сколь угодно сильного
гравитационного поля можно
пространство-время рассматривать как плоское, с метрикой
, а ньютонова теория локально
является точной: для слабого гравитационного поля или в любой
достаточно малой окрестности сколь угодно сильного
гравитационного поля можно
пространство-время рассматривать как плоское, с метрикой
![]() , где
, где
![]() -
метрика плоского пространства-времени Минковского,
-
метрика плоского пространства-времени Минковского, ![]() - малые
возмущения метрики; для перехода к ньютоновскому гравпотенциалу
- малые
возмущения метрики; для перехода к ньютоновскому гравпотенциалу
![]() можно пользоваться разложением
можно пользоваться разложением
![]() ,
,
![]() .
.
Как следует из астрономических наблюдений спектров галактик,
скорость их удаления от наблюдателя прямо пропорциональна расстоянию:
Рассмотрим массу, заключенную внутри выделенного шара радиуса ![]() :
:
![]() . Изменение плотности при расширении
. Изменение плотности при расширении
10.1.4 Закон эволюции. Критическая плотность
Рассмотрим точку на границе области,
расширяющейся по закону (10.1).
Уравнение движения
Заметим, что ни масса, ни радиус шара в уравнения не вошли, следовательно можем распространить рассмотрение на большие области (однако лишь до тех пор, пока применима Ньютонова гравитация).
Умножая (10.3) на ![]() и интегрируя,
получаем закон сохранения энергии
и интегрируя,
получаем закон сохранения энергии
где
есть так называемя критическая плотность в момент
Замечания.
1). Так как в настоящее время ![]() (красное
смещение - Вселенная расширяется!), первое слагаемое
(красное
смещение - Вселенная расширяется!), первое слагаемое ![]() возрастает с уменьшением
возрастает с уменьшением ![]() , а значит в прошлом скорость расширения была
больше (т.е. расширение должно замедляться - очевидное свойство
движения с учетом тормозящего действия гравитации), и в рассматриваемой
модели в прошлом был момент
такой, что
, а значит в прошлом скорость расширения была
больше (т.е. расширение должно замедляться - очевидное свойство
движения с учетом тормозящего действия гравитации), и в рассматриваемой
модели в прошлом был момент
такой, что
![]() и
и ![]() (сингулярность).
Итак, прошлое целиком определяется поведением первого слагаемого
2) Будущее: целиком определяется знаком второго слагаемого (константа
в законе сохранения энергии), т.е. соотношением
(сингулярность).
Итак, прошлое целиком определяется поведением первого слагаемого
2) Будущее: целиком определяется знаком второго слагаемого (константа
в законе сохранения энергии), т.е. соотношением
![]() :
А) Если
:
А) Если
![]() (
(![]() ) - второе слагаемое отрицательное,
расширение тормозится и сменяется сжатием (т.к. первое слагаемое
) - второе слагаемое отрицательное,
расширение тормозится и сменяется сжатием (т.к. первое слагаемое
![]() при
при ![]() ) - модель "закрытой Вселенной",
полная энергия Вселенной положительна;
В)
) - модель "закрытой Вселенной",
полная энергия Вселенной положительна;
В) ![]() , второе слагаемое положительно, и расширение продолжается
вечно с асимптотической скоростью
, второе слагаемое положительно, и расширение продолжается
вечно с асимптотической скоростью
![]() при
при ![]() - модель открытой Вселенной, полная энергия
Вселенной отрицательна;
C)
- модель открытой Вселенной, полная энергия
Вселенной отрицательна;
C) ![]() , расширение продолжается неограниченно,
в пределе с асимптотически
стремящейся к нулю скоростью. Полная энергия равна нулю
(кинетическая энергия в любой момент времени точно компенсируется
потенциальной энергией)10.1.
3). Современные наблюдения (Хаббловские диаграммы
для сверхновых типа 1а) интерпретируются как указание на
ускоренное расширение Вселенной. Это можно объяснить, введя
в модель силы отталкивания, действующие на больших расстояниях.
Именно такой физический эффект оказывает
положительная космологическая постоянная, введенная А.Эйнштейном
в 1917 г. для получения стационарных решений ОТО в применении ко
всей Вселенной.
, расширение продолжается неограниченно,
в пределе с асимптотически
стремящейся к нулю скоростью. Полная энергия равна нулю
(кинетическая энергия в любой момент времени точно компенсируется
потенциальной энергией)10.1.
3). Современные наблюдения (Хаббловские диаграммы
для сверхновых типа 1а) интерпретируются как указание на
ускоренное расширение Вселенной. Это можно объяснить, введя
в модель силы отталкивания, действующие на больших расстояниях.
Именно такой физический эффект оказывает
положительная космологическая постоянная, введенная А.Эйнштейном
в 1917 г. для получения стационарных решений ОТО в применении ко
всей Вселенной.
Подчеркнем еще раз, что приведенные выше рассуждения относились к моделям
Фридмана без космологической постоянной. Введение космологической
постоянной меняет картину качественно: наблюдаемое сегодня
ускореное расширение Вселенной означает увеличение постоянной Хаббла
со временем. Однако в прошлом обязательно должен быть
момент, когда масштабный фактор ![]() увеличивался с замедлением. Важно, что до этого момента
(например, в ранней Вселенной)
космологическая
постоянная не играла динамической роли.
увеличивался с замедлением. Важно, что до этого момента
(например, в ранней Вселенной)
космологическая
постоянная не играла динамической роли.
10.1.4.1 Продолжительность расширения и "Возраст Вселенной"
Продолжим рассмотрение фридмановских моделей без космологической
постоянной.
Закон Хаббла
![]() имеет простую геометрическую
интерпретацию: тангенс угла наклона касательной к кривой
имеет простую геометрическую
интерпретацию: тангенс угла наклона касательной к кривой ![]() в точке
в точке ![]() есть
есть ![]() , то есть время от момента пересечения
касательной оси времени
, то есть время от момента пересечения
касательной оси времени ![]() до момента
до момента ![]() :
:
![]() лет. На самом деле, реальный возраст меньше (зависит от
конкретного вида функции
лет. На самом деле, реальный возраст меньше (зависит от
конкретного вида функции ![]() )
)
10.1.4.2 Важный частный случай
В этом случае константа в уравнении энергии точно равна нулю,
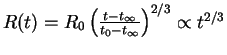 ,
,
для плотности: из
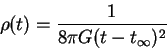
Замечание: в уравнении (10.6) 2-й член
10.1.5 Влияние давления
До сих пор мы рассматривали пыль или газ низкой плотности
с давлением ![]() (хорошее приближение для современной
стадии расширения). Для
обычного вещества
(хорошее приближение для современной
стадии расширения). Для
обычного вещества
![]() (
(
![]() - плотность
энергии), для релятивистских частиц (фотоны, нейтрино),
у которых энергия пропорциональна импульсу
- плотность
энергии), для релятивистских частиц (фотоны, нейтрино),
у которых энергия пропорциональна импульсу ![]() (точное равенство в случае безмассовых частиц)
(точное равенство в случае безмассовых частиц)
![]() . Для обычного вещества плотность падает как куб
масштабного фактора,
. Для обычного вещества плотность падает как куб
масштабного фактора,
![]() . Для релятивистских
частиц (излучения) при адиабатическом расширении плотность падает
быстрее, т.к. уменьшается плотность фотонов в единице объема (
. Для релятивистских
частиц (излучения) при адиабатическом расширении плотность падает
быстрее, т.к. уменьшается плотность фотонов в единице объема (![]() ) и уменьшается энергия каждого фотона (красное смещение)
(
) и уменьшается энергия каждого фотона (красное смещение)
(![]() ), поэтому
), поэтому
![]() .
Формальный вывод этого соотношения
следует из 1 закона термодинамики: если
есть давление, оно совершает работу над соседними элементами
.
Формальный вывод этого соотношения
следует из 1 закона термодинамики: если
есть давление, оно совершает работу над соседними элементами
![]() , для излучения
, для излучения ![]() , откуда
, откуда
![]() . Поскольку для излучения в термодинамическом
равновесии (АЧТ)
. Поскольку для излучения в термодинамическом
равновесии (АЧТ) ![]() , температура
в расширяющейся Вселенной падает обратно пропорционально масштабному
фактору:
, температура
в расширяющейся Вселенной падает обратно пропорционально масштабному
фактору: ![]() , что, впрочем, очевидно: с точностью до
констант энергия = частота = температура, а значит
температура эволюционирует так же, как и частота, т.е. пропорционально
красному смещению.
, что, впрочем, очевидно: с точностью до
констант энергия = частота = температура, а значит
температура эволюционирует так же, как и частота, т.е. пропорционально
красному смещению.
Эти простые рассуждения показывают, что
уходя в прошлое, мы должны рано или поздно начать
учитывать влияние давления ![]() . Как было показано Толменом,
в рамках ОТО учет давления сводится к
замене плотности на сумму плотности энергии и утроенного давления:
. Как было показано Толменом,
в рамках ОТО учет давления сводится к
замене плотности на сумму плотности энергии и утроенного давления:
Тогда уравнение движения модифицируется в
Рассмотрим случай доминирования излучения, т.е. эпоху, когда плотность
энергии целиком определяется излучением. Тогда ![]() ,
,
![]() , где
, где ![]() некоторая постоянная.
Уравнение энергии при этом становится
некоторая постоянная.
Уравнение энергии при этом становится
При малых
при
<< 10. Космология | Оглавление | 10.2 Модели Фридмана с >>