|
Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд http://www.astronet.ru/db/msg/1169513/node52.html |
<< 8. Введение в ОТО | Оглавление | 8.2 Параллельный перенос векторов >>
8.1 Идея искривленного пространства-времени
Все тела независимо от их массы падают с одинаковым ускорением -- это было известно со времен Галилея. Но именно этот факт стал определяющим для Эйнштейна при создании общей теории относительности (ОТО). Закон тяготения Ньютона очень похож на закон Кулона. Однако в закон Ньютона в качестве гравитационного заряда входит величина, пропорциональная инертной массе. Почему же тяготения связано с инертной массой? С точки зрения ньютоновской теории это некоторая случайность. Однако именно от этого оттолкнулся Эйнштейн, когда ему пришла в голову идея искривленного пространства.
В плоском четырехмерном пространстве (
![]() ) движению по прямой соответствует
равномерное прямолинейное движение. В плоском пространстве прямая -- это кратчайшее
расстояние между двумя точками, т. е. экстремаль. Идея Эйнштейна заключается в том, что
и в поле тяготения все тела движутся по экстремальным (геодезическим) линиям в
пространстве-времени, которое, однако, уже не плоское, а искривленное. Пространство-время
искривляют массы, создающие поле тяжести. Если пространство искривлено, и все тела движутся
по геодезическим, то это означает, что тела разной природы будут двигаются по одинаковым траекториям, т. е.
естественно объясняется независимость ускорения свободного падения от природы тела.
) движению по прямой соответствует
равномерное прямолинейное движение. В плоском пространстве прямая -- это кратчайшее
расстояние между двумя точками, т. е. экстремаль. Идея Эйнштейна заключается в том, что
и в поле тяготения все тела движутся по экстремальным (геодезическим) линиям в
пространстве-времени, которое, однако, уже не плоское, а искривленное. Пространство-время
искривляют массы, создающие поле тяжести. Если пространство искривлено, и все тела движутся
по геодезическим, то это означает, что тела разной природы будут двигаются по одинаковым траекториям, т. е.
естественно объясняется независимость ускорения свободного падения от природы тела.
Что такое искривленное пространство? Проще всего это понять на примере двумерного
случая. Рассмотрим поверхность шара
![]() . ``Прямыми'' на этой поверхности будут
дуги большого круга, так как им соответствуют кратчайшие расстояния на поверхности. Сумма углов
треугольника уже не равна
. ``Прямыми'' на этой поверхности будут
дуги большого круга, так как им соответствуют кратчайшие расстояния на поверхности. Сумма углов
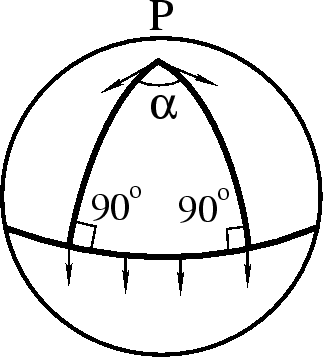
треугольника уже не равна ![]() . Рассмотрим треугольник с вершиной в полюсе и двумя
вершинами на экваторе (рис. 51).
Сумма углов в этом треугольнике равна
. Рассмотрим треугольник с вершиной в полюсе и двумя
вершинами на экваторе (рис. 51).
Сумма углов в этом треугольнике равна
![]() .
Площадь треугольника равна
.
Площадь треугольника равна
![]() .
.
В двумерном случае можно представить кривое пространство вложенным в трехмерное
пространство. Однако пространство данной размерности можно изучать и непосредственно, по
внутренним свойствам, не обращаясь к идее вложения. Например, точки поверхности шара
можно характеризовать двумя независимыми координатами ![]() и
и ![]() (широтой и долготой).
Можно найти выражение для элемента длины на поверхности шара
(широтой и долготой).
Можно найти выражение для элемента длины на поверхности шара
Для элемента длины в плоском двумерном пространстве можно записать
Итак, отличие кривой поверхности от плоской можно обнаружить, исследуя геометрию самой двумерной поверхности, без вложения.
Обратимся к трехмерному случаю.
В плоском пространстве квадрат элемента длины ![]() между двумя бесконечно близкими
точками записывается в виде (
между двумя бесконечно близкими
точками записывается в виде (
![]() -- соответствующие разности координат)
-- соответствующие разности координат)
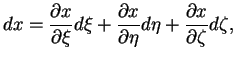
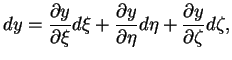
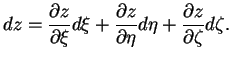
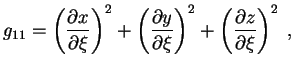
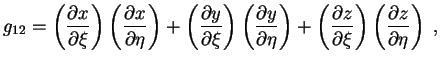
Пока мы только лишь в новом виде описали плоское пространство. Имеем 9 величин
![]() , из которых только 6 независимы, так как
, из которых только 6 независимы, так как
![]() . Можно показать,
что в плоском пространстве сами величины
. Можно показать,
что в плоском пространстве сами величины ![]() , их первые и вторые производные
определенным образом связаны. Уместен вопрос, что будет, если выбрать
, их первые и вторые производные
определенным образом связаны. Уместен вопрос, что будет, если выбрать ![]() ,
чтобы эти связи не выполнялись? Тогда окажется, что такая метрика описывает
искривленное пространство, которое уже трудно представить наглядно.
При этом
,
чтобы эти связи не выполнялись? Тогда окажется, что такая метрика описывает
искривленное пространство, которое уже трудно представить наглядно.
При этом ![]() определяют как координатную сетку, так и кривизну пространства.
определяют как координатную сетку, так и кривизну пространства.
Здесь уместно сделать историческое замечание: Лобачевский и Больяи рассматривали пространство, кривизна которого везде постоянна. Не выражая этой мысли в явном виде, они исходили из идеи, что существуют абсолютно жесткие тела. Такое тело может перемещаться в пространстве постоянной кривизны.
Характеризуя пространство метрическими коэффициентами ![]() , являющимися произвольными функциями
координат, Риман ввел в рассмотрение пространство, кривизна которого меняется от точки к точке.
В этот же период возникают первые идеи о том, что кривизна пространства может быть
связана с физическими факторами. Отказ от идеи абсолютно жесткого тела стал вполне естественным
позже, с развитием электронной теории и открытием лоренцева сокращения тел.
, являющимися произвольными функциями
координат, Риман ввел в рассмотрение пространство, кривизна которого меняется от точки к точке.
В этот же период возникают первые идеи о том, что кривизна пространства может быть
связана с физическими факторами. Отказ от идеи абсолютно жесткого тела стал вполне естественным
позже, с развитием электронной теории и открытием лоренцева сокращения тел.
В искривленном пространстве можно определять кривую, дающую минимум расстояния между двумя точками:
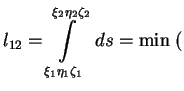 по всем путям
из 1 в 2
по всем путям
из 1 в 2В общем случае искривленного пространства такой простой зависимости не будет; можно написать только дифференциальные уравнения -- уравнения геодезической.
Наконец, следующий шаг заключается в том, что рассматривается как исходное, четырехмерное пространство Минковского, или, другими словами, комплекс, состоящий из времени и трехмерного пространства (в узком смысле слова).
Это четырехмерное многообразие преобразуется по Лоренцу, а не по Галилею, т. е. так, что остается инвариантным
<< 8. Введение в ОТО | Оглавление | 8.2 Параллельный перенос векторов >>