Астронет > 7. Новые физические факторы. Механическая устойчивость звезд

Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд
http://www.variable-stars.ru/db/msg/1169513/node46.html

Физические основы строения и эволюции звезд

<< 6.7 Качественная картина эволюции | Оглавление | 7.2 Нейтронизация >>

7. Новые физические факторы. Механическая устойчивость звезд

Разделы

7.1 Общая теория относительности -- ОТО

Везде выше мы пользовались ньютоновской теорией тяготения, условие применимости которой $\vert\varphi \vert\ll c^2$ . Введем пока формально понятие гравитационного радиуса -- величины, при которой параболическая скорость убегания с поверхности становится равной в рамках ньютоновской теории:

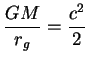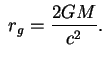
$\displaystyle {GM\over {r_g}}={c^2\over 2}\;$ откуда $\displaystyle \;r_g={2GM\over{c^2}}.$

Численно $r_g=3\cdot 10^5\;(M/M_\odot)$ .

Качественно эффекты ОТО можно учесть следующим образом: там, где в ньютоновской теории сила тяжести пропорциональна , в ОТО эта сила $\sim GM/(R(R-r_g))$ , т.е. сила тяготения обращается в бесконечность на . Найдем теперь величину средней плотности, при которой эффекты ОТО становятся важными:

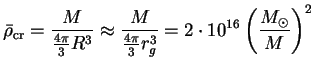$\displaystyle \bar{\rho}_{\rm cr}={M\over {{4\pi\over 3}R^3}}\approx{M\over {{4\pi\over 3}r_g^3}}=2\cdot 10^{16}\left({M_\odot\over M}\right)^2\;$ г/см $\displaystyle ^3.$

Отсюда вывод: чем больше масса, тем при меньшей плотности достигаются релятивистские эффекты. Например, для квазаров $M\sim 10^8\;M_\odot$ они становятся важны при $\bar{\rho}_{\rm cr}\sim 1\;$ г/см

, т.е. вещество локально находится в обычном состоянии, а релятивистские эффекты появляются просто из-за того, что его много. Для обычных звезд $\bar{\rho}_{\rm cr}\sim 10^{16}\;$ г/см

, и здесь сначала будут проявлять себя специфические эффекты вещества (нейтронизация, диссоциация ядер и пр.).

<< 6.7 Качественная картина эволюции | Оглавление | 7.2 Нейтронизация >>