Astronet Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд
http://variable-stars.ru/db/msg/1169513/node22.html
Физические основы строения и эволюции звезд
<< 3.3 Кинетика фотонов и | Оглавление | 3.5 Рассеяние излучения на ... >>

3.4 Тормозное излучение зарядов

Заряд (электрон), движущийся равномерно и прямолинейно, очевидно, ничего не излучает (чтобы в этом убедиться, достаточно перейти в систему отсчета, где он покоится). Из классической электродинамики известно, что количество энергии, излучаемой зарядом в единицу времени, определяется его ускорением:

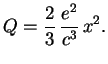
$\displaystyle Q={2\over 3}\,{e^2\over c^3}\,x^2. $

Подчеркнем, что эта формула относится к одному заряду. Если ускоряются два жестко связанных электрона, то $ Q$ возрастает в 4 раза (так как $ Q\sim e^2$). Таким образом, нельзя просто суммировать $ Q$ от различных зарядов.

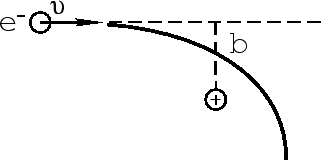
Ниже мы будем рассматривать излучение электрона при ускорении его во внешнем электрическом поле, скажем, в кулоновском поле иона. Вдали электрон движется практически с постоянной скоростью. Ускорение электрона максимально при пролете на минимальном расстоянии от иона. Очевидно, при этом максимально и излучение. Нас будет интересовать и спектральный состав излучения $ Q_\nu\simeq e^2x_\nu^2/c ^3$, где $ x_\nu$ -- фурье-компонента ускорения.

Займемся излучением длинных волн. Фурье-компонента ускорения

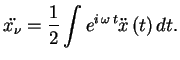
$\displaystyle \ddot {x_\nu}={1\over 2}\int e^{i\,\omega\,t}\ddot x\,(t)\,dt. $

Если $ \vert\omega t\vert<1$ (длинные волны)

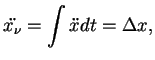
$\displaystyle \ddot {x_\nu}=\int \ddot xdt=\Delta x, $

т.е. $ \ddot {x_\nu}$ равно изменению скорости за время полета и не зависит от $ \nu$. Тогда при одном столкновении в единичном интервале частот излучается энергия

$\displaystyle Q_\nu\,\left[{\mbox{эрг}\over \mbox{Гц}}\right]={4\over 3}\,e^2\,{(\Delta x)^2\over c^3}.$ (3.3)

Подчеркнем еще раз, что это выражение справедливо только при $ \omega<1/\tau$, где $ \tau$ -- длительность события (столкновения) (рассматриваем длинные волны). Заметим, что размерность $ Q_\nu$ в формуле (3.3) изменилась на с$ ^2$ по сравнению с размерностью $ Q\,\left[{\mbox{эрг}\over \mbox{с}}\right]$, так как мы перешли сначала на единичный интервал частот и, кроме того, рассматриваем энергию, излученную не в секунду, а за все время пролета.

\begin{wrapfigure}{l}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f18.ai}\hss} \end{wrapfigure}
Рис. 18.

Легко подсчитать изменение импульса электрона, пролетающего в поле иона, первоначально имеющего скорость $ v$ и прицельный параметр $ b$ (рис. 18):

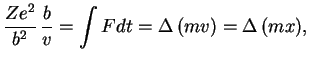
$\displaystyle {Ze^2\over b^2}\,{b\over v}=\int Fdt=\Delta\,(mv)=\Delta\,(mx), $

откуда

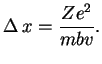
$\displaystyle \Delta\,x={Ze^2\over {mbv}}. $

Пусть на ион с бесконечности падает пучок электронов со скоростью $ v$ и плотностью $ N_e$. Через кольцо площадью $ 2\pi bdb$ около поля иона проходит $ N_ev2\pi bdb$ электронов в секунду. Каждый из них в единичном интервале частот излучает $ Q_\nu$. Если в 1 см$ ^3$ находится $ N_Z$ ионов, то полный поток энергии, излучаемый в единицу времени, очевидно, равен интегралу (логарифмический множитель опускаем)

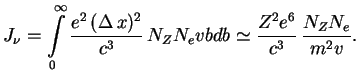
$\displaystyle J_\nu=\int\limits_0^\infty {e^2\,(\Delta\,x)^2\over c^3}\,N_ZN_evbdb\simeq {Z^2e^6\over c^3}\,{N_ZN_e\over {m^2v}}. $

Из квантовой механики известно, что квант частотой $ \nu$ может излучить только электрон, имеющий энергию больше $ mv_{min}^2/2=h\nu$. Поэтому в полное выражение войдет множитель $ e^{-h\nu/kT}$

$\displaystyle J_\nu={32\pi\over 3}\,{\left({2\pi\,m\over {3kT}}\right)}^{1/2}\,... ...^{-{h\nu\over {kT}}}\;\left[{\mbox{эрг}\over {\mbox{см}^3 \mbox{с Гц}}}\right] $

(формула тормозного или $ ff$-излучения). В этой формуле учтено, что электроны имеют максвелловское распределение по скоростям с температурой $ T$. Как видим, число квантов с $ h\nu>kT$ экспоненциально мало. Это связано с тем, что большие кванты излучаются электронами с большими энергиями, сосредоточенными в ``хвосте'' максвелловского распределения.

При данном объемном коэффициенте $ J_\nu$ изменение интенсивности $ F_\nu$ в прозрачной среде, очевидно, определяется уравнением

$\displaystyle (n\nabla\,F_\nu)={dF_\nu\over {dx}}={J_\nu\over {4\pi}}, $

где $ x$ -- координата вдоль произвольного направления $ n$. Прозрачный источник ( малы поглощение и индуцированное излучение) дает одну и ту же освещенность в любой точке сферы с радиусом много больше размеров источника независимо от формы источника. В общем случае с учетом индуцированного излучения и поглощения изменение интенсивности вдоль определенного направления выражается уравнением

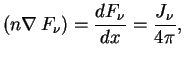
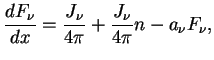
$\displaystyle {dF_\nu\over {dx}}={J_\nu\over {4\pi}}+{J_\nu\over {4\pi}}n-a_\nu F_\nu, $

где $ a_\nu\;[$см$ ^{-1}]$ -- коэффициент поглощения.

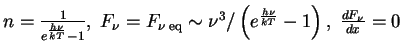При полном термодинамическом равновесии $ n={1\over {e^{h\nu\over {kT}}-1}},\;F_ \nu=F_{\nu\;\rm eq}\sim \nu^3/\left({e^{h\nu\over {kT}}-1}\right),\;{dF_\nu\over {dx}}=0$. Получаем, что отношение объемного коэффициента излучения вещества $ J_\nu$ к его коэффициенту поглощения $ a_\nu$ есть универсальная функция $ \nu$ и $ T$ (закон Кирхгофа):

$\displaystyle J_\nu/a_\nu=8\pi\,h\,\nu^3\,e^{-{h\nu\over {kT}}}/c^2. $

Таким образом, если вычислено $ J_\nu$, то $ a_\nu$ находится элементарно, и для свободно-свободных $ (ff)$-переходов получаем

$\displaystyle a_\nu={4\over 3}\,{\left({2\pi\over {3kTm}}\right)}^{1\over 2}\,{... ...{hcm\,\nu^3}}={3,7\cdot 10^8Z^2N_ZN_e\over {\nu^3\sqrt{T}}}\;[\mbox{см}^{-1}]. $

Объединим в правой части уравнения переноса члены, отвечающие индуцированному излучению и поглощению, так как оба они пропорциональны неизвестной функции координат -- интенсивности излучения $ F_\nu$ (поскольку $ n\sim F_\nu$). В члене индуцированного испускания $ J_\nu n/4\pi$ выразим $ J_\nu$ через коэффициент поглощения $ a_\nu$, тогда правая часть примет вид $ {J_\nu\over 4\pi}-a_\nu(1-e^{-{h\nu\over kT}})\,F_\nu$.

Отсюда видно, что вынужденное испускание можно трактовать как некое уменьшение поглощения: часть квантов как бы поглощается и тут же испускается с той же частотой и в том же направлении с вероятностью $ e^{-h\nu/kT}$. Физически такие акты никак себя не проявляют и их можно вообще исключить из рассмотрения, вводя

$\displaystyle a'_\nu=a_\nu\,(1-e^{-{h\nu\over kT}}). $

Уравнение переноса принимает вид

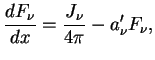
$\displaystyle {dF_\nu\over dx}={J_\nu\over 4\pi}-a'_\nu F_\nu, $

и взаимодействие излучения с веществом можно представить так, как будто существует только спонтанное испускание и эффективное поглощение, описываемое коэффициентом $ a'_\nu$.

Коэффициент истинного поглощения $ a_\nu\sim \nu^{-3}$, но при $ h\nu<kT$ эффективное поглощение $ a'_\nu\sim \nu^{-2}$ и в равновесии это дает рэлей-джинсовскую формулу для интенсивности $ F_{\rm eq}\sim {J_\nu\over a'_\nu}\sim\nu^2$ (коэффициент излучения $ I_\nu$ при $ h\nu<kT$ фактически постоянен). Используя закон Кирхгофа $ {J_\nu\over 4\pi}=a'_\nu F_{\nu\;\rm eq}$, запишем в общем случае уравнение переноса в виде

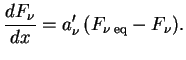
$\displaystyle {dF_\nu\over dx}=a'_\nu\,(F_{\nu\;\rm eq}-F_\nu). $

Это уравнение записано для координаты, изменяющейся вдоль луча зрения. Из него видно, что, если при $ x=0\;F_\nu=0$, то сначала, при малых $ x<1/a'_\nu,\;F_\nu$ стремится к $ F_{\nu\;\rm eq}$ линейно: $ F_\nu=a'_\nu F_{\nu\;\rm eq}x$, а затем при $ x>1 /a'_\nu$ быстро устанавливается равновесие, при котором $ F_\nu=F_{\nu\;\rm eq}$. Если размеры излучающего облака (слоя) $ x_0$ меньше $ 1/a'_\nu$, то оно является оптически тонким и интенсивность его излучения всегда меньше равновесной в $ a'_\nu x_0$ раз. Полный поток энергии, излучаемой такими облаками, пропорционален $ F=\int F_\nu d\nu= x_o\,\int a'_\nu F_{\nu\;\rm eq}d\nu$. Введем средний коэффициент поглощения

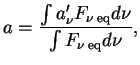
$\displaystyle a={\int a'_\nu F_{\nu\;\rm eq}d\nu\over \int F_{\nu\;\rm eq}d\nu}, $

тогда

$\displaystyle F=ax_0F_{eq}. $

Средний коэффициент поглощения для тормозного механизма, очевидно, равен

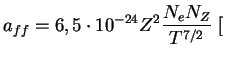$\displaystyle a_{ff}=6,5\cdot 10^{-24}Z^2{N_eN_Z\over T^{7/2}}\;[$см$\displaystyle ^{-1}]. $

Соответствующая средняя длина свободного пробега фотона

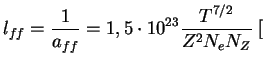$\displaystyle l_{ff}={1\over a_{ff}}=1,5\cdot 10^{23}{T^{7/2}\over Z^2N_eN_Z}\;[$см$\displaystyle ]. $

Причем, если плазма содержит смесь ионов с зарядами $ Z_i$ и атомными массами $ A_i$, то

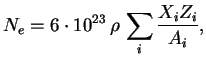
$\displaystyle N_e=6\cdot 10^{23}\,\rho\,\sum\limits_i{X_iZ_i\over A_i}, $

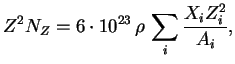
$\displaystyle Z^2N_Z=6\cdot 10^{23}\,\rho\,\sum\limits_i{X_iZ_i^2\over A_i}, $

где $ X_i$ -- весовая доля данного иона.

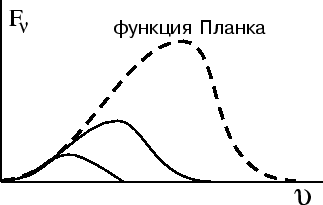
\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f19.ai}\hss} \end{wrapfigure}
Рис. 19.

Рассмотрим процесс установления равновесия между веществом и излучением для однородной неограниченной среды, в которой в начальный момент $ t=0$ излучение отсутствовало, а вещество было мгновенно нагрето до температуры $ T_0$. Очевидно, что прежде всего это равновесие установится на низких частотах, так как $ a'_\nu\sim 1/\nu^2$. С течением времени равновесие будет устанавливаться при больших значениях $ \nu$ (см. рис. 19).


<< 3.3 Кинетика фотонов и | Оглавление | 3.5 Рассеяние излучения на ... >>

Rambler's Top100 Яндекс цитирования