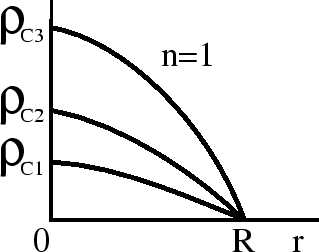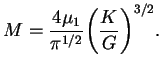|
Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд http://www.astronet.ru/db/msg/1169513/node15.html |
<< 2.2 Основные параметры политропы | Оглавление | 2.4 Теория белых карликов >>
2.3 Частные случаи политропных моделей
1. ![]() . Как видно из выше приведенной таблицы, при
. Как видно из выше приведенной таблицы, при ![]() безразмерный радиус
безразмерный радиус
![]() . Из формул для
. Из формул для
![]() видно, что конечные
значения энергий звезды совместимы с конечной массой только при
видно, что конечные
значения энергий звезды совместимы с конечной массой только при
![]() .
Решения уравнения Эмдена с
.
Решения уравнения Эмдена с ![]() вообще теряют обычный физический смысл.
вообще теряют обычный физический смысл.
Случай ![]() имеет аналитическое решение вида
имеет аналитическое решение вида
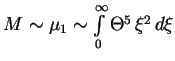 сходится на верхнем пределе. Полный момент инерции
сходится на верхнем пределе. Полный момент инерции
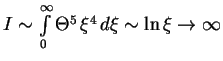 , но
, но
2. ![]() . Для давления в этом случае имеет место соотношение
. Для давления в этом случае имеет место соотношение
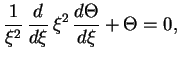
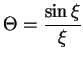
и обращается в нуль при ![]() . В силу линейности задачи радиус звезды
. В силу линейности задачи радиус звезды ![]() не зависит от массы. При данном
не зависит от массы. При данном ![]() величины
величины ![]() и
и ![]() пропорциональны
пропорциональны ![]() ,
и в один объем можно вложить (равновесно!) разное количество вещества. При
увеличении массы растет только центральная плотность
,
и в один объем можно вложить (равновесно!) разное количество вещества. При
увеличении массы растет только центральная плотность ![]() (рис. 13).
(рис. 13).
Задача. Получите этот результат из размерностных соображений. Учтите
при этом, что размерность ![]() зависит от индекса
зависит от индекса ![]() .
.
3. ![]() -- несжимаемая жидкость. Формально при
-- несжимаемая жидкость. Формально при ![]() из уравнения состояния
из уравнения состояния
![]() следует, что малые изменения
следует, что малые изменения ![]() дают большие изменения
дают большие изменения ![]() .
Это дает нам право отождествлять случай
.
Это дает нам право отождествлять случай ![]() с несжимаемой однородной жидкостью
с несжимаемой однородной жидкостью
![]() const
const![]() . Так как тепловая энергия
. Так как тепловая энергия ![]() равна работе, затраченной
на сжатие данного газового объема, в случае несжимаемой жидкости
равна работе, затраченной
на сжатие данного газового объема, в случае несжимаемой жидкости ![]() и,
следовательно,
и,
следовательно, ![]() . Это видно и из формулы
. Это видно и из формулы
![]() для
для ![]() . Полная энергия
. Полная энергия ![]() , очевидно, равна гравитационной
, очевидно, равна гравитационной ![]() .
.
4. ![]() . Случай
. Случай ![]() является наиболее интересным и физически важным. Как мы
увидим ниже, он осуществляется и в белых карликах, и в больших горячих звездах,
где
является наиболее интересным и физически важным. Как мы
увидим ниже, он осуществляется и в белых карликах, и в больших горячих звездах,
где
![]() (здесь
(здесь
![]() -- плотность
энергии
-- плотность
энергии
![]() эрг
эрг![]() см
см![]() ). И даже для Солнца наиболее близки к реальности
политропные модели с
). И даже для Солнца наиболее близки к реальности
политропные модели с ![]() .
.
В чем особенность этого случая? Во-первых, теория политропных шаров при данном
уравнении состояния (при данном ![]() ) и данной массе
) и данной массе ![]() не позволяет вычислить
радиус звезды. Кроме того, полная энергия звезды
не позволяет вычислить
радиус звезды. Кроме того, полная энергия звезды
![]() , т.е.
, т.е. ![]() .
.
Почему это происходит? Рассмотрим порядковые оценки. Тепловая энергия ![]() при
при ![]() по порядку равна
по порядку равна
![]() . Для гравитационной энергии
всегда имеем
. Для гравитационной энергии
всегда имеем
![]() . Полная энергия
. Полная энергия
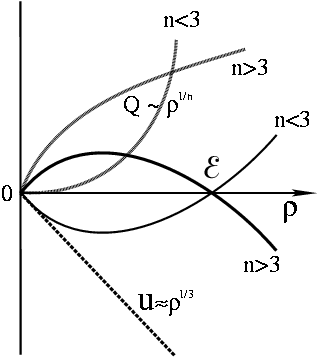
![]() . Очевидно, что для разных
. Очевидно, что для разных ![]() энергия
энергия ![]() по разному зависит от
по разному зависит от
![]() (рис. 14).
В любом случае зависимость
(рис. 14).
В любом случае зависимость
![]() линейная.
Очевидно, что при
линейная.
Очевидно, что при
![]() система при малых возмущениях начнет разлетаться
(
система при малых возмущениях начнет разлетаться
(![]() стремится уменьшиться), а при
стремится уменьшиться), а при
![]() будет неограниченно
сжиматься (коллапсировать). Равновесие возможно только при
будет неограниченно
сжиматься (коллапсировать). Равновесие возможно только при
![]() , для этого
случая имеется только одно определенное значение массы:
, для этого
случая имеется только одно определенное значение массы:
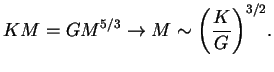
Таким образом, равновесная модель с ![]() имеет три важных свойства:
имеет три важных свойства:
1) равновесие возможно только при одном определенном значении массы (если ![]() фиксировано), 2) полная энергия
фиксировано), 2) полная энергия
![]() , 3) радиус звезды
, 3) радиус звезды ![]() может быть
любым, т.е. равновесие безразличное.
может быть
любым, т.е. равновесие безразличное.
Рассмотрим кратко, как ведет себя полная энергия ![]() в зависимости от
плотности при
в зависимости от
плотности при
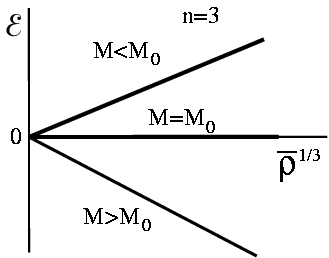
![]() (рис. 15). В случае
(рис. 15). В случае ![]() набор кривых для разных масс
имеет минимум, а при
набор кривых для разных масс
имеет минимум, а при ![]() максимум. Очевидно, что точки
максимум. Очевидно, что точки
![]() являются положениями равновесия, но при
являются положениями равновесия, но при ![]() это равновесие
устойчиво, а при
это равновесие
устойчиво, а при ![]() неустойчиво.
неустойчиво.
<< 2.2 Основные параметры политропы | Оглавление | 2.4 Теория белых карликов >>